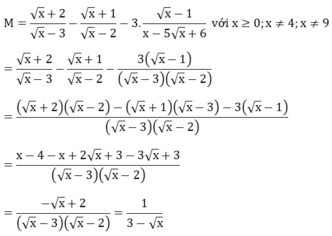tính, thu gọn (x-3)(x-6)+x(4-x)

Những câu hỏi liên quan
Thu gọn P
\(P=\dfrac{x-\sqrt{x}}{x-9}+\dfrac{1}{\sqrt{x}+3}-\dfrac{1}{\sqrt{x}-3}\)
a) Tính P biết \(x=\sqrt{6+4\sqrt{2}}+\sqrt{6-4\sqrt{2}}\)
b) Tính P biết \(x=\dfrac{1}{\sqrt{2}-1}-\dfrac{1}{\sqrt{2}+1}\)
Cho đa thức \(P(x) = 9{x^4} + 8{x^3} - 6{x^2} + x - 1 - 9{x^4}\).
a) Thu gọn đa thức P(x).
b) Tìm số mũ cao nhất của x trong dạng thu gọn của P(x).
a) \(P(x) = 9{x^4} + 8{x^3} - 6{x^2} + x - 1 - 9{x^4} = (9{x^4} - 9{x^4}) + 8{x^3} - 6{x^2} + x - 1 = 8{x^3} - 6{x^2} + x - 1\).
b) Số mũ cao nhất của x trong dạng thu gọn của P(x) là 3.
Đúng 0
Bình luận (0)
Thu gọn
\(\left(\dfrac{6x+4\sqrt{x}}{x\sqrt{x}-4\sqrt{x}}-\dfrac{6}{3\sqrt{x}+6}+1\right):\dfrac{1}{\sqrt{x}-2}\)
ĐKXĐ: \(\left\{{}\begin{matrix}x>0\\x\ne4\end{matrix}\right.\)
\(\left(\dfrac{6x+4\sqrt{x}}{x\sqrt{x}-4\sqrt{x}}-\dfrac{6}{3\sqrt{x}+6}+1\right):\dfrac{1}{\sqrt{x}-2}\)
\(=\left(\dfrac{2\sqrt{x}\left(3\sqrt{x}+2\right)}{\sqrt{x}\left(x-4\right)}-\dfrac{6}{3\left(\sqrt{x}+2\right)}+1\right):\dfrac{1}{\sqrt{x}-2}\)
\(=\left(\dfrac{2\left(3\sqrt{x}+2\right)}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}-\dfrac{2}{\sqrt{x}+2}+1\right):\dfrac{1}{\sqrt{x}-2}\)
\(=\dfrac{6\sqrt{x}+4-2\left(\sqrt{x}-2\right)+x-4}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}\cdot\dfrac{\sqrt{x}-2}{1}\)
\(=\dfrac{x+6\sqrt{x}-2\sqrt{x}+4}{\left(\sqrt{x}+2\right)}=\dfrac{\left(\sqrt{x}+2\right)^2}{\left(\sqrt{x}+2\right)}\)
\(=\sqrt{x}+2\)
Đúng 3
Bình luận (0)
thu gọn đa thức
a. 3x(x-5)-(x-2)7x
b. (x+4)(x-4)-2x(3-x)
c. (3x-7)(-2x+1)-8x(6-x)
a, 3x(x-5)-(x-2)7x
= 3x2 - 15x -7x2 - 14x
= -4x2 - 29x
= -x(4x+ 29)
b,(x+4)(x+4)-2x(3-x)
= x2 - 42 - 6x + 2x2
= 3x2 - 6x - 16
c,(3x-7)(-2x+1)-8x(6-x)
= -6x2 + 3x +14x -7 - 48x + 8x2
= 2x2 - 31x - 7
Đúng 0
Bình luận (0)
3: Thu gọn và sắp xếp các hạng tử của đa thức theo lũy thừa giảm dần của biển.
P(x) = x ^ 5 + 2x ^ 2 - x ^ 2 - 2x ^ 3 - x ^ 5 + x ^ 4 - 3x + 1
Q(x) = - x ^ 6 + 2x ^ 3 + 6 - 2x ^ 4 + x ^ 6 - x - 1 + 2x ^ 4
`P(x)=x ^ 5 + 2x ^ 2 - x ^ 2 - 2x ^ 3 - x ^ 5 + x ^ 4 - 3x + 1`
`P(x)= (x^5-x^5)+x^4-2x^3+(2x^2-x^2)-3x+1`
`P(x)=x^4+2x^3+x^2-3x+1`
`Q(x)=`\(-x^6+2x^3+6-2x^4+x^6-x-1+2x^4\)
`Q(x)= (-x^6+x^6)+(-2x^4+2x^4)+2x^3-x+(6-1)`
`Q(x)=2x^3-x+5`
Đúng 0
Bình luận (0)
1) Thu gọn và tìm bậc đa thức N = 2x mu 3 y mu 2 + x mu 3 y - 6 x mu 2 y - x mu 3 y mu 2 + 6 x mu 2 y + 3 x mu 3 y
2) Thu gọn và xác định bậc đa thức M = 4 phan 5 x mu 3 y mu 5 – 0,7xy + 2 phan 5 x mu 3 y mu 5 – xy + 1 phan 4 x mu 3 y mu 5
3) Thu gọn và tính giá trị đa thức tại x = -1, y = 1
Cho: A(x)=3+x^2+5x^4-2x^3+x^2+4x^4+2x^3-x
B(x)=-8x^4 + x - 5x^3 - 2x^2 + 4x^3 - x +3
1.Thu gọn và sắp xếp đa thức theo lũy thừa giảm dần của biến
2.Tính A(x)+B(x), A(x)-B(x) và tìm bậc của A(x)-B(x)
3.Chứng tỏ x=6 là nghiệm của P(x)=A(x)+B(x)-x^4+x^3
Mong mn giúp em với ạ.
1: A(x)=5x^4+4x^4+x^2+x^2-x+3
=9x^4+2x^2-x+3
B(x)=-8x^4-x^3-2x^2+3
2: A(x)+B(x)
=9x^4+2x^2-x+3-8x^4-x^3-2x^2+3
=x^4-x^3-x+6
A(x)-B(x)
=9x^4+2x^2-x+3+8x^4+x^3+2x^2-3
=17x^4+x^3+4x^2-x
bậc của A(x)-B(x) là 4
3: P(x)=x^4-x^3-x+6-x^4+x^3=-x+6
P(6)=-6+6=0
=>x=6 là nghiệm của P(x)
Đúng 0
Bình luận (0)
Bài 3: 1) Thu gọn và tìm bậc đa thức N = 2x3 y 2 + x3 y - 6 x2 y - x 3 y 2 + 6 x2 y + 3x3 y
2) Thu gọn và xác định bậc đa thức M = 4 5 x 3 y 5 – 0,7xy + 2 5 x 3 y 5 – xy + 1 4 x 3 y 5
3) Thu gọn và tính giá trị đa thức tại x = -1, y = 1
Đề lỗi rồi kìa, bạn viết lại đi tridung
Đúng 0
Bình luận (0)
Cho biểu thức:
M
x
+
2
x
-
3
+
x
+
1
x
-
2
-
3
.
x
-
1
x
-
5...
Đọc tiếp
Cho biểu thức:
M = x + 2 x - 3 + x + 1 x - 2 - 3 . x - 1 x - 5 x + 6 với x ≥ 0 , x ≠ 4 , x ≠ 9
a) Thu gọn biểu thức M.
Thu gọn rồi tính giá trị của đa thức một biến sau tại x=0x=0.
4x^{3}-4x^{2}-6 + 4x^{2}-2x^{3}+34x3−4x2−6+4x2−2x3+3
Đáp số: Giá trị của đa thức bằng: