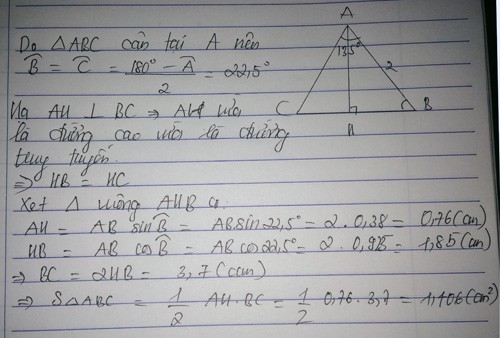cho tam giác ABC cân tại A có góc BAC=135 độ và AB=2 tính diện tích ABC

Những câu hỏi liên quan
Cho tam giác ABC cân tại A có góc BAC = 135 độ, AB = 2 cm. Tính diện tích tam giác ABC.
Cho tam giác ABC cân tại A có góc BAC = 135 độ và AB = 2 cm . Khi đó diện tích tam giác ABC ...
Cho tam giác ABC cân A có góc BAC =135 độ và AB=2cm. Tính diện tích tam giác ABC
cho tam giác ABC cân tại A , Góc BAC=135 độ , AB=2cm.Tính diện tích tam giác ABC.
Mk xin cách lm nha. Bn nào giải xog dc 3 tick nhé
Cho tam giác ABC có AC=3cm, góc BAC = 135 độ, Diện tích tam giác ABC là 6 cm. Tính độ dài cạnh AB
\(\dfrac{1}{2}\cdot AB\cdot AC\cdot sinA=6\)
=>1/2*3*sin135*AB=6
=>\(AB=4\sqrt{2}\left(cm\right)\)
Đúng 0
Bình luận (1)
Cho tam giác ABC cân tại A , Góc BAC=135 độ , AB=2cm.Tính diện tích tam giác ABC.
Cho tam giác ABC có AB=15cm, AC=20cm,BC=25cm. Đường phân giác góc BAC cắt BC tại D
a) tính độ dài DB và DC
b) tính tỉ số diện tích tam giác ABC và tam giác ACD
c)Cho tam giác ABC có diện tích bằng F tính diện tích tam giác ABD và diện tích tam giác ACD theo F
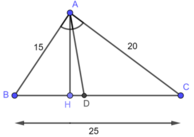
a) Trong tam giác ABC, ta có: AD là đường phân giác của:
⇒\(\dfrac{DB}{DC}\)=\(\dfrac{AB}{AC}\)
Mà AB = 15cm và AC = 20cm ( gt )
Nên \(\dfrac{DC}{DB}\)=\(\dfrac{15}{20}\)
⇒\(\dfrac{DB}{DB+DC}\)=\(\dfrac{15}{15+20}\)( Tính chất tỉ lệ thức đã học ở lớp 7 )
⇒\(\dfrac{DB}{BC}\)=\(\dfrac{15}{35}\)⇒DB=\(\dfrac{15}{35}\).BC=\(\dfrac{15}{35}\).25=\(\dfrac{75}{5}\)(cm)
b) Kẻ AH⊥BC
Ta có:\(S_{ABD}\)=\(\dfrac{1}{2}\)AH.BD
\(S_{ACD}\)=\(\dfrac{1}{2}\)AH.CD
⇒\(\dfrac{S_{ABD}}{S_{ACD}}\)=\(\dfrac{\dfrac{1}{2}AH.BD}{\dfrac{1}{2}AH.CD}\)=\(\dfrac{BD}{DC}\)
Mà \(\dfrac{DB}{DC}\)=\(\dfrac{15}{12}\)=\(\dfrac{3}{4}\)
⇒\(\dfrac{S_{ABD}}{S_{ACD}}\)=\(\dfrac{3}{4}\)(đpcm)
Đúng 0
Bình luận (0)
cho tam giác ABC cân tại Acó BAC = 135 độ và AB = 2cm. TÍnh Sabc = .......
AB=AC=2cm
SABC= \(\frac{1}{2}\sin\widehat{BAC}\cdot AB\cdot AC\)=\(\sqrt{2}\)
Đúng 0
Bình luận (0)
Cho tam giác cân ABC cân tại A. Tia phân giác của góc BAC cắt cạnh BCtại M.1) Chứng minh tam giác AMB tam giác AMC.2) a- Biết góc BAC 500. Tính góc ABC và góc ACB.b- Biết BC 6 cm; AM 4 cm. Tính độ dài AB, AC?3) Kẻ ME vuông góc AB tại E, MF vuông góc AC tại F. Chứng minh tam giác AEF cân.4) Kẻ EI vuông góc BC tại I. Gọi K là giao của đường thẳng EI và đường thẳng AC. Chứngminh A là trung điểm của đoạn KF.
Đọc tiếp
Cho tam giác cân ABC cân tại A. Tia phân giác của góc BAC cắt cạnh BC
tại M.
1) Chứng minh tam giác AMB = tam giác AMC.
2) a- Biết góc BAC = 500. Tính góc ABC và góc ACB.
b- Biết BC = 6 cm; AM = 4 cm. Tính độ dài AB, AC?
3) Kẻ ME vuông góc AB tại E, MF vuông góc AC tại F. Chứng minh tam giác AEF cân.
4) Kẻ EI vuông góc BC tại I. Gọi K là giao của đường thẳng EI và đường thẳng AC. Chứng
minh A là trung điểm của đoạn KF.
1: Xét ΔAMB và ΔAMC có
AB=AC
\(\widehat{BAM}=\widehat{CAM}\)
AM chung
Do đó:ΔAMB=ΔAMC
2:
a: \(\widehat{ABC}=\widehat{ACB}=\dfrac{180^0-50^0}{2}=65^0\)
b: BC=6cm nên BM=3cm
=>AB=AC=5cm
3: Xét ΔAEM vuông tại E và ΔAFM vuông tại F có
AM chung
\(\widehat{EAM}=\widehat{FAM}\)
Do đó: ΔAEM=ΔAFM
Suy ra: AE=AF
hay ΔAEF cân tại A
Đúng 2
Bình luận (1)