Ta có : |x - 2| ; |x - 5| ; |x - 18| ≥0∀x∈R≥0∀x∈R

=> |x - 2| + |x - 5| + |x - 18|  ≥0∀x∈R≥0∀x∈R

=> D có giá trị nhỏ nhất khi x = 2;5;18

Mà x ko thể đồng thời nhận 3 giá trị

Nên GTNN của D là : 16 khi x = 5   ok nha bạn

x^2/x-1 = x^2-4x+4/x-1 + 4 = (x-2)^1/x-1 + 4 >= 4

Dấu "=" xảy ra <=> x-2 = 0 <=> x = 2 (tm)

Vậy GTNN của x^2/x-1 = 4 <=> x= 2

k mk nha

TL

\(\frac{11}{4}\)

Xin k

Nhớ k

HT

ko hieu

1.

Đặt \(\frac{x}{3}=t\) pt trở thành:

\(cos4t=sin^23t\Leftrightarrow2cos4t=1-cos6t\)

\(\Leftrightarrow cos6t+2cos4t-1=0\)

\(\Leftrightarrow4cos^32t-3cos2t+2\left(2cos^22t-1\right)-1=0\)

\(\Leftrightarrow4cos^32t+2cos^22t-3cos2t-3=0\)

\(\Leftrightarrow\left(cos2t-1\right)\left(4cos^22t+6cos2t+3\right)=0\)

\(\Leftrightarrow cos2t=1\Leftrightarrow cos\frac{2x}{3}=1\)

\(\Leftrightarrow\frac{2x}{3}=k2\pi\Leftrightarrow x=k3\pi\)

2.

\(\Leftrightarrow4cos^3x-3cosx-\left(1-2sin^2x\right)+9sinx-4=0\)

\(\Leftrightarrow cosx\left(4cos^2x-3\right)+2sin^2x+9sinx-5=0\)

\(\Leftrightarrow cosx\left(4\left(1-sin^2x\right)-3\right)+\left(2sinx-1\right)\left(sinx+5\right)=0\)

\(\Leftrightarrow cosx\left(1-4sin^2x\right)+\left(2sinx-1\right)\left(sinx+5\right)=0\)

\(\Leftrightarrow\left(cosx+2sinx.cosx\right)\left(1-2sinx\right)-\left(1-2sinx\right)\left(sinx+5\right)=0\)

\(\Leftrightarrow\left(1-2sinx\right)\left(cosx-sinx+2sinx.cosx-5\right)=0\)

\(\Leftrightarrow\left(1-2sinx\right)\left(\sqrt{2}cos\left(x+\frac{\pi}{4}\right)+sin2x-5\right)=0\)

\(\Leftrightarrow1-2sinx=0\) (do \(\sqrt{2}cos\left(x+\frac{\pi}{4}\right)\le\sqrt{2};sin2x\le1\) nên ngoặc sau luôn âm)

\(\Leftrightarrow sinx=\frac{1}{2}\Rightarrow\left[{}\begin{matrix}x=\frac{\pi}{6}+k2\pi\\x=\frac{5\pi}{6}+k2\pi\end{matrix}\right.\)

[(-5)^10+2020][2^3(-5)-4(-10)

=[(-5)^10+2020].0

=0

nhớ đấy

nhớ đấy

nhớ chọn đấy

\(\dfrac{x-y}{x+y}=\dfrac{z-x}{z+x}\\ \Rightarrow\left(x-y\right)\left(z+x\right)=\left(x+y\right)\left(z-x\right)\\ \Rightarrow xz+x^2-yz-yx=xz-x^2+yz-yx\\ \Rightarrow xz-xz+x^2+x^2=yz+yz-yx+yx\\ \Rightarrow2x^2=2yz\\ \Rightarrow x^2=yz\)

a/

\(\Leftrightarrow2sinx.cosx+2\sqrt{3}cos^2x=\sqrt{3}-2sin5x\)

\(\Leftrightarrow sin2x+\sqrt{3}\left(cos2x+1\right)=\sqrt{3}-2sin5x\)

\(\Leftrightarrow sin2x+\sqrt{3}cos2x=-2sin5x\)

\(\Leftrightarrow\frac{1}{2}sin2x+\frac{\sqrt{3}}{2}cos2x=-sin5x\)

\(\Leftrightarrow sin\left(2x+\frac{\pi}{3}\right)=sin\left(-5x\right)\)

\(\Leftrightarrow\left[{}\begin{matrix}2x+\frac{\pi}{3}=-5x+k2\pi\\2x+\frac{\pi}{3}=\pi+5x+k2\pi\end{matrix}\right.\)

\(\Leftrightarrow\left[{}\begin{matrix}x=-\frac{\pi}{21}+\frac{k2\pi}{7}\\x=-\frac{2\pi}{9}+\frac{k2\pi}{3}\end{matrix}\right.\)

b/

\(\Leftrightarrow sinx+\sqrt{3}cosx=2sin3x+2sinx\)

\(\Leftrightarrow sinx-\sqrt{3}cosx=-2sin3x\)

\(\Leftrightarrow\frac{1}{2}sinx-\frac{\sqrt{3}}{2}cosx=-sin3x\)

\(\Leftrightarrow sin\left(x-\frac{\pi}{3}\right)=sin\left(-3x\right)\)

\(\Leftrightarrow\left[{}\begin{matrix}x-\frac{\pi}{3}=-3x+k2\pi\\x-\frac{\pi}{3}=\pi+3x+k2\pi\end{matrix}\right.\)

\(\Leftrightarrow\left[{}\begin{matrix}x=\frac{\pi}{12}+\frac{k\pi}{2}\\x=-\frac{2\pi}{3}+k\pi\end{matrix}\right.\)

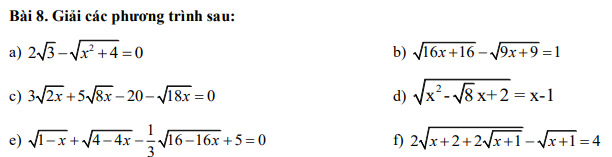
a.

$2\sqrt{3}-\sqrt{x^2+4}=0$

$\Leftrightarrow 2\sqrt{3}=\sqrt{x^2+4}$
$\Leftrightarrow 12=x^2+4$

$\Leftrightarrow 8=x^2$

$\Leftrightarrow x=\pm 2\sqrt{2}$

b. ĐKXĐ: $x\geq -1$

$\sqrt{16(x+1)}-\sqrt{9(x+1)}=1$

$\Leftrightarrow 4\sqrt{x+1}-3\sqrt{x+1}=1$

$\Leftrightarrow \sqrt{x+1}=1$
$\Leftrightarrow x+1=1$

$\Leftrightarrow x=0$ (tm)

c. ĐKXĐ: $x\geq 0$

$3\sqrt{2x}+5\sqrt{8x}-20-\sqrt{18x}=0$

$\Leftrightarrow 3\sqrt{2x}+10\sqrt{2x}-20-3\sqrt{2x}=0$

$\Leftrightarrow 10\sqrt{2x}-20=0$

$\Leftrightarrow \sqrt{2x}=2$
$\Leftrightarrow 2x=4$

$\Leftrightarrow x=2$ (tm)

d. 

PT \(\Rightarrow \left\{\begin{matrix} x-1\geq 0\\ x^2-\sqrt{8x}+2=(x-1)^2\end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} x\geq 1\\ x=\frac{1+\sqrt{2}}{2}\end{matrix}\right.\Leftrightarrow x=\frac{1+\sqrt{2}}{2}\)

e. ĐKXĐ: $x\leq 1$

PT $\Leftrightarrow \sqrt{1-x}+2\sqrt{1-x}-\frac{4}{3}\sqrt{1-x}+5=0$

$\Leftrightarrow \frac{5}{3}\sqrt{1-x}=-5< 0$ (vô lý)

Vậy pt vô nghiệm.

f. ĐKXĐ: $x\geq -1$

PT $\Leftrightarrow 2\sqrt{(\sqrt{x+1}+1)^2}-\sqrt{x+1}=4$

$\Leftrightarrow 2(\sqrt{x+1}+1)-\sqrt{x+1}=4$
$\Leftrightarrow \sqrt{x+1}=2$

$\Leftrightarrow x=3$ (tm)

a) Ta có: \(2\sqrt{3}-\sqrt{x^2+4}=0\)

\(\Leftrightarrow\sqrt{x^2+4}=2\sqrt{3}\)

\(\Leftrightarrow x^2+4=12\)

\(\Leftrightarrow x^2=8\)

hay \(x\in\left\{2\sqrt{2};-2\sqrt{2}\right\}\)

b) Ta có: \(\sqrt{16x+16}-\sqrt{9x+9}=1\)

\(\Leftrightarrow4\sqrt{x+1}-3\sqrt{x+1}=1\)

\(\Leftrightarrow\sqrt{x+1}=1\)

\(\Leftrightarrow x+1=1\)

hay x=0

Lời giải:

a. Để $f(x)=x^2-2mx+3m+4\geq 0$ với mọi $x\in\mathbb{R}$ thì:
\(\left\{\begin{matrix} a=1>0\\ \Delta'=m^2-3m-4\leq 0\end{matrix}\right.\Leftrightarrow m^2-3m-4\leq 0\)

$\Leftrightarrow (m+1)(m-4)\leq 0$

$\Leftrightarrow -1\leq m\leq 4$

b.

Để pt có 2 nghiệm pb cùng dấu thì:
\(\left\{\begin{matrix} \Delta'=m^2-3m-4>0\\ P=3m+4>0\end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} (m+1)(m-4)> 0\\ m> \frac{-4}{3}\end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} m> 4 \text{hoặc} m< -1\\ m> \frac{-4}{3}\end{matrix}\right.\)

$\Leftrightarrow m>4$ hoặc $\frac{-4}{3}< m < -1$

Lời giải:

a. Để $f(x)=x^2-2mx+3m+4\geq 0$ với mọi $x\in\mathbb{R}$ thì:
\(\left\{\begin{matrix} a=1>0\\ \Delta'=m^2-3m-4\leq 0\end{matrix}\right.\Leftrightarrow m^2-3m-4\leq 0\)

$\Leftrightarrow (m+1)(m-4)\leq 0$

$\Leftrightarrow -1\leq m\leq 4$

b.

Để pt có 2 nghiệm pb cùng dấu thì:
\(\left\{\begin{matrix} \Delta'=m^2-3m-4>0\\ P=3m+4>0\end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} (m+1)(m-4)> 0\\ m> \frac{-4}{3}\end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} m> 4 \text{hoặc} m< -1\\ m> \frac{-4}{3}\end{matrix}\right.\)

$\Leftrightarrow m>4$ hoặc $\frac{-4}{3}< m < -1$

Gọi chữ số hàng chục là x và chữ số hàng đơn vị là y (x;y là các chữ số từ 0 đến 9)

Do chữ số hàng chục hơn chữ số hàng đơn vị là 4

\(\Rightarrow x-y=4\)

Giá trị chữ số ban đầu: \(10x+y\)

Giá trị chữ số sau khi đổi chỗ: \(10y+x\)

Do tổng số mới và số cũ là 132 nên ta có pt:

\(10x+y+10y+x=132\Rightarrow11\left(x+y\right)=132\Rightarrow x+y=12\)

Ta được hệ: \(\left\{{}\begin{matrix}x-y=4\\x+y=12\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}x=8\\y=4\end{matrix}\right.\)

Vậy số đó là 84