cho hàm số y=f(x)=2x+1 và y=g(x)=\(x^2\)-4
tìm x biết g(x) = f(g(2))
a) Cho hàm số y=f(x)=-2x+3.Tính f(-2);f(-1);f(0);f(-1/2);f(1/2)
b) Cho hàm số y=g(x)=x^2-1.Tính g(-1);g(0);g(1);g(2)
a) Thay f(-2) vào hàm số ta có :
y=f(-2)=(-2).(-2)+3=7
Thay f(-1) vào hàm số ta có :
y=f(-1)=(-2).(-1)+3=5
Thay f(0) vào hàm số ta có :
y=f(0)=(-2).0+3=1
Thay f(-1/2) vào hàm số ta có :
y=f(-1/2)=(-2).(-1/2)+3=4
Thay f(1/2) vào hàm số ta có :
y=f(1/2)=(-2).1/2+3=2
b) Thay g(-1) vào hàm số ta có :
y=g(-1)=(-1)2-1=0
Thay g(0) vào hàm số ta có :
y=g(0)=02-1=-1
Thay g(1) vào hàm số ta có :
y=g(1)=12-1=0
Thay g(2) vào hàm số ta có :
y=g(2)=22-1=3
y ;jfjnvyh;fjjfy f,.hgdbn<hgy>33<-66475>
a) Thay f(-2) vào hàm số ta có :
y=f(-2)=(-2).(-2)+3=7
Thay f(-1) vào hàm số ta có :
y=f(-1)=(-2).(-1)+3=5
Thay f(0) vào hàm số ta có :
y=f(0)=(-2).0+3=1
Thay f(-1/2) vào hàm số ta có :
y=f(-1/2)=(-2).(-1/2)+3=4
Thay f(1/2) vào hàm số ta có :
y=f(1/2)=(-2).1/2+3=2
b) Thay g(-1) vào hàm số ta có :
y=g(-1)=(-1)2
-1=0
Thay g(0) vào hàm số ta có :
y=g(0)=0
2
-1=-1
Thay g(1) vào hàm số ta có :
y=g(1)=1
2
-1=0
Thay g(2) vào hàm số ta có :
y=g(2)=2
2
-1=3
chúc bn hok tốt @_@
Bài 1: Cho hàm số y =f( x)= -5x -1. Tính f(-1), f(0), f(1), f(1/2)
Bài 2: a) Cho hàm số y = f(x) = -2x + 3. Tính f(-2) ;f(-1) ; f(0) ; f(-1/2); f(1/2).
b) Cho hàm số y = g(x) = x – 1. Tính g(-1); g(0) ; g(1) ; g(2).
c) Với giá trị nào của x để hai hàm số trên nhận cùng giá trị
Lm giúp mình vs mình đang cần gấp .
Giải:
Bài 1: lần lượt thay các giá trị của x, ta có:
_Y=f(-1)= -5.(-1)-1=4
_Y=f(0)= -5.0-1=1
_Y=f(1)= -5.1-1=-6
_Y=f(1/2)= -5.1/2-1=-7/2
Bài 2:
a: f(-2)=7
f(-1)=5
f(0)=3
. a) Cho hàm số y = f(x) = -2x + 3. Tính f(-2) ;f(-1) ; f(0) ; f( 1 2 ); f( 1 2 ). b) Cho hàm số y = g(x) = x 2 – 1. Tính g(-1); g(0
giúp e với ạ
a: f(-2)=4+3=7
f(-1)=2+3=5
f(0)=3
f(1/2)=-1+3=2
f(-1/2)=1+3=4
b: g(-1)=1-1=0
f(0)=0-1=-1
a) Cho hàm số y=f(x)=-2x+3.Tính f(-2);f(-1);f(0);f(-1/2);f(1/2)
b) Cho hàm số y=g(x)=x^2-1.Tính g(-1);g(0);g(1);g(2)
c)Với giá trị nào của x để hai hàm số trên nhận cùng giá trị
Làm bài c thôi ạ mấy câu còn lại nháp thôi ạ.
Cho hàm số y= F(x) = x×(x-2) và hàm số y= G(x) = -x+6
a) tính F(3); [ F(2/3) ]² ; G(-1/2)
b) tìm x để F(x)=0
c) tìm a để F(a)=G(a)
a: \(F\left(3\right)=3\left(3-2\right)=3\cdot1=3\)
\(\left[F\left(\dfrac{2}{3}\right)\right]^2=\left[\dfrac{2}{3}\cdot\left(\dfrac{2}{3}-2\right)\right]^2\)
\(=\left[\dfrac{2}{3}\cdot\dfrac{-4}{3}\right]^2=\left(-\dfrac{8}{9}\right)^2=\dfrac{64}{81}\)
\(G\left(-\dfrac{1}{2}\right)=-\left(-\dfrac{1}{2}\right)+6=6+\dfrac{1}{2}=\dfrac{13}{2}\)
b: F(x)=0
=>x(x-2)=0
=>\(\left[{}\begin{matrix}x=0\\x-2=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=0\\x=2\end{matrix}\right.\)
c: F(a)=G(a)
=>\(a\left(a-2\right)=-a+6\)
=>\(a^2-2a+a-6=0\)
=>\(a^2-a-6=0\)
=>(a-3)(a+2)=0
=>\(\left[{}\begin{matrix}a-3=0\\a+2=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}a=3\\a=-2\end{matrix}\right.\)
Cho hàm số y = f ( x ) có đạo hàm trên ℝ . Xét các hàm số g ( x ) = f x − f 2 x và h ( x ) = f ( x ) − f ( 4 x ) . Biết rằng g ' ( 1 ) = 18 và g ' ( 2 ) = 1000 . Tính h ' ( 1 ) :
A. − 2018
.
B. 2018
C. 2020
D. − 2020
Cho hàm số y = f(x) có đạo hàm liên tục trên R đồ thị hàm số y = f’(x) như hình vẽ.
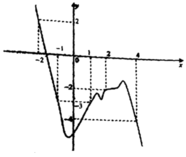
Biết f(2) = –6, f(–4) = –10 và hàm số g(x) = f(x)+ x 2 2 , g(x) có ba điểm cực trị.
Phương trình g(x) = 0?
A. Có đúng 2 nghiệm
B. Vô nghiệm
C. Có đúng 3 nghiệm
D. Có đúng 4 nghiệm
Đáp án B
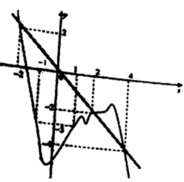
Phương pháp: Lập bảng biến thiên của g(x) và đánh giá số giao điểm của đồ thị hàm số y = g(x) và trục hoành.
Cách giải: 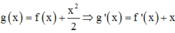
![]()
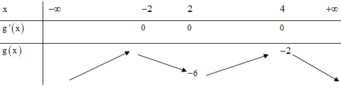
Xét giao điểm của đồ thị hàm sốy = f’(x) và đường thẳng y = -x ta thấy, hai đồ thị cắt nhau tại ba điểm có hoành độ là: -2;2;4 tương ứng với 3 điểm cực trị của y = g(x).
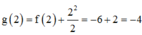
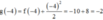
Bảng biến thiên:
Dựa vào bảng biến thiên ta thấy ![]() => phương trình g(x) = 0 không có nghiệm
=> phương trình g(x) = 0 không có nghiệm ![]()
Cho hàm số \(f\left( x \right) = 2x - \sin x,g\left( x \right) = \sqrt {x - 1} \).
Xét tính liên tục hàm số \(y = f\left( x \right).g\left( x \right)\) và \(y = \frac{{f\left( x \right)}}{{g\left( x \right)}}\).
• Xét hàm số \(f\left( x \right) = 2x - \sin x\) có tập xác định \(D = \mathbb{R}\).
Vậy hàm số \(f\left( x \right)\) liên tục trên \(\mathbb{R}\).
• Xét hàm số \(g\left( x \right) = \sqrt {x - 1} \)
ĐKXĐ: \(x - 1 \ge 0 \Leftrightarrow x \ge 1\)
Hàm số \(g\left( x \right) = \sqrt {x - 1} \) có tập xác định \(D = \left[ {1; + \infty } \right)\).
Hàm số \(g\left( x \right) = \sqrt {x - 1} \) là hàm căn thức nên liên tục trên khoảng \(\left( {1; + \infty } \right)\).
Ta có: \(\mathop {\lim }\limits_{x \to {1^ + }} g\left( x \right) = \mathop {\lim }\limits_{x \to {1^ + }} \sqrt {x - 1} = \sqrt {1 - 1} = 0 = g\left( 1 \right)\)
Do đó hàm số \(g\left( x \right) = \sqrt {x - 1} \) liên tục tại điểm \({x_0} = 1\).
Vậy hàm số \(g\left( x \right) = \sqrt {x - 1} \) liên tục trên nửa khoảng \(\left[ {1; + \infty } \right)\).
• Xét hàm số \(y = f\left( x \right).g\left( x \right) = \left( {2x - \sin x} \right)\sqrt {x - 1} \)
Do hàm số \(y = f\left( x \right)\) và \(y = g\left( x \right)\) đều liên tục tại mọi điểm \({x_0} \in \left[ {1; + \infty } \right)\) nên hàm số \(y = f\left( x \right).g\left( x \right)\) liên tục trên nửa khoảng \(\left[ {1; + \infty } \right)\).
• Xét hàm số \(y = \frac{{f\left( x \right)}}{{g\left( x \right)}} = \frac{{2x - \sin x}}{{\sqrt {x - 1} }}\)
Do hàm số \(y = f\left( x \right)\) và \(y = g\left( x \right)\) đều liên tục tại mọi điểm \({x_0} \in \left[ {1; + \infty } \right)\) nên hàm số \(y = \frac{{f\left( x \right)}}{{g\left( x \right)}}\) liên tục trên khoảng \(\left( {1; + \infty } \right)\).
Cho hàm y=f(x)=6-4x và y =g(x)= 2x2 -3x
Tính f(1); f=1/2; g=-2 và g = 2/3
Ta có :+)\(f\left(x\right)=6-4x\)
\(\implies\)\(f\left(1\right)=6-4=2\)
Ta có :+) \(f\left(x\right)=6-4x=\frac{1}{2}\)
\(\implies\) \(x=\frac{11}{8}\)
Ta có :+) \(g\left(x\right)=2x^2-3x\)
\(\implies\) \(g\left(-2\right)=2.\left(-2\right)^2+3.2\)
\(\implies\) \(g\left(-2\right)=4.2+3.2\)
\(\implies\) \(g\left(-2\right)=14\)