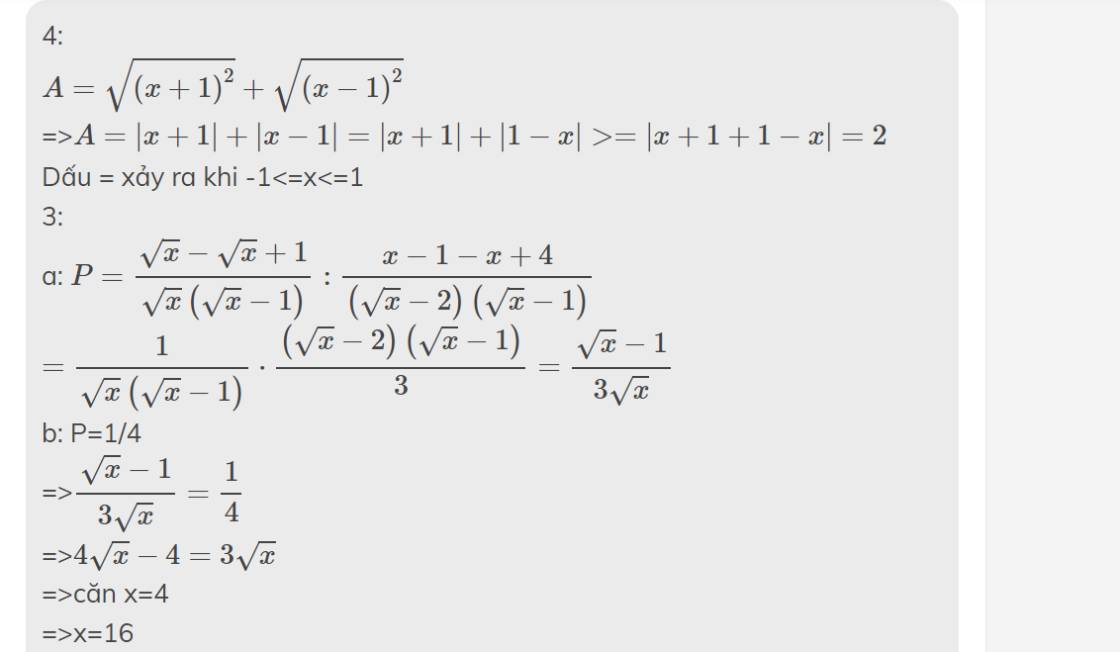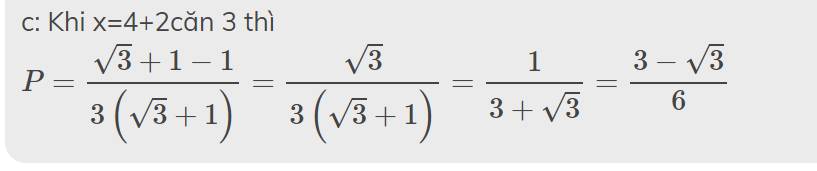3 câu gì?

c: Xét tứ giác AEHF có 

\(\widehat{EAF}=\widehat{AFH}=\widehat{AEH}=90^0\)

Do đó: AEHF là hình chữ nhật

Suy ra: AH=EF; AE=HF và AF=HE

Xét ΔAHB vuông tại H có HE là đường cao ứng với cạnh huyền AB

nên \(EA\cdot EB=HE^2\)

hay \(EA\cdot HF=HE^2\)

Xét ΔAHC vuông tại H có HF là đường cao ứng với cạnh huyền AC

nên \(FA\cdot FC=HF^2\)

hay \(FC\cdot HE=HF^2\)

Xét ΔEHF vuông tại H có 

\(EF^2=HF^2+HE^2\)

hay \(AH^2=EB\cdot HF+FC\cdot HE\)

Bài 1:

a) \(\sqrt{2x+6}\) có nghĩa khi:

\(2x+6\ge0\)

\(\Leftrightarrow2x\ge-6\)

\(\Leftrightarrow x\ge-3\)

b) \(\sqrt{\dfrac{-2}{2x-3}}\) có nghĩa khi:

\(\left\{{}\begin{matrix}\dfrac{-2}{2x-3}\ge0\\2x-3\ne0\end{matrix}\right.\)

\(\Leftrightarrow\left\{{}\begin{matrix}2x-3\le0\left(\text{vì: }-2< 0\right)\\2x\ne3\end{matrix}\right.\)

\(\Leftrightarrow\left\{{}\begin{matrix}x\le\dfrac{3}{2}\\x\ne\dfrac{3}{2}\end{matrix}\right.\)

\(\Leftrightarrow x< \dfrac{3}{2}\)

Bài 2:

a) \(\sqrt{\left(1+2\sqrt{3}\right)^2}-5\sqrt{3}\)

\(=1+2\sqrt{3}-5\sqrt{3}\)

\(=1-3\sqrt{3}\)

b) \(3\sqrt{2}+4\sqrt{8}-\sqrt{18}\)

\(=3\sqrt{2}+4\cdot2\sqrt{2}-3\sqrt{2}\)

\(=8\sqrt{2}\)

c) \(\dfrac{1}{3+\sqrt{2}}+\dfrac{1}{3-\sqrt{2}}\)

\(=\dfrac{3-\sqrt{2}}{\left(3+\sqrt{2}\right)\left(3-\sqrt{2}\right)}+\dfrac{3+\sqrt{2}}{\left(3+\sqrt{2}\right)\left(3-\sqrt{2}\right)}\)

\(=\dfrac{3-\sqrt{2}+3+\sqrt{2}}{9-2}\)

\(=\dfrac{6}{7}\)

- Không có hoàn vị gen: 50% DGHf : 50% DgHf

- Hoán vị gen 40%: 30% DGhf : 30% DgHf : 20% DGHf :20% Dghf

Đặt a/b=c/d=k

=>a=bk; c=dk

\(\dfrac{2a+3c}{a}=\dfrac{2bk+3dk}{bk}=\dfrac{2b+3d}{b}\)

a: ĐKXĐ: n+1<>0

=>n<>-1

b: Để A nguyên thì n+1-3 chia hết cho n+1

=>\(n+1\in\left\{1;-1;3;-3\right\}\)

=>\(n\in\left\{0;-2;2;-4\right\}\)

c: \(A=\dfrac{n+1-3}{n+1}=1-\dfrac{3}{n+1}\)
n>-1

Để A nhỏ nhất thì n+1=1

=>n=0

=>A min=1-3/1=-2