Chứng minh: \(cos5x.sin3x+sin7x.sinx=cos2x.cos4x\)

Những câu hỏi liên quan
2 sin7x.sinx + cos8x + \(\sqrt{3}\)sin6x = 1.
\(\Leftrightarrow cos6x-cos8x+cos8x+\sqrt{3}sin6x=1\)
\(\Leftrightarrow\frac{\sqrt{3}}{2}sin6x+\frac{1}{2}cos6x=\frac{1}{2}\)
\(\Leftrightarrow sin\left(6x+\frac{\pi}{3}\right)=sin\left(\frac{\pi}{6}\right)\)
\(\Leftrightarrow\left[{}\begin{matrix}6x+\frac{\pi}{3}=\frac{\pi}{6}+k2\pi\\6x+\frac{\pi}{3}=\frac{5\pi}{6}+k2\pi\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}x=-\frac{\pi}{36}+\frac{k\pi}{3}\\x=\frac{\pi}{12}+\frac{k\pi}{3}\end{matrix}\right.\)
Đúng 0
Bình luận (0)
1) giải pt:
a) cosx.cosx=cos2x.cos4x
b) cos5x.sin4x=cos3x.sin2x
c) sinx+sin2x=cosx+cos2x
d) sin2x+sin4x=sin6x
a/ Bạn coi lại vế trái đề bài, nhìn không hợp lý
b/ \(\Leftrightarrow\frac{1}{2}sin9x-\frac{1}{2}sinx=\frac{1}{2}sin5x-\frac{1}{2}sinx\)
\(\Leftrightarrow sin9x=sin5x\)
\(\Leftrightarrow\left[{}\begin{matrix}9x=5x+k2\pi\\9x=\pi-5x+k2\pi\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\frac{k\pi}{2}\\x=\frac{\pi}{14}+\frac{k\pi}{7}\end{matrix}\right.\)
c/ \(\Leftrightarrow sin2x-cos2x=cosx-sinx\)
\(\Leftrightarrow\sqrt{2}sin\left(2x-\frac{\pi}{4}\right)=\sqrt{2}cos\left(x+\frac{\pi}{4}\right)\)
\(\Leftrightarrow cos\left(\frac{3\pi}{4}-2x\right)=cos\left(x+\frac{\pi}{4}\right)\)
\(\Leftrightarrow\left[{}\begin{matrix}\frac{3\pi}{4}-2x=x+\frac{\pi}{4}+k2\pi\\\frac{3\pi}{4}-2x=-x-\frac{\pi}{4}+k2\pi\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\frac{\pi}{6}+\frac{k2\pi}{3}\\x=\pi+k2\pi\end{matrix}\right.\)
Đúng 0
Bình luận (1)
d/
\(\Leftrightarrow sin2x=sin6x-sin4x\)
\(\Leftrightarrow2sinx.cosx=2cos5x.sinx\)
\(\Leftrightarrow sinx\left(cosx-cos5x\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}sinx=0\\cos5x=cosx\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=k\pi\\5x=x+k2\pi\\5x=-x+k2\pi\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=k\pi\\x=\frac{k\pi}{2}\\x=\frac{k\pi}{3}\end{matrix}\right.\) \(\Leftrightarrow\left[{}\begin{matrix}x=\frac{k\pi}{2}\\x=\frac{k\pi}{3}\end{matrix}\right.\)
Đúng 0
Bình luận (0)
Bài 7: Cho ABC nhọn có các đường cao AD,BE,CF cắt nhau tại H.
a. Chứng minh AB.AF=AC.AE
b. Chứng minh AEF ABC.
c. Chứng minh Góc BEF=BCF
d. Chứng minh BH.BE+CH.CF=BC2.
e. Chứng minh EH là phân giác
g. Chứng minh : AF/FB.DB/DC.CE/EA=1
1.Chứng minh hai góc bằng nhau
2.Chứng minh hai đương thẳng vuông góc
3.Chứng minh hai đường thẳng song song
4.Chứng minh ba điểm thẳng hàng
5.Chứng minh một tia là tia phân giác
6.Chứng minh đoạn thẳng trung trực
7.Chứng minh hai tam giác băng nhau
8.Chứng minh một tam giác là tam giác đặc biệt
a) Chứng minh tam giác ABC tam giác AEDb)Chứng minh: góc BAC góc EAD c)Chứng minh tam giác ABD tam giác AECd)Cho I là trung điểm của CD, chứng minh tam giác ACI tam giác ADIe)Chứng minh: AI là phân giác của góc CADf)Chứng minh: AI là phân giác của góc BAEg)Chứng minh Ai vuông góc BE
Đọc tiếp
a) Chứng minh tam giác ABC = tam giác AED
b)Chứng minh: góc BAC = góc EAD
c)Chứng minh tam giác ABD = tam giác AEC
d)Cho I là trung điểm của CD, chứng minh tam giác ACI = tam giác ADI
e)Chứng minh: AI là phân giác của góc CAD
f)Chứng minh: AI là phân giác của góc BAE
g)Chứng minh Ai vuông góc BE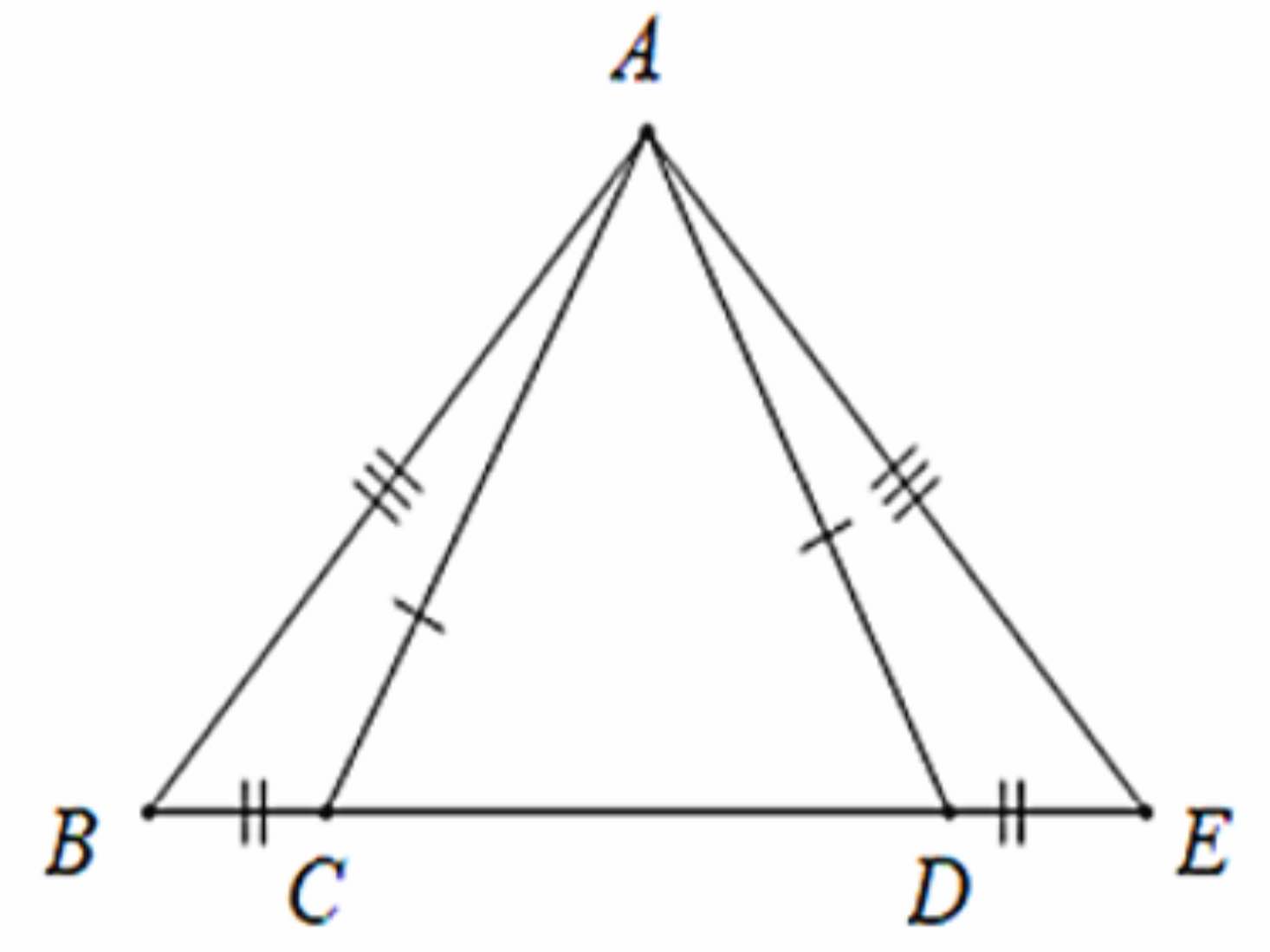
Cho hình chóp SABCD, đáy ABCD là hình vuông, SA vuông ABCD.
a) chứng minh rằng: CD vuông (SAD)
b) chứng minh: BC vuông (SAB)
c) chứng minh: AB vuông (SAD)
d) chứng minh: AD vuông (SAB)
e) chứng minh: BD vuông (SAC)
a: Ta có: CD\(\perp\)AD(ABCD là hình vuông)
CD\(\perp\)SA(SA\(\perp\)(ABCD))
AD,SA cùng thuộc mp(SAD)
Do đó: CD\(\perp\)(SAD)
b: Ta có: BC\(\perp\)AB(ABCD là hình vuông)
BC\(\perp\)SA(SA\(\perp\)(ABCD))
AB,SA cùng thuộc mp(SAB)
Do đó: BC\(\perp\)(SAB)
c: AB\(\perp\)AD(ABCD là hình vuông)
AB\(\perp\)SA(SA\(\perp\)(ABCD))
AD,SA cùng thuộc mp(SAD)
Do đó: AB\(\perp\)(SAD)
d: AD\(\perp\)AB
AD\(\perp\)SA(SA\(\perp\)(ABCD)))
SA,AB cùng thuộc mp(SAB)
Do đó: AD\(\perp\)(SAB)
e: BD\(\perp\)AC(ABCD là hình vuông)
BD\(\perp\)SA(SA\(\perp\)(ABCD))
AC,SA cùng thuộc mp(SAC)
Do đó: BD\(\perp\)(SAC)
Đúng 1
Bình luận (0)
Cho tam giác ABC. M là trung điểm AC.Trên tia đối của tia MB lấy điểm D sao cho BMMD.al Chứng minh : tam giác ABM tam giác CDMb/ Chứng minh : AB CDb/ Chứng minh : AB // CDd/ Chứng minh : tam giác AMD tam giác ACMBel Chứng minh ADBCf/ Chứng minh AD // BCg/ Trên DC kéo dài lấy điểm N sao cho CD CN (C ko bằng N) chứng minh : BN // AC.
Đọc tiếp
Cho tam giác ABC. M là trung điểm AC.Trên tia đối của tia MB lấy điểm D sao cho BM=MD.
al Chứng minh : tam giác ABM = tam giác CDM
b/ Chứng minh : AB = CD
b/ Chứng minh : AB // CD
d/ Chứng minh : tam giác AMD =tam giác ACMB
el Chứng minh AD=BC
f/ Chứng minh AD // BC
g/ Trên DC kéo dài lấy điểm N sao cho CD =CN (C ko bằng N) chứng minh : BN // AC.
Cho tam giác ABC. M là trung điểm AC.Trên tia đối của tia MB lấy điểm D sao cho BMMD.al Chứng minh : tam giác ABM tam giác CDMb/ Chứng minh : AB CDb/ Chứng minh : AB // CDd/ Chứng minh : tam giác AMD tam giác ACMBel Chứng minh ADBCf/ Chứng minh AD // BCg/ Trên DC kéo dài lấy điểm N sao cho CD CN (C ko bằng N) chứng minh : BN // AC.Ai đó giúp e với:((((((((
Đọc tiếp
Cho tam giác ABC. M là trung điểm AC.Trên tia đối của tia MB lấy điểm D sao cho BM=MD.
al Chứng minh : tam giác ABM = tam giác CDM
b/ Chứng minh : AB = CD
b/ Chứng minh : AB // CD
d/ Chứng minh : tam giác AMD =tam giác ACMB
el Chứng minh AD=BC
f/ Chứng minh AD // BC
g/ Trên DC kéo dài lấy điểm N sao cho CD =CN (C ko bằng N) chứng minh : BN // AC.
Ai đó giúp e với:((((((((
Cho tam giác ABC. M là trung điểm AC.Trên tia đối của tia MB lấy điểm D sao cho BMMD.al Chứng minh : tam giác ABM tam giác CDMb/ Chứng minh : AB CDb/ Chứng minh : AB // CDd/ Chứng minh : tam giác AMD tam giác ACMBel Chứng minh ADBCf/ Chứng minh AD // BCg/ Trên DC kéo dài lấy điểm N sao cho CD CN (C ko bằng N) chứng minh : BN // AC.giúp em với ạ:(((((
Đọc tiếp
Cho tam giác ABC. M là trung điểm AC.Trên tia đối của tia MB lấy điểm D sao cho BM=MD.
al Chứng minh : tam giác ABM = tam giác CDM
b/ Chứng minh : AB = CD
b/ Chứng minh : AB // CD
d/ Chứng minh : tam giác AMD =tam giác ACMB
el Chứng minh AD=BC
f/ Chứng minh AD // BC
g/ Trên DC kéo dài lấy điểm N sao cho CD =CN (C ko bằng N) chứng minh : BN // AC.
giúp em với ạ:(((((














