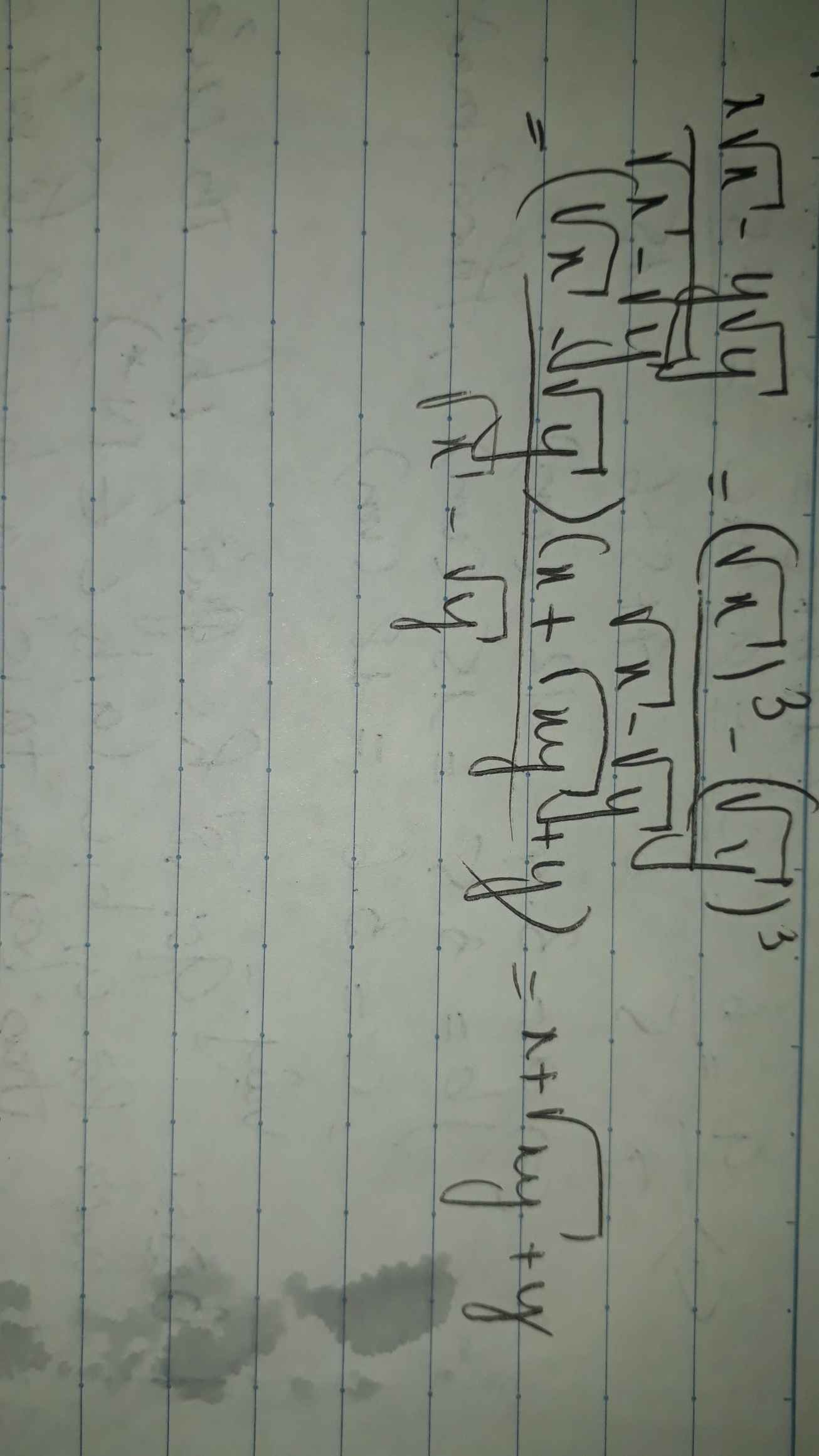Lời giải:

a) ĐK: $x\geq 0; y\geq 0; x\neq y$

\(A=\left[\frac{(\sqrt{x}-\sqrt{y})(\sqrt{x}+\sqrt{y})}{\sqrt{x}-\sqrt{y}}-\frac{(\sqrt{x}-\sqrt{y})(x+\sqrt{xy}+y)}{(\sqrt{x}-\sqrt{y})(\sqrt{x}+\sqrt{y})}\right]:\frac{x-\sqrt{xy}+y}{\sqrt{x}+\sqrt{y}}\)

\(=\left(\sqrt{x}+\sqrt{y}-\frac{x+\sqrt{xy}+y}{\sqrt{x}+\sqrt{y}}\right).\frac{\sqrt{x}+\sqrt{y}}{x-\sqrt{xy}+y}\)

\(=\frac{\sqrt{xy}}{\sqrt{x}+\sqrt{y}}.\frac{\sqrt{x}+\sqrt{y}}{x-\sqrt{xy}+y}=\frac{\sqrt{xy}}{x-\sqrt{xy}+y}\)

b) \(1-A=\frac{(\sqrt{x}-\sqrt{y})^2}{x-\sqrt{xy}+y}>0\) với mọi $x\neq y; x,y\geq 0$

$\Rightarrow A< 1$

\(\dfrac{x\sqrt{x}-y\sqrt{y}}{\sqrt{x}-\sqrt{y}}=x+\sqrt{xy}+y\)

a:

Sửa đề: \(A=\left(\dfrac{\left(\sqrt{x}-\sqrt{y}\right)\left(\sqrt{x}+\sqrt{y}\right)}{\sqrt{x}-\sqrt{y}}+\dfrac{\sqrt{x^3}-\sqrt{y^3}}{y-x}\right)\cdot\dfrac{\sqrt{x}+\sqrt{y}}{x-\sqrt{xy}+y}\)

 \(A=\left(\dfrac{\left(\sqrt{x}-\sqrt{y}\right)\left(\sqrt{x}+\sqrt{y}\right)}{\sqrt{x}-\sqrt{y}}+\dfrac{x\sqrt{x}-y\sqrt{y}}{y-x}\right)\cdot\dfrac{\sqrt{x}+\sqrt{y}}{x-\sqrt{xy}+y}\)

\(A=\left(\sqrt{x}+\sqrt{y}-\dfrac{x+\sqrt{xy}+y}{\sqrt{x}+\sqrt{y}}\right)\cdot\dfrac{\sqrt{x}+\sqrt{y}}{x-\sqrt{xy}+y}\)

\(=\dfrac{x+2\sqrt{xy}+y-x-\sqrt{xy}-y}{\sqrt{x}+\sqrt{y}}\cdot\dfrac{\sqrt{x}+\sqrt{y}}{x-\sqrt{xy}+y}\)

\(=\dfrac{\sqrt{xy}}{x-\sqrt{xy}+y}\)

b: căn xy>0

\(x-\sqrt{xy}+y=x-2\cdot\sqrt{x}\cdot\dfrac{1}{2}\sqrt{y}+\dfrac{1}{4}y+\dfrac{3}{4}y\)

\(=\left(\sqrt{x}-\dfrac{1}{2}\sqrt{y}\right)^2+\dfrac{3}{4}y>0\)

=>A>0

\(A=\dfrac{x\sqrt{x}+y\sqrt{y}}{\sqrt{x}+\sqrt{y}}=x-\sqrt{xy}+y\)

\(B=\dfrac{\sqrt{x}-\sqrt{y}}{x\sqrt{x}-y\sqrt{y}}=\dfrac{1}{x+\sqrt{xy}+y}\)

\(C=\dfrac{3\sqrt{3}+x\sqrt{x}}{3-\sqrt{3x}+x}=\sqrt{x}+\sqrt{3}\)

\(D=\dfrac{x+\sqrt{5x}+5}{x\sqrt{x}-5\sqrt{5}}=\dfrac{1}{\sqrt{x}-\sqrt{5}}\)

\(\dfrac{x\sqrt{y}+y\sqrt{x}}{\sqrt{xy}}:\dfrac{1}{\sqrt{x}-\sqrt{y}}=\dfrac{\sqrt{xy}\left(\sqrt{x}+\sqrt{y}\right)}{\sqrt{xy}}.\left(\sqrt{x}-\sqrt{y}\right)=\left(\sqrt{x}+\sqrt{y}\right)\left(\sqrt{x}-\sqrt{y}\right)=x-y\)

1. ĐKXĐ : \(xy>0\)

Ta có : \(P=\left(\dfrac{\left(\sqrt{x}-\sqrt{y}\right)\left(\sqrt{x}+\sqrt{y}\right)}{\sqrt{x}-\sqrt{y}}+\dfrac{\left(\sqrt{x}-\sqrt{y}\right)\left(x+\sqrt{xy}+y\right)}{-\left(\sqrt{x}-\sqrt{y}\right)\left(\sqrt{x}+\sqrt{y}\right)}\right)\left(\dfrac{\sqrt{x}+\sqrt{y}}{x-2\sqrt{xy}+y+\sqrt{xy}}\right)\)

\(=\dfrac{\left(\sqrt{x}-\sqrt{y}\right)\left(\sqrt{x}+\sqrt{y}\right)\left(\sqrt{x}+\sqrt{y}\right)-\left(\sqrt{x}-\sqrt{y}\right)\left(x+\sqrt{xy}+y\right)}{\left(\sqrt{x}+\sqrt{y}\right)\left(\sqrt{x}-\sqrt{y}\right)}\left(\dfrac{\sqrt{x}+\sqrt{y}}{x-2\sqrt{xy}+y+\sqrt{xy}}\right)\)

\(=\dfrac{\left(\left(\sqrt{x}-\sqrt{y}\right)\left(\sqrt{x}+\sqrt{y}\right)\left(\sqrt{x}+\sqrt{y}\right)-\left(\sqrt{x}-\sqrt{y}\right)\left(x+\sqrt{xy}+y\right)\right)\left(\sqrt{x}+\sqrt{y}\right)}{\left(\sqrt{x}+\sqrt{y}\right)\left(\sqrt{x}-\sqrt{y}\right)\left(x-\sqrt{xy}+y\right)}\)

\(=\dfrac{\left(\sqrt{x}-\sqrt{y}\right)\left(\sqrt{x}+\sqrt{y}\right)\left(\sqrt{x}+\sqrt{y}\right)-\left(\sqrt{x}-\sqrt{y}\right)\left(x+\sqrt{xy}+y\right)}{\left(\sqrt{x}-\sqrt{y}\right)\left(x-\sqrt{xy}+y\right)}\)

\(=\dfrac{\left(\sqrt{x}+\sqrt{y}\right)^2-\left(x+\sqrt{xy}+y\right)}{x-\sqrt{xy}+y}=\dfrac{x+2\sqrt{xy}+y-x-\sqrt{xy}-y}{x-\sqrt{xy}+y}\)

\(=\dfrac{\sqrt{xy}}{x-\sqrt{xy}+y}\)

2. Ta thấy : \(x-\sqrt{xy}+y=x-\dfrac{2.\sqrt{x}.\sqrt{y}}{2}+\dfrac{y}{4}+\dfrac{3y}{4}\)

\(=\left(\sqrt{x}-\dfrac{\sqrt{y}}{2}\right)^2+\dfrac{3y}{4}\)

Mà \(\left\{{}\begin{matrix}\left(\sqrt{x}-\dfrac{\sqrt{y}}{2}\right)^2\ge0\\\dfrac{3y}{4}\ge0\end{matrix}\right.\)

\(\Rightarrow x-\sqrt{xy}+y\ge0\)

Lại có : \(\sqrt{xy}\ge0\)

\(\Rightarrow P\ge0\) ( ĐPCM )

Lời giải:

\(A=\frac{x+y}{\sqrt{xy}}: \frac{x-y}{\sqrt{xy}}=\frac{x+y}{\sqrt{xy}}.\frac{\sqrt{xy}}{x-y}=\frac{x+y}{x-y}\)

\(=\frac{1+a+1-a}{1+a-(1-a)}=\frac{2}{2a}=\frac{1}{a}\)

a) \(B=\left(\dfrac{x-y}{\sqrt{x}-\sqrt{y}}+\dfrac{x\sqrt{x}-y\sqrt{y}}{y-x}\right):\dfrac{\left(\sqrt{x}-\sqrt{y}\right)^2+\sqrt{xy}}{\sqrt{x}+\sqrt{y}}\left(x,y\ge0;x\ne y\right)\)

\(B=\left[\dfrac{\left(\sqrt{x}-\sqrt{y}\right)\left(\sqrt{x}+\sqrt{y}\right)}{\sqrt{x}-\sqrt{y}}-\dfrac{\left(\sqrt{x}\right)^3-\left(\sqrt{y}\right)^3}{x-y}\right]:\dfrac{x-2\sqrt{xy}+y+\sqrt{xy}}{\sqrt{x}+\sqrt{y}}\)

\(B=\left[\left(\sqrt{x}+\sqrt{y}\right)-\dfrac{\left(\sqrt{x}-\sqrt{y}\right)\left(x+\sqrt{xy}+y\right)}{\left(\sqrt{x}-\sqrt{y}\right)\left(\sqrt{x}+\sqrt{y}\right)}\right]:\dfrac{x+\sqrt{xy}+y}{\sqrt{x}+\sqrt{y}}\)

\(B=\left[\left(\sqrt{x}+\sqrt{y}\right)-\dfrac{x+\sqrt{xy}+y}{\sqrt{x}+\sqrt{y}}\right]:\dfrac{x+\sqrt{xy}+y}{\sqrt{x}+\sqrt{y}}\)

\(B=\dfrac{\left(\sqrt{x}+\sqrt{y}\right)^2-x-\sqrt{xy}-y}{\sqrt{x}+\sqrt{y}}\cdot\dfrac{\sqrt{x}+\sqrt{y}}{x+\sqrt{xy}+y}\)

\(B=\dfrac{x+2\sqrt{xy}+y-x-\sqrt{xy}-y}{\sqrt{x}+\sqrt{y}}\cdot\dfrac{\sqrt{x}+\sqrt{y}}{x+\sqrt{xy}+y}\)

\(B=\dfrac{\sqrt{xy}}{\sqrt{x}+\sqrt{y}}\cdot\dfrac{\sqrt{x}+\sqrt{y}}{x+\sqrt{xy}+y}\)

\(B=\dfrac{\sqrt{xy}}{x+\sqrt{xy}+y}\)

b) Xét tử: 

\(\sqrt{xy}\ge0\forall x,y\) (xác định) (1) 

Xét mẫu: 

\(x+\sqrt{xy}+y\)

\(=\left(\sqrt{x}\right)^2+2\cdot\dfrac{1}{2}\sqrt{y}\cdot\sqrt{x}+\left(\dfrac{1}{2}\sqrt{y}\right)^2+\dfrac{3}{4}y\)

\(=\left(\sqrt{x}+\dfrac{1}{2}\sqrt{y}\right)^2+\dfrac{3}{4}y\)

Mà: \(\left(\sqrt{x}+\dfrac{1}{2}\sqrt{y}\right)^2\ge0\forall x,y\) (xác định), còn: \(\dfrac{3}{4}y\ge0\) vì theo đkxđ thì \(y\ge0\) (2) 

Từ (1) và (2) ⇒ B luôn không âm với mọi x,y (\(B\ge0\)) (đpcm)