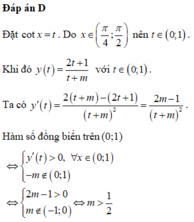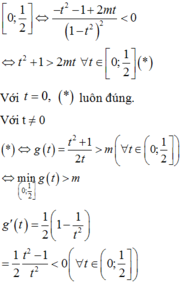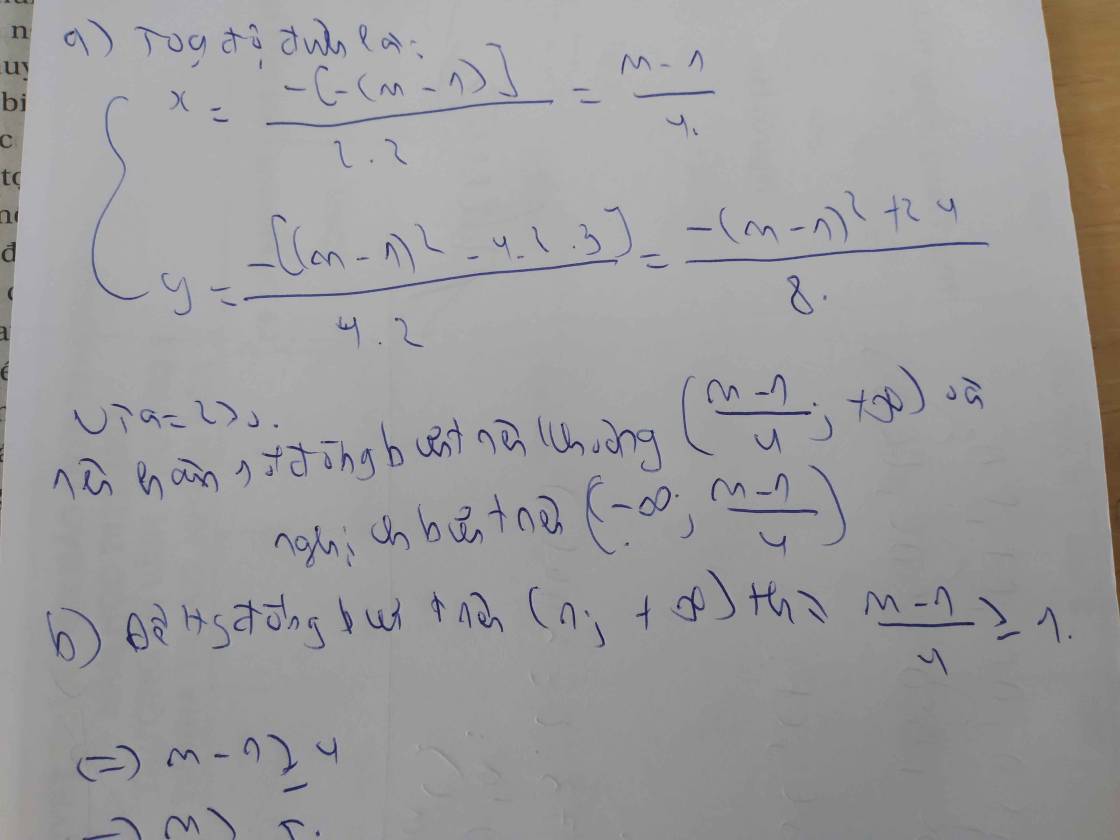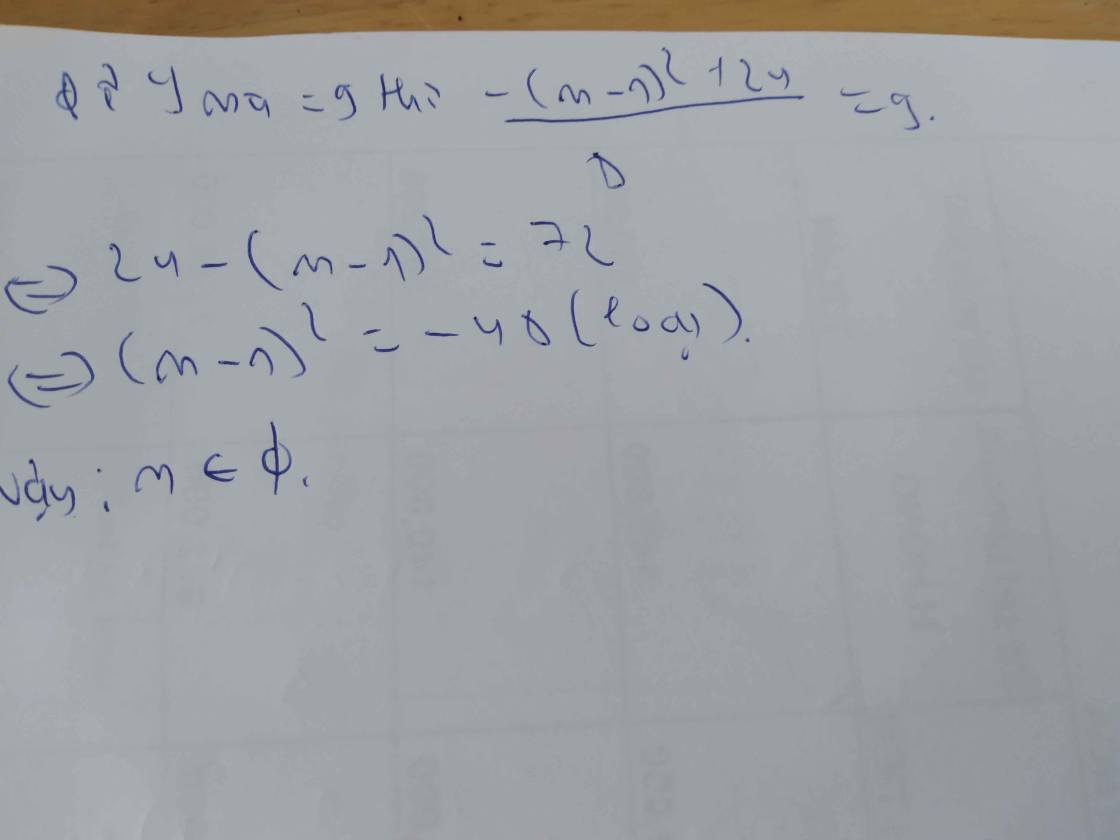Giá trị của m để hàm số y = cot x /cot x − m nghịch biến trên (π/4; π/2).
Những câu hỏi liên quan
Giá trị m để hàm số y
c
o
t
x
-
2
c
o
t
x
-
m
nghịch biến trên
π
4
;
π
2
là A. m
≤...
Đọc tiếp
Giá trị m để hàm số y = c o t x - 2 c o t x - m nghịch biến trên π 4 ; π 2 là
A. m ≤ 0 hoặc 1 ≤ m < 2
B. 1 ≤ m < 2
C. m ≤ 0
D. m > 2
Chọn A.
Đặt t = cot x,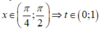 
Ta có: 
Để hàm số
c
o
t
x
-
2
c
o
t
x
-
m
nghịch biến trên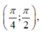 
thì hàm số 
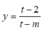đồng biến trên (0;1)
Xét hàm số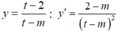 
Để hàm số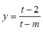 
đồng biến trên (0;1) thì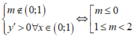 
Đúng 0
Bình luận (0)
Cho hàm số f(x)3 sinx+2. Gọi S là tập hợp các giá trị nguyên của tham số m để hàm số
y
f
3
(
x
)
-
3
mf
2
(
x
)
+
3
(
m...
Đọc tiếp
Cho hàm số f(x)=3 sinx+2. Gọi S là tập hợp các giá trị nguyên của tham số m để hàm số y = f 3 ( x ) - 3 mf 2 ( x ) + 3 ( m 2 - 4 ) f ( x ) - m nghịch biến trên khoảng (0;π/2). Số tập con của S bằng
A. 1
B. 2.
C. 4.
D. 16.
Tìm các giá trị thực của m để hàm số
y
sin
x
-
3
sin
x
-
m
nghịch biến trên
π
2
;
π
Đọc tiếp
Tìm các giá trị thực của m để hàm số y = sin x - 3 sin x - m nghịch biến trên π 2 ; π
Tìm tất cả các giá trị thực của tham số m để hàm số
y
cosx
+
m
cosx
−
m
nghịch biến trên
π
2
,
π
.
A.
−
1
m
0
B.
m...
Đọc tiếp
Tìm tất cả các giá trị thực của tham số m để hàm số y = cosx + m cosx − m nghịch biến trên π 2 , π .
A. − 1 < m < 0
B. m ≥ 0
C. m ≤ − 1
D. − 1 ≤ m ≤ 0
Tìm tất cả các giá trị thực của tham số m để hàm số
y
cos
x
+
m
c
o
s
x
-
m
nghịch biến trên
π
2
;
π
A.
m
≤
-
1...
Đọc tiếp
Tìm tất cả các giá trị thực của tham số m để hàm số y = cos x + m c o s x - m nghịch biến trên π 2 ; π
A. m ≤ - 1
B. -1 < m < 0
C. - 1 ≤ m ≤ 0
D. m ≥ 0
Đáp án A
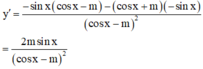
Để hàm số nghịch biến trên π 2 ; π ta cần có
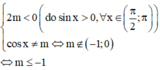
Đúng 0
Bình luận (0)
Tìm m để hàm số
y
2
c
o
t
x
+
1
c
o
t
x
+
m
đồng biến trên
π
4
;
π
2
? A.
m...
Đọc tiếp
Tìm m để hàm số y = 2 c o t x + 1 c o t x + m đồng biến trên π 4 ; π 2 ?
A. m ∈ ( - ∞ ; - 2 )
B. m ∈ ( - ∞ ; - 1 ] ∪ [ 0 ; 1 2 )
C. m ∈ ( 2 ; + ∞ )
D. m ∈ ( 1 2 ; + ∞ )
Tìm tất cả giá trị thực của tham số m sao cho hàm số
y
f
(
x
)
m
-
2
sin
x
1
+
cos
2...
Đọc tiếp
Tìm tất cả giá trị thực của tham số m sao cho hàm số y = f ( x ) = m - 2 sin x 1 + cos 2 x nghịch biến trên khoảng (0; π / 6 )
A.
.
B.
.
C.
.
D.
.
Chọn D
Cách1:
Ta có: 
.
Vậy 
.
Đặt 
.
Vậy 
.
Ta có: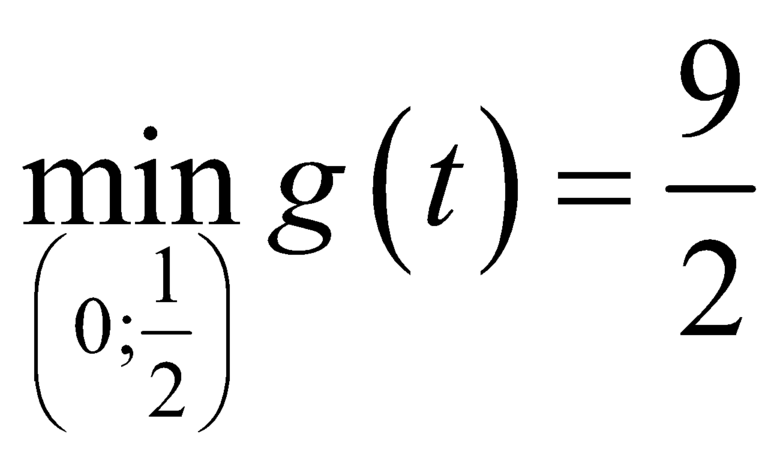
. Vậy 
.
Đúng 0
Bình luận (0)
29 tháng 7 2021 lúc 21:11
3. Có bao nhiêu giá trị nguyên của tham số m để hàm số \(y=\dfrac{x+1}{x+3m}\) nghịch biến trên khoảng(6;+\(\infty\) )?
4. Có bao nhiêu giá trị nguyên của tham số m để hàm số \(y=\dfrac{x+2}{x+3m}\) đồng biến trên khoảng (-\(\infty\);-6)?
3.
\(y'=\dfrac{3m-1}{\left(x+3m\right)^2}\)
Hàm nghịch biến trên khoảng đã cho khi:
\(\left\{{}\begin{matrix}3m-1< 0\\-3m\le6\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}m< \dfrac{1}{3}\\m\ge-2\end{matrix}\right.\)
\(\Rightarrow-2\le m< \dfrac{1}{3}\Rightarrow m=\left\{-2;-1;0\right\}\)
4.
\(y'=\dfrac{3m-2}{\left(x+3m\right)^2}\)
Hàm đồng biến trên khoảng đã cho khi:
\(\left\{{}\begin{matrix}3m-2>0\\-3m\ge-6\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}m>\dfrac{2}{3}\\m\le2\end{matrix}\right.\)
\(\Rightarrow\dfrac{2}{3}< m\le2\Rightarrow m=\left\{1;2\right\}\)
Đúng 1
Bình luận (0)
Có bao nhiêu giá trị nguyên dương của tham số m để hàm số
y
m
-
sin
x
cos
2
x
nghịch biến trên khoảng [0;π/6]? A. 1. B. 0. C. 2. D. Vô số.
Đọc tiếp
Có bao nhiêu giá trị nguyên dương của tham số m để hàm số y = m - sin x cos 2 x nghịch biến trên khoảng [0;π/6]?
A. 1.
B. 0.
C. 2.
D. Vô số.
cho hàm số y = 2x2 - (m - 1 )x +3, m là tham số
a. tìm khoảng đồng biến, nghịch biến của hàm số
b/ tìm các giái trị của m để hàm số đồng biến trên khoảng 1;+∞
c. tìm m để hàm số nghịch biến trên khoàng -4;8
d. tìm m để giá trị nhỏ nhất của hàm số là 9
