Đáp án A
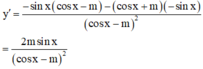
Để hàm số nghịch biến trên π 2 ; π ta cần có
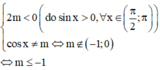
Đáp án A
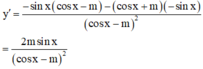
Để hàm số nghịch biến trên π 2 ; π ta cần có
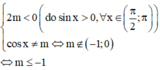
Tìm tất cả các giá trị thực của tham số m để hàm số y = cosx + m cosx − m nghịch biến trên π 2 , π .
A. − 1 < m < 0
B. m ≥ 0
C. m ≤ − 1
D. − 1 ≤ m ≤ 0
Tìm tập hợp tất cả các giá trị thực của tham số m để hàm số y = m cos x + 1 cos x + m đồng biến trên khoảng 0 ; π 3
A. - 1 ; 1
B. - ∞ ; - 1 ∪ 1 ; + ∞
C. [ - 1 ; - 1 2 )
D. - 1 ; - 1 2
Cho hàm số f(x)=3 sinx+2. Gọi S là tập hợp các giá trị nguyên của tham số m để hàm số y = f 3 ( x ) - 3 mf 2 ( x ) + 3 ( m 2 - 4 ) f ( x ) - m nghịch biến trên khoảng (0;π/2). Số tập con của S bằng
A. 1
B. 2.
C. 4.
D. 16.
Tìm tất cả các giá trị thực của tham số m để hàm số y = cos x − 2 cos x − m nghịch biến trên khoảng 0 ; π 2
A. m > 2
B. m ≤ 0 hoặc 1 ≤ m < 2
C. m ≤ 2
D. m ≤ 0
Có bao nhiêu giá trị nguyên dương của tham số m để hàm số y = m - sin x cos 2 x nghịch biến trên khoảng [0;π/6]?
A. 1.
B. 0.
C. 2.
D. Vô số.
Tập hợp tất cả các giá trị thực của tham số m để hàm số y = − 1 3 x 3 + x 2 − m x + 1 nghịch biến trên khoảng 0 ; + ∞ là:
A. m ∈ 1 ; + ∞
B. m ∈ 0 ; + ∞
C. m ∈ 0 ; + ∞
D. m ∈ 1 ; + ∞
Tìm tất cả các giá trị thực của tham số m sao cho hàm số y = m x + 2 m + 1 x - m nghịch biến trên khoảng 0 ; + ∞
A. m ∈ 0 ; + ∞
B. m ∈ ( - ∞ ; 0 ] \ - 1
C. m ∈ R \ - 1
D. m ∈ R
Tìm tất cả các giá trị thực của tham số m sao cho hàm số y = mx + 2 m + 1 x − m nghịch biến trên khoảng 0 ; + ∞ .
A. m ∈ ℝ \ − 1
B. m ∈ − ∞ ; 0 \ − 1
C. m ∈ 0 ; + ∞
D. m ∈ ℝ
Tìm tất cả các giá trị của tham số m để hàm số y = 2 cos s x + 3 2 c o s x - m nghịch biến trên khoảng 0 ; π 3
![]()
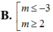
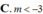
![]()