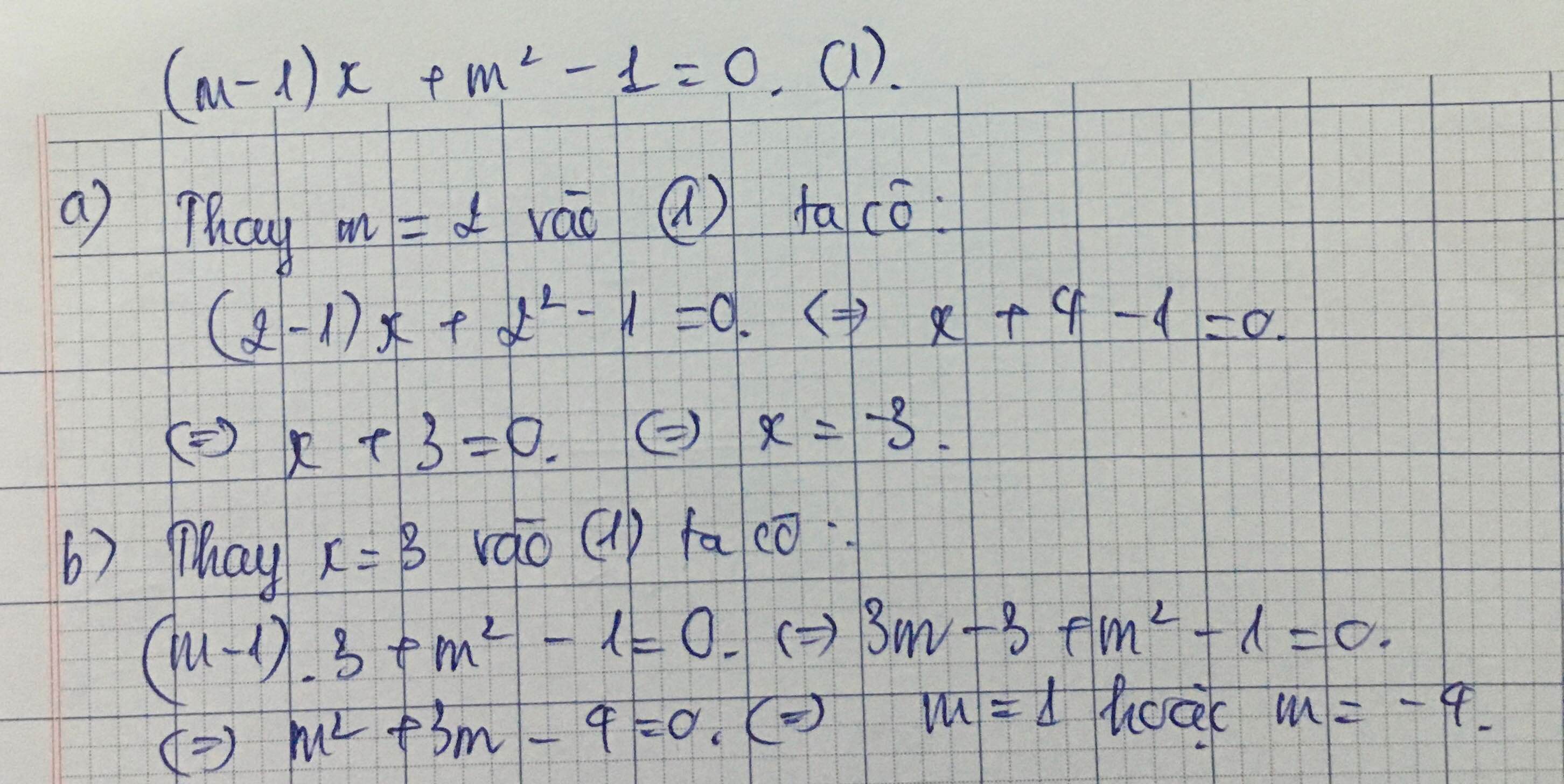a) Thay m=2 vào phương trình \(x^2+2\left(m-1\right)x-4m=0\), ta được:

\(x^2+2\cdot\left(2-1\right)x-4\cdot2=0\)

\(\Leftrightarrow x^2+2x-8=0\)(1)

\(\Delta=b^2-4ac=2^2-4\cdot1\cdot\left(-8\right)=4+32=36\)

Vì \(\Delta>0\) nên phương trình (1) có hai nghiệm phân biệt là:

\(\left\{{}\begin{matrix}x_1=\dfrac{-b-\sqrt{\Delta}}{2a}\\x_2=\dfrac{-b+\sqrt{\Delta}}{2a}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x_1=\dfrac{-2-\sqrt{36}}{2\cdot1}=\dfrac{-2-6}{2}=-4\\x_2=\dfrac{-2+\sqrt{36}}{2\cdot1}=\dfrac{-2+6}{2}=2\end{matrix}\right.\)

Vậy: Khi m=2 thì phương trình \(x^2+2\left(m-1\right)x-4m=0\) có hai nghiệm phân biệt là \(x_1=-4;x_2=2\)

b) Ta có: \(x^2+2\left(m-1\right)x-4m=0\)

\(\Delta=\left[2\left(m-1\right)\right]^2-4\cdot1\cdot\left(-4\right)\)

\(\Leftrightarrow\Delta=\left(2m-2\right)^2+16>0\forall m\)

\(\forall m\) thì phương trình \(x^2+2\left(m-1\right)x-4m=0\) luôn có hai nghiệm phân biệt là: 

\(\left\{{}\begin{matrix}x_1=\dfrac{-\left(2m-2\right)-\sqrt{\Delta}}{2}\\x_2=\dfrac{-\left(2m-2\right)+\sqrt{\Delta}}{2}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x_1=\dfrac{-2m+2-\sqrt{\left(2m-2\right)^2+16}}{2}\\x_2=\dfrac{-2m+2+\sqrt{\left(2m-2\right)^2+16}}{2}\end{matrix}\right.\)

Để x₁ và x₂ là hai số đối nhau thì \(x_1+x_2=0\)

\(\Leftrightarrow\dfrac{-2m+2-\sqrt{\left(2m-2\right)^2+16}}{2}+\dfrac{-2m+2+\sqrt{\left(2m-2\right)^2+16}}{2}=0\)

\(\Leftrightarrow-2m+2-2m+2=0\)

\(\Leftrightarrow-4m+4=0\)

\(\Leftrightarrow-4m=-4\)

hay m=1

Vậy: Khi m=1 thì phương trình \(x^2+2\left(m-1\right)x-4m=0\) có hai nghiệm phân biệt x₁ và x₂ thỏa mãn x₁ và x₂ là hai số đối nhau

a, Với m = 2 (1)<=>x^2+2x-8=0 rồi tính ra thôi

b, Để PT có 2 nghiệm PB thì 

a, Đặt \(x^2=t\left(t\ge0\right)\)

Khi đó \(PT< =>t^1+4t-5=0\)

\(< =>t^2-1+4t-4=0\)

\(< =>\left(t-1\right)\left(t+1\right)+4\left(t-1\right)=0\)

\(< =>\left(t-1\right)\left(t+5\right)=0\)

\(< =>\orbr{\begin{cases}t=1\left(tm\right)\\t=-5\left(loai\right)\end{cases}}\)

\(< =>x^2=1< =>\orbr{\begin{cases}x=-1\\x=1\end{cases}}\)

Vậy ...

Thay m = 2 vào , ta có :

\(PT< =>x^2-2\left(2+1\right)x+2^2+3.2-4=0\)

\(< =>x^2-6x+6=0\)

\(< =>\left(x^2-6x+9\right)-\sqrt{3}^2=0\)

\(< =>\left(x-3-\sqrt{3}\right)\left(x-3+\sqrt{3}\right)=0\)

\(< =>\orbr{\begin{cases}x=3+\sqrt{3}\\x=3-\sqrt{3}\end{cases}}\)

x=1

Ai kb vs mink ko mink k cho

x(x-1)+(1-x)=0\(\Leftrightarrow x^2-x+1-x=0\Leftrightarrow x^2-2x+1=0\Leftrightarrow\left(x-1\right)^2=0\Leftrightarrow x=1\)

Vậy phương trình có 1 nghiệm duy nhất là x=1

\(x\left(x-1\right)+\left(1-x\right)=0\)

\(x\left(x-1\right)-\left(x-1\right)=0\)

\(\Rightarrow\left(x-1\right)\left(x-1\right)=0\)

\(\Rightarrow\left(x-1\right)^2=0\)

\(\Rightarrow x-1=0\)

\(\Rightarrow x=1\)

(x - 1) + 2(1 - x) = 0

<=> x - 1 + 2 - 2x = 0

<=> -x + 1 = 0

<=> - x = -1

<=> x = 1

\(\left(x-1\right)+2\left(1-x\right)=0\)

           \(x-1+2-2x=0\)

                          \(-x+1=0\)

                                       \(x=-1\)

Vậy \(x=-1\)

Vậy phương trình có tập nghiệm S = {1}

1; Khi m=1 thì pt sẽ là \(\sqrt{x+1}=x+1\)

=>(x+1)^2=(x+1)

=>x(x+1)=0

=>x=0hoặc x=-1

2: \(\Leftrightarrow x+1=\left(x+m\right)^2\)

=>x^2+2mx+m^2-x-1=0

=>x^2+x(2m-1)+m^2-1=0

Δ=(2m-1)^2-4(m^2-1)

=4m^2-4m+1-4m^2+4

=-4m+5

Để pt có 2 nghiệm pb thì -4m+5>0

=>-4m>-5

=>m<5/4

Để pt có nghiệm kép thì 5-4m=0

=>m=5/4

Để pt vô nghiệm thì -4m+5<0

=>m>5/4

\(\left(x+1\right)\left(x+3\right)\left(x+5\right)\left(x+7\right)+15=\left[\left(x+1\right)\left(x+7\right)\right]\left[\left(x+3\right)\left(x+5\right)\right]+15=\left(x^2+8x+7\right)\left(x^2+8x+15\right)+15=0\)\(Dat:x^2+8x+7=a\Rightarrow a\left(a+8\right)+15=0\Leftrightarrow a^2+8a+15=0\Leftrightarrow\left(a+3\right)\left(a+5\right)=0\Leftrightarrow\left[{}\begin{matrix}a=-3\\a=-5\end{matrix}\right.\)\(+,a=-5\Rightarrow x^2+8x+7=-5\Leftrightarrow x^2+8x+16=4\Leftrightarrow\left(x+4\right)^2=4\Rightarrow\left[{}\begin{matrix}x+4=-2\\x+4=2\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=-6\left(thoaman\right)\\x=2\left(loai\right)\end{matrix}\right.\)\(+,a=-3\Rightarrow x^2+8x+7=-3\Leftrightarrow x^2+8x+16=6\Leftrightarrow\left(x+4\right)^2=6\Leftrightarrow\left[{}\begin{matrix}x+4=-\sqrt{6}\\x+4=\sqrt{6}\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=-\left(\sqrt{6}+4\right)\left(thoaman\right)\\x=\sqrt{6}-4\left(thoaman\right)\end{matrix}\right.\) \(\Rightarrow x\in\left\{\sqrt{6}-4;-\sqrt{6}-4;-6\right\}\)

\(x^2-3x+2+\left|x-1\right|=0\)

\(\Leftrightarrow x^2-2x-x+2+\left|x-1\right|=0\)

\(\Leftrightarrow x\left(x-2\right)-\left(x-2\right)+\left|x-1\right|=0\)

\(\Leftrightarrow\left(x-2\right)\left(x-1\right)+\left|x-1\right|=0\)

\(\Leftrightarrow\left|x-1\right|=\left(x-1\right)\left(2-x\right)\)

\(\Leftrightarrow\left[{}\begin{matrix}x-1=\left(x-1\right)\left(2-x\right)\left(x\ge1\right)\\x-1=\left(x-1\right)\left(x-2\right)\left(x< 1\right)\end{matrix}\right.\)

\(\Leftrightarrow\left[{}\begin{matrix}\left(x-1\right)\left(2-x-1\right)=0\\\left(x-1\right)\left(x-2-1\right)=0\end{matrix}\right.\)

\(\Leftrightarrow\left[{}\begin{matrix}x=1\\\left[{}\begin{matrix}x=1\left(loai\right)\\x=3\left(loai\right)\end{matrix}\right.\end{matrix}\right.\)