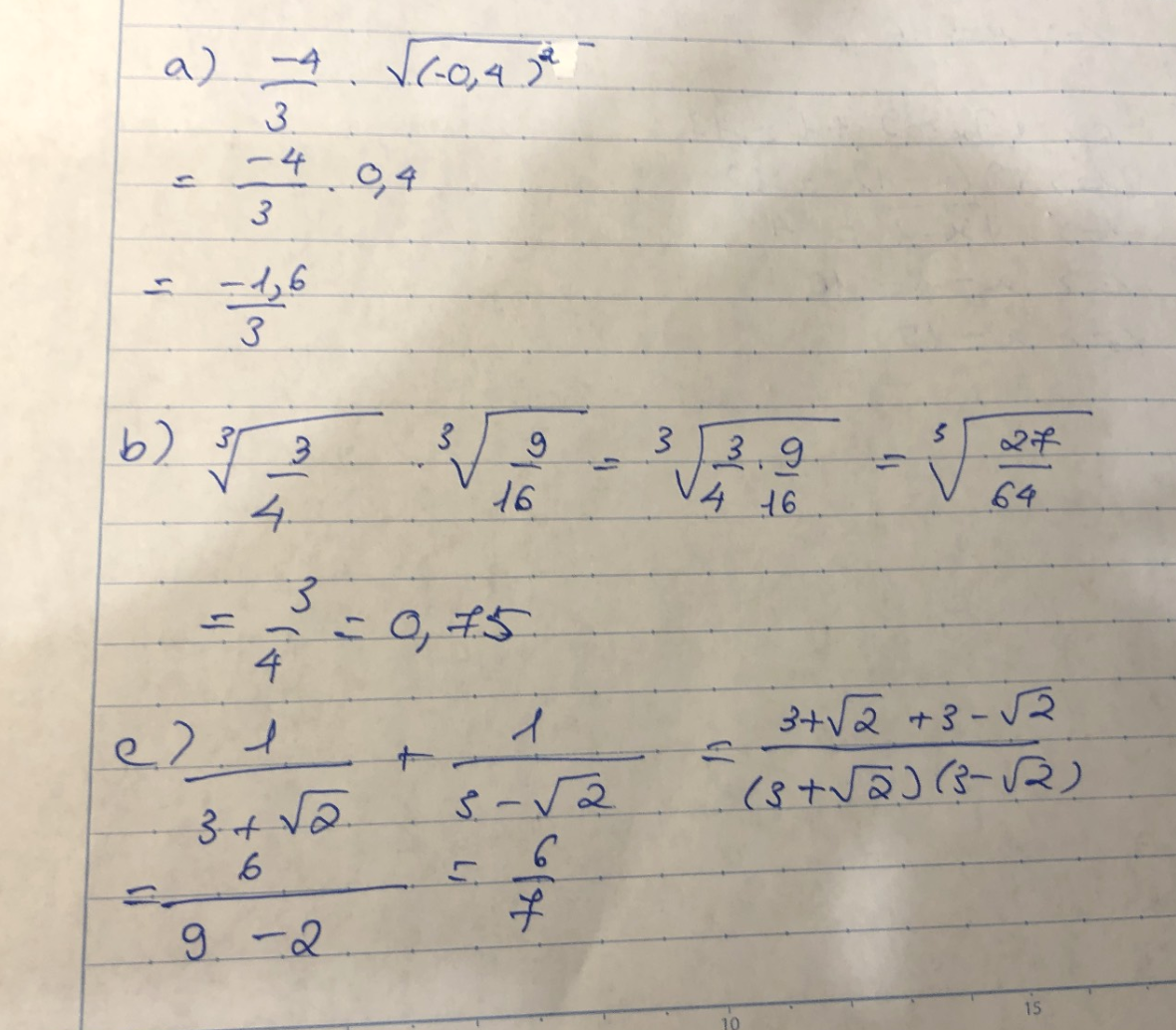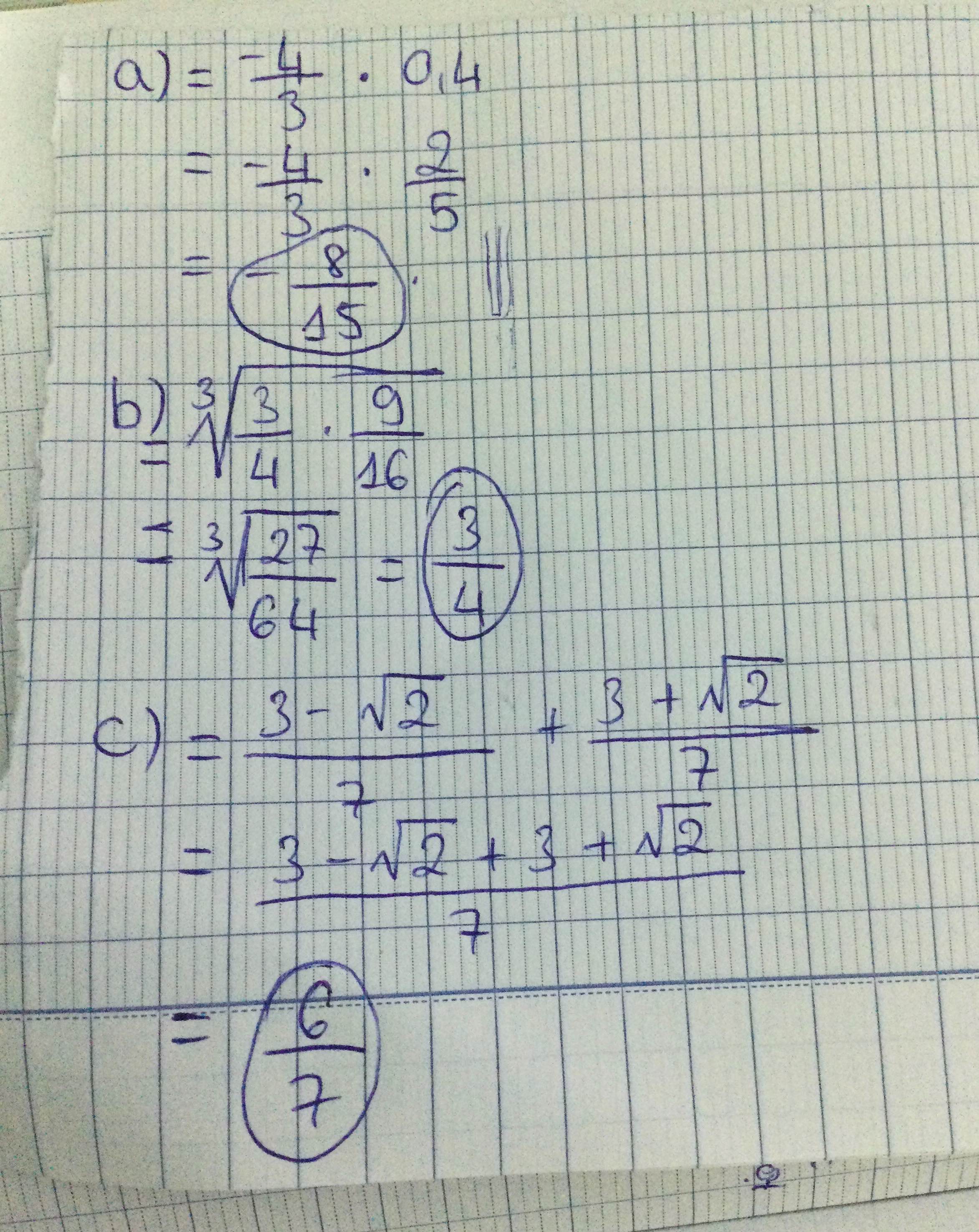\(e,\sqrt{\dfrac{9}{169}}=\dfrac{\sqrt{9}}{\sqrt{169}}=\dfrac{\sqrt{3^2}}{\sqrt{13^2}}=\dfrac{3}{13}\)

\(f,\sqrt{1\dfrac{9}{16}}=\sqrt{\dfrac{25}{16}}=\dfrac{\sqrt{25}}{\sqrt{16}}=\dfrac{\sqrt{5^2}}{\sqrt{4^2}}=\dfrac{5}{4}\)

\(g,\dfrac{\sqrt{2300}}{\sqrt{23}}=\sqrt{\dfrac{2300}{23}}=\sqrt{100}=\sqrt{10^2}=10\)

\(h,\dfrac{\sqrt{12,5}}{\sqrt{0,5}}=\sqrt{\dfrac{12,5}{0,5}}=\sqrt{25}=\sqrt{5^2}=5\)

e, \(\sqrt{\dfrac{9}{169}}\)

\(=\sqrt{\dfrac{3^2}{13^2}}\)

\(=\dfrac{3}{13}\)

f, \(\sqrt{1\dfrac{9}{16}}\)

\(=\sqrt{\dfrac{25}{16}}\)

\(=\sqrt{\dfrac{5^2}{4^2}}\)

\(=\dfrac{5}{4}\)

g, \(\dfrac{\sqrt{2300}}{\sqrt{23}}\)

\(=\dfrac{10\sqrt{23}}{\sqrt{23}}\)

\(=10\)

h, \(\dfrac{\sqrt{12,5}}{\sqrt{0,5}}\)

\(=\dfrac{\dfrac{5\sqrt{2}}{2}}{\dfrac{\sqrt{2}}{2}}\)

\(=\dfrac{\dfrac{5\sqrt{2}}{2}\cdot2}{\sqrt{2}}\)

\(=\dfrac{5\sqrt{2}}{\sqrt{2}}=5\)

\(=\left(\dfrac{3}{2}-3\right).\sqrt{\dfrac{25}{16}}=\left(-\dfrac{3}{2}\right).\dfrac{5}{4}=-\dfrac{15}{8}\)

\(a) \sqrt{4x^2− 9} = 2\sqrt{x + 3}\)

\(ĐK:x\ge\dfrac{3}{2}\)

\(pt\Leftrightarrow4x^2-9=4\left(x+3\right)\)

\(\Leftrightarrow4x^2-9=4x+12\)

\(\Leftrightarrow4x^2-4x-21=0\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{1-\sqrt{22}}{2}\left(l\right)\\x=\dfrac{1+\sqrt{22}}{2}\left(tm\right)\end{matrix}\right.\)

\(b)\sqrt{4x-20}+3.\sqrt{\dfrac{x-5}{9}}-\dfrac{1}{3}\sqrt{9x-45}=4\)

\(ĐK:x\ge5\)

\(pt\Leftrightarrow2\sqrt{x-5}+\sqrt{x-5}-\sqrt{x-5}=4\)

\(\Leftrightarrow2\sqrt{x-5}=4\Leftrightarrow\sqrt{x-5}=2\)

\(\Leftrightarrow x-5=4\Leftrightarrow x=9\left(tm\right)\)

\(c)\dfrac{2}{3}\sqrt{9x-9}-\dfrac{1}{4}\sqrt{16x-16}+27.\sqrt{\dfrac{x-1}{81}}=4\)

ĐK:x>=1

\(pt\Leftrightarrow2\sqrt{x-1}-\sqrt{x-1}+3\sqrt{x-1}=4\)

\(\Leftrightarrow4\sqrt{x-1}=4\Leftrightarrow\sqrt{x-1}=1\)

\(\Leftrightarrow x-1=1\Leftrightarrow x=2\left(tm\right)\)

\(d)5\sqrt{\dfrac{9x-27}{25}}-7\sqrt{\dfrac{4x-12}{9}}-7\sqrt{x^2-9}+18\sqrt{\dfrac{9x^2-81}{81}}=0\)

\(ĐK:x\ge3\)

\(pt\Leftrightarrow3\sqrt{x-3}-\dfrac{14}{3}\sqrt{x-3}-7\sqrt{x^2-9}+6\sqrt{x^2-9}=0\)

\(\Leftrightarrow-\dfrac{5}{3}\sqrt{x-3}-\sqrt{x^2-9}=0\Leftrightarrow\dfrac{5}{3}\sqrt{x-3}+\sqrt{x^2-9}=0\)

\(\Leftrightarrow(\dfrac{5}{3}+\sqrt{x+3})\sqrt{x-3}=0\)

\(\Leftrightarrow\sqrt{x-3}=0\)    (vì \(\dfrac{5}{3}+\sqrt{x+3}>0\))

\(\Leftrightarrow x-3=0\Leftrightarrow x=3\left(nhận\right)\)

\(\dfrac{2}{3}\sqrt{9u-9}-\dfrac{1}{4}\sqrt{16u-16}+27\sqrt{\dfrac{u-1}{81}}=4\left(dk:u\ge1\right)\)

\(\Leftrightarrow\dfrac{2}{3}\sqrt{9\left(u-1\right)}-\dfrac{1}{4}\sqrt{16\left(u-1\right)}+27\dfrac{\sqrt{u-1}}{\sqrt{81}}=4\)

\(\Leftrightarrow2\sqrt{u-1}-\sqrt{u-1}+3\sqrt{u-1}=4\\ \Leftrightarrow\sqrt{u-1}.\left(2-1+3\right)=4\\ \Leftrightarrow4\sqrt{u-1}=4\\ \Leftrightarrow\sqrt{u-1}=1\\ \Leftrightarrow u-1=1\\ \Leftrightarrow u=2\left(tm\right)\)

Vậy \(S=\left\{2\right\}\)

a,\(\left(\sqrt{1\dfrac{9}{16}}-\sqrt{\dfrac{9}{16}}\right):5=\left(\sqrt{\dfrac{25}{16}}-\dfrac{3}{4}\right):5=\left(\dfrac{5}{4}-\dfrac{3}{4}\right):5\)

\(=\dfrac{1}{2}:5=\dfrac{1}{10}\)

b,\(\left(\sqrt{3}-2\right)^2\left(\sqrt{3}+2\right)^2=\left[\left(\sqrt{3}-2\right)\left(\sqrt{3}+2\right)\right]^2\)

\(=\left[3-4\right]^2=1\)

c,\(\left(11-4\sqrt{3}\right)\left(11+4\sqrt{3}\right)=11^2-\left(4\sqrt{3}\right)^2\)

\(=121-48=73\)

d,\(\left(\sqrt{2}-1\right)^2-\dfrac{3}{2}\sqrt{\left(-2\right)^2}+\dfrac{4\sqrt{2}}{5}+\sqrt{1\dfrac{11}{25}}.\sqrt{2}\)

\(=2-2\sqrt{2}+1-3+\dfrac{4\sqrt{2}}{5}+\sqrt{\dfrac{36}{25}.2}\)

\(=-2\sqrt{2}+\dfrac{4\sqrt{2}+6\sqrt{2}}{5}\)

\(=-2\sqrt{2}+\dfrac{10\sqrt{2}}{5}=-2\sqrt{2}+2\sqrt{2}=0\)

e,\(\left(1+\sqrt{2021}\right)\sqrt{2022-2\sqrt{2021}}\)

\(=\left(1+\sqrt{2021}\right)\sqrt{2021-2\sqrt{2021}.1+1}\)

\(=\left(1+\sqrt{2021}\right)\sqrt{\left(\sqrt{2021}-1\right)^2}\)

\(=\left(1+\sqrt{2021}\right)\left(\sqrt{2021}-1\right)\)

\(=\sqrt{2021}-1+\sqrt{2021^2}-\sqrt{2021}=2020\)

\(\dfrac{2}{3}\sqrt{27}-\dfrac{9}{2}\sqrt{\dfrac{16}{81}}+\sqrt{\left(1-\sqrt{3}\right)^2}\)

\(=\dfrac{2}{3}\sqrt{3}-\dfrac{9}{2}.\dfrac{4}{9}+\left(1-\sqrt{3}\right)\)

\(=\dfrac{2\sqrt{3}}{3}-2+1-\sqrt{3}\)

\(=-\dfrac{\sqrt{3}}{3}-1\)

\(=-\dfrac{3+\sqrt{3}}{3}\)

a) Ta có: \(\dfrac{-4}{3}\cdot\sqrt{\left(-0.4\right)^2}\)

\(=-\dfrac{4}{3}\cdot0.4\)

\(=\dfrac{-1.6}{3}=-\dfrac{8}{15}\)

b) Ta có: \(\sqrt[3]{\dfrac{3}{4}}\cdot\sqrt[3]{\dfrac{9}{16}}\)

\(=\sqrt[3]{\dfrac{27}{64}}=\dfrac{3}{4}\)

c) Ta có: \(\dfrac{1}{3+\sqrt{2}}+\dfrac{1}{3-\sqrt{2}}\)

\(=\dfrac{3-\sqrt{2}+3+\sqrt{2}}{7}\)

\(=\dfrac{6}{7}\)

a: \(\dfrac{-4}{3}\cdot\sqrt{\left(-0.4\right)^2}=\dfrac{-4}{3}\cdot\dfrac{2}{5}=\dfrac{-8}{15}\)

b: \(\sqrt[3]{\dfrac{3}{4}}\cdot\sqrt[3]{\dfrac{9}{16}}=\dfrac{3}{4}\)