Tìm cặp số (x,y)(x,y) để P=5(2x2−2xy+y2)+2(y−3x+2)P=5(2x2−2xy+y2)+2(y−3x+2) đạt giá trị nhỏ nhất
Những câu hỏi liên quan
a) 3x(x+1)-x(3x+2)
b) 2x(x2-5x+6)+(x-1)(x+3)
c) (x2-xy+y2)-(x2+2xy+y2)
d) (2/5xy+x-y)-(3x+4y)-2/5xy
e) 2xy(x2-4xy+4y2)
f) (x+y)(xy+5)
g) (x3-2x2-x+2):(x-1)
h) (2x2+3x-2):(2x-1)
Cho số phức
z
x
+
y
i
(
x
,
y
∈
R
)
thỏa mãn
z
-
2
+
i
z
+
2
+
5
i
và biểu thức
H
x...
Đọc tiếp
Cho số phức z = x + y i ( x , y ∈ R ) thỏa mãn z - 2 + i = z + 2 + 5 i và biểu thức H = x 2 + y 2 - 3 y + 1 x 2 + y 2 + 2 x - 2 y + 2 x 2 + y 2 - 2 x - 4 y + 5 đạt giá trị nhỏ nhất. Giá trị của 2x + y bằng
A. -6
B. - 6 + 5
C. - 3 - 5
D. - 6 - 5
Tính GTNN, GTLN của các biểu thức sau:
a)A(x,y)=4x2+y2+4x-y+1
b)B(x,y)=2x2+y2+2xy-x+5
Toán lớp 8Lớn nhất - nhỏ nhất
Xem chi tiết
Tìm giá trị lớn nhất A=x(4-x)
Rút gọn rồi tính
A=(7x+5)2+(3x-5)2-(10x-6x)(5+7x)
Tại x=-2
B=(2x+y)(y2+4x^2-2xy)-8x(x-1)(x+1)
Tại x=-2 y=3
Bài 2:
a) Ta có: \(A=\left(7x+5\right)^2+\left(3x-5\right)^2-\left(10-6x\right)\left(5+7x\right)\)
\(=\left(7x+5\right)^2+2\cdot\left(7x+5\right)\cdot\left(3x-5\right)+\left(3x-5\right)^2\)
\(=\left(7x+5+3x-5\right)^2\)
\(=\left(10x\right)^2=100x^2\)
Thay x=-2 vào A, ta được:
\(A=100\cdot\left(-2\right)^2=100\cdot4=400\)
b) Ta có: \(B=\left(2x+y\right)\left(y^2-2xy+4x^2\right)-8x\left(x-1\right)\left(x+1\right)\)
\(=8x^3+y^3-8x\left(x^2-1\right)\)
\(=8x^3+y^3-8x^3+8x\)
\(=8x+y^3\)
Thay x=-2 và y=3 vào B, ta được:
\(B=-2\cdot8+3^3=-16+27=11\)
Đúng 2
Bình luận (0)
Bài 1:
Ta có: \(A=x\left(4-x\right)\)
\(=4x-x^2\)
\(=-\left(x^2-4x\right)\)
\(=-\left(x^2-4x+4\right)+4\)
\(=-\left(x-2\right)^2+4\le4\forall x\)
Dấu '=' xảy ra khi x=2
Vậy: \(A_{max}=4\) khi x=2
Đúng 0
Bình luận (0)
Cho x,y thỏa mãn
5
x
2
+
6
x
y
+
5
y
2
16
và hàm số bậc ba y f(x) có đồ thị như hình vẽ. Gọi M, m lần lượt là giá trị lớn nhất và nhỏ nhất của
P
f
x
2
+
y...
Đọc tiếp
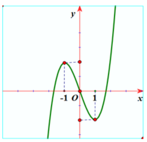
Cho x,y thỏa mãn 5 x 2 + 6 x y + 5 y 2 = 16 và hàm số bậc ba y = f(x) có đồ thị như hình vẽ. Gọi M, m lần lượt là giá trị lớn nhất và nhỏ nhất của P = f x 2 + y 2 - 2 x 2 - y 2 - 2 x y + 4 . Tính M 2 + m 2
Tìm giá trị nhỏ nhất của biểu thức:
a, 3x2 – 3x + 1
b, x2 – 2x + y2 + 4y + 6
c, 2x2 + y2 – 2xy + 1
\(a,=3\left(x^2-x+\dfrac{1}{4}\right)+\dfrac{1}{4}=3\left(x-\dfrac{1}{2}\right)^2+\dfrac{1}{4}\ge\dfrac{1}{4}\)
Dấu \("="\Leftrightarrow x=\dfrac{1}{2}\)
\(b,=\left(x^2-2x+1\right)+\left(y^2+4y+4\right)+1=\left(x-1\right)^2+\left(y+2\right)^2+1\ge1\)
Dấu \("="\Leftrightarrow\left\{{}\begin{matrix}x=1\\y=-2\end{matrix}\right.\)
\(c,=\left(x^2-2xy+y^2\right)+x^2+1=\left(x-y\right)^2+x^2+1\ge1\)
Dấu \("="\Leftrightarrow\left\{{}\begin{matrix}x=y\\x=0\end{matrix}\right.\Leftrightarrow x=y=0\)
Đúng 0
Bình luận (0)
tìm cặp số nguyên (x;y) thỏa mãn: 2x2+y2+2xy-6x-2y=8
Lời giải:
$2x^2+y^2+2xy-6x-2y=8$
$\Leftrightarrow (x^2+y^2+2xy)+x^2-6x-2y=8$
$\Leftrightarrow (x+y)^2-2(x+y)+x^2-4x=8$
$\Leftrightarrow (x+y)^2-2(x+y)+1+(x^2-4x+4)=13$
$\Leftrightarrow (x+y-1)^2+(x-2)^2=13$
$\Rightarrow (x-2)^2=13-(x+y-1)^2\leq 13$
Mà $(x-2)^2$ là scp với mọi $x$ nguyên nên $(x-2)^2\in\left\{0; 1; 4; 9\right\}$
Nếu $(x-2)^2=0\Rightarrow (x+y-1)^2=13-(x-2)^2=13$ (không là scp - loại)
Nếu $(x-2)^2=1\Rightarrow (x+y-1)^2=12$ (không là scp - loại)
Nếu $(x-2)^2=4\Rightarrow (x+y-1)^2=9$
$\Rightarrow x-2=\pm 2$ và $x+y-1=\pm 3$
TH1: $x-2=2; x+y-1=3\Rightarrow x=4; y=0$
TH2: $x-2=2; x+y-1=-3\Rightarrow x=4; y=-6$
TH3: $x-2=-2; x+y-1=3\Rightarrow x=0; y=4$
TH4: $x-2=-2; x+y-1=-3\Rightarrow x=0; y=-2$
Nếu $(x-2)^=9\Rightarrow (x+y-1)^2=4$ (bạn cũng làm tương tự trên)
Đúng 2
Bình luận (2)
1. Tìm x,y:
a) (x+2)2 + (x-3)2 = 2x ( x+ 7)
b) x3- 3x2 + 3x - 126 = 0
c) x2 + y2 - 2x + 4y + 5 = 0
d) 2x2 - 2xy + y2 + 4x + 4 = 0
\(a.\left(x^2+4x+4\right)+\left(x^2-6x+9\right)=2x^2+14x\)
\(x^2+4x+4+x^2-6x+9-2x^2-14x=0\)
\(-18x+13=0\)
\(x=\dfrac{13}{18}\)
Vậy \(S=\left\{\dfrac{13}{18}\right\}\)
\(b.\left(x-1\right)^3-125=0\)
\(\left(x-1\right)^3=125\)
\(x-1=5\)
\(x=6\)
Vậy \(S=\left\{6\right\}\)
\(c.\left(x-1\right)^2+\left(y +2\right)^2=0\)
\(Do\left(x-1\right)^2\ge0\forall x;\left(y+2\right)^2\ge0\forall y\)
\(\Rightarrow\left(x-1\right)^2+\left(y+2\right)^2\ge0\forall x,y\)
Mà \(\left(x-1\right)^2+\left(y+2\right)^2=0\)
\(\Rightarrow\left[{}\begin{matrix}\left(x-1\right)^2=0\\\left(y+2\right)^2=0\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x-1=0\\y+2=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=1\\y=-2\end{matrix}\right.\)
Vậy \(S=\left\{1;-2\right\}\)
\(d.x^2-4x+4+x^2-2xy+y^2=0\)
\(\left(x-2\right)^2+\left(x-y\right)^2=0\)
\(\Rightarrow\left[{}\begin{matrix}\left(x-2\right)^2=0\\\left(x-y\right)^2=0\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x-2=0\\x-y=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=2\\y=2\end{matrix}\right.\)
Vậy \(S=\left\{2;2\right\}\)
Đúng 0
Bình luận (0)