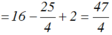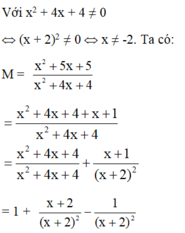Chọn B.

Ta có: 

Thay x = 4 vào A ta được:

5.4⁵ - 5.4⁴ + 5.4³ - 5.4² + 5.4 - 1

= 5.1024 - 5.256 + 5.64 - 5.16 + 5.4 - 1

= 5120 - 1280 + 320 - 80 + 20 - 1

= 4099

Kq = 4099 nha

x=4

=>x+1=5

A=(x+1)x^5 -(x+1)x^4+(x+1)x^3-(x+1)x^2+(x+1)x-1

  =x^6+x^5-x^5-x^4+x^4+x^3-x^3-x^2+x^2-x+1

  =x^6-x-1

  =4^6-4-1

  =4091

\(a,A=5\cdot4^5-5\cdot4^4+5\cdot4^3-5\cdot4^2+5\cdot4+1\\ A=4^4\left(20-5\right)+4^2\left(20-5\right)+\left(20-5\right)\\ A=15\left(4^4+4^2+1\right)=15\cdot273=4095\)

\(b,x=7\Leftrightarrow x+1=8\\ \Leftrightarrow B=x^{2006}-\left(x+1\right)x^{2005}+\left(x+1\right)x^{2004}-...+\left(x+1\right)x^2-\left(x+1\right)x-5\\ B=x^{2006}-x^{2006}-x^{2005}+x^{2005}+x^{2004}-...+x^3+x^2-x^2-x-5\\ B=-x-5=-12\)

b)tương tự

=x^2006-x^2006-x^2005+x^2005+x^2004-...+x^3-x^2-x^2-x-5

=-x-5

=-7-5=-12

`# \text {04th5}`

`a.`

`P = (5x^2 - 2xy + y^2) - (x^2 + y^2) - (4x^2 - 5xy + 1)`

`= 5x^2 - 2xy + y^2 - x^2 - y^2 - 4x^2 + 5xy - 1`

`= (5x^2 - x^2 - 4x^2) + (-2xy + 5xy) + (y^2 - y^2) - 1`

`= 3xy - 1`

`b.`

\((x^2-5x+4)(2x+3)-(2x^2-x-10)(x-3)\)

`= x^2(2x + 3) - 5x(2x + 3) + 4(2x + 3) - [ 2x^2(x - 3) - x(x - 3) - 10(x - 3)]`

`= 2x^3 + 3x^2 - 10x^2 - 15x + 8x + 12 - (2x^3 - 6x^2 - x^2 + 3x - 19x + 30)`

`= 2x^3 -7x^2 - 7x + 12 - (2x^3 - 7x^2 - 7x + 30)`

`= 2x^3 - 7x^2 - 7x + 12 - 2x^3 + 7x^2 + 7x -30`

`= -30`

Vậy, giá trị của biểu thức không phụ thuộc vào giá trị của biến.

chỗ b x = -1/2

chịuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuu

Ta có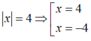

+ Trường hợp 1: x = 4 : Thay x = 4 vào biểu thức ta có:

5 . 4 2   -   2 . 4   -   18   =   5 . 16   -   8   -   18   =   80   -   8   -   18   =   54

Vậy B = 54 tại x = 4

+ Trường hợp 2: x = -4 : Thay x = -4 vào biểu thức ta có:

5 . - 4 2   - 2 . ( - 4 )   -   18   =   5 . 16   +   8   -   18   =   80   +   8   -   18   =   70

Vậy B = 70 tại x = -4

Với |x| = 4 thì B = 54 hoặc B = 70

Chọn đáp án C

1/

a)5x – 20y=5(x-4y)

b) 5x.(x –  1) –  3x(x – 1)=2x(x-1)

c) x.(x+y) – 5x – 5y=c) x.(x+y) – 5(x+y)=(x-5)(x+y)

2/

a)x² + xy + x = x(x+y+1)=77.(77+22+1)=77.100=7700

b)  x . ( x – y ) + y . ( y – x )=(x-y)(x-y)=(x-y)²=(53-3)²=2500

3/

a) X + 5x² = 0

⇒x(x+5)=0

⇒hoặc x=0

x+5=0⇒x=-5

b)x + 1 = ( x + 1 )² 

⇒(x + 1)-( x + 1 )² =0

⇒x(x+1)=0

⇒ hoặc x=0

hoặc x+1=0⇒x=-1

4/

a) 97 . 13 + 130 . 0,3 = 97.13+13.10.0,3=97.13+13.3=100.13=1300

b)86 . 153 – 530 . 8,6=86.153–53.10.8,6=86.153-53.86=86.100=8600

C) 85 .12,7 + 5,3 . 12,7= 12,7(85+5,3)=12,7.90,3=1146,81

D)52.143 – 52 . 39 – 8.26=52(143-39)-8,26=52.104-8,26=5399,74

Bài 1:  

a) 5x-20y=5(x-4y)

b) \(5x\left(x-1\right)-3x\left(x-1\right)=2x\left(x-1\right)\)

c) \(x\left(x+y\right)-5x-5y=\left(x+y\right)\left(x-5\right)\)

Bài 2: 

a) \(x^2+xy+x\)

\(=x\left(x+y+1\right)\)

\(=77\cdot\left(77+22+1\right)\)

=7700

b) \(x\left(x-y\right)+y\left(y-x\right)\)

\(=x\left(x-y\right)-y\left(x-y\right)\)

\(=\left(x-y\right)^2\)

\(=50^2=2500\)