CMR:301293-1⋮13
làm bằng pp đồng dư
Tìm số dư khi:
a, 3100 : 7
b, 301293 : 13
Cmr:
\(2^{4n+1}\)-2 ⋮ 15
(chứng minh bằng đồng dư)
\(A=2^{4n+1}-2\)
\(=2\left(2^{4n}-1\right)\)
\(=2\left(16^n-1\right)\)
\(=2\left(16-1\right)\left(16^{n-1}+16^{n-2}+...+16^0\right)\)
=>\(A⋮\left(16-1\right)\)
=>A chia hết cho 15
CMR:
a) Nếu a đồng dư 1 (mod2) thì a^2 đồng dư 1 (mod 8)
b) Nếu a đồng dư 1(mod 3) thì a^3 đồng dư 1 (mod9)
bài 1 CMR:
a,(1991^1997-1997^1996) chia hết cho 10
b,(2^9+2^99) chia hết cho 100
bài 2 CMR
a,nếu a đồng dư1(mod2)thì a^2 đồng dư 1(mod8)
b, nếu a đồng dư 1(mod3) thì a^3 đồng dư 1(mod9)
bài này vượt quá giới hạn của ta rồi
Câu 1 cách làm:
Cậu có thể đưa ra chữ số tận cùng của mỗi lũy thừa, ví dụ như thế này để tính
2^(4k+1) có tận cùng là 2 nên 2^2009 có tận cùng là 2(2009=4.502+1)
Tách kim loại đồng dạng bột ra khỏi hh bột đồng, sắt. Bằng pp vật lí và pp hoá học. Viết PTHH nếu có
ta cho nam châm :
sắt bị nam châm hút
còn lại là đồng
>
ta cho hỗn hợp vào HCl
sắt tan , ta gạn dd , sấy khô thu đc Cu
dung dichj thu đc ta cho vào NaOH-> có kết tủa
sau đó ta nung nóng và dẫn khí H2 vào ta thu đc Fe tinh khiết
Fe+HCl->FeCl2+H2
FeCl2+2NaOH->Fe(OH)2+2NaCl
Fe(OH)2-to->FeO+H2O
FeO+H2-to->Fe+H2O
PP vật lí
- Đưa nam châm vào hỗn hợp Cu và Fe
=> Cu ko bị nam châm hút,Fe bị nam châm hút
=> Tách đc hai bột Fe và đồng
PP hoá học
- Cho hỗn hợp 2 bột vào dung dịch HCl dư,sau p/ứ lọc lấy chất rắn ko tan => Đó là Cu
PTHH Fe+2HCl->FeCl2+H2
- Đem dung dịch nước lọc thu được cho dung dịch NaOH dư vào
=> Thu được chất rắn ko tan là Fe(OH)2
PTHH
FeCl2+2NaOH->Fe(OH)2↓+2NaCl
- Đem Fe(OH)2 đi nhiệt phân ở nhiệt độ cao,sau đó cho 1 luồng khí H2 dư đi qua
=> Thu được Fe
PTHH
4Fe(OH)2+O2-(to)->2Fe2O3+4H2O
Fe2O3+3H2-(to)->2Fe+3H2O
Cho aϵZ. CMR:
a) Nếu a đồng dư 1 (mod 2) thì a2 đồng dư 1 (mod 8).
b) Nếu a đồng dư 1 (mod 3) thì a3 đồng dư 1 (mod 9)
Lời giải:
a)
$a\equiv 1\pmod 2$ nên $a$ có dạng $2k+1$ $(k\in\mathbb{Z}$
Khi đó:
$a^2=(2k+1)^2=4k^2+4k+1=4k(k+1)+1$
Vì $k(k+1)$ là tích 2 số nguyên liên tiếp nên $k(k+1)\vdots 2$
$\Rightarrow 4k(k+1)\vdots 8$
$\Rightarrow a^2=4k(k+1)+1$ chia $8$ dư $1$ hay $a^2\equiv 1\pmod 8$
b)
$a\equiv 1\pmod 3\Rightarrow a-1\equiv 0\pmod 3(1)$ hay
Lại có:
$a\equiv 1\pmod 3\Rightarrow a^2+a+1\equiv 1+1+1\equiv 0\pmod 3(2)$
Từ $(1);(2)\Rightarrow (a-1)(a^2+a+1)\equiv 0\pmod 9$
hay $a^3-1\equiv 0\pmod 9\Leftrightarrow a^3\equiv 1\pmod 9$
CMR: \(3+\text{3}^{\text{2}}\text{+3}^{\text{3}}+...+3^{100}\)⋮120 bằng đồng dư thức
Cách này không dùng đồng dư thức.
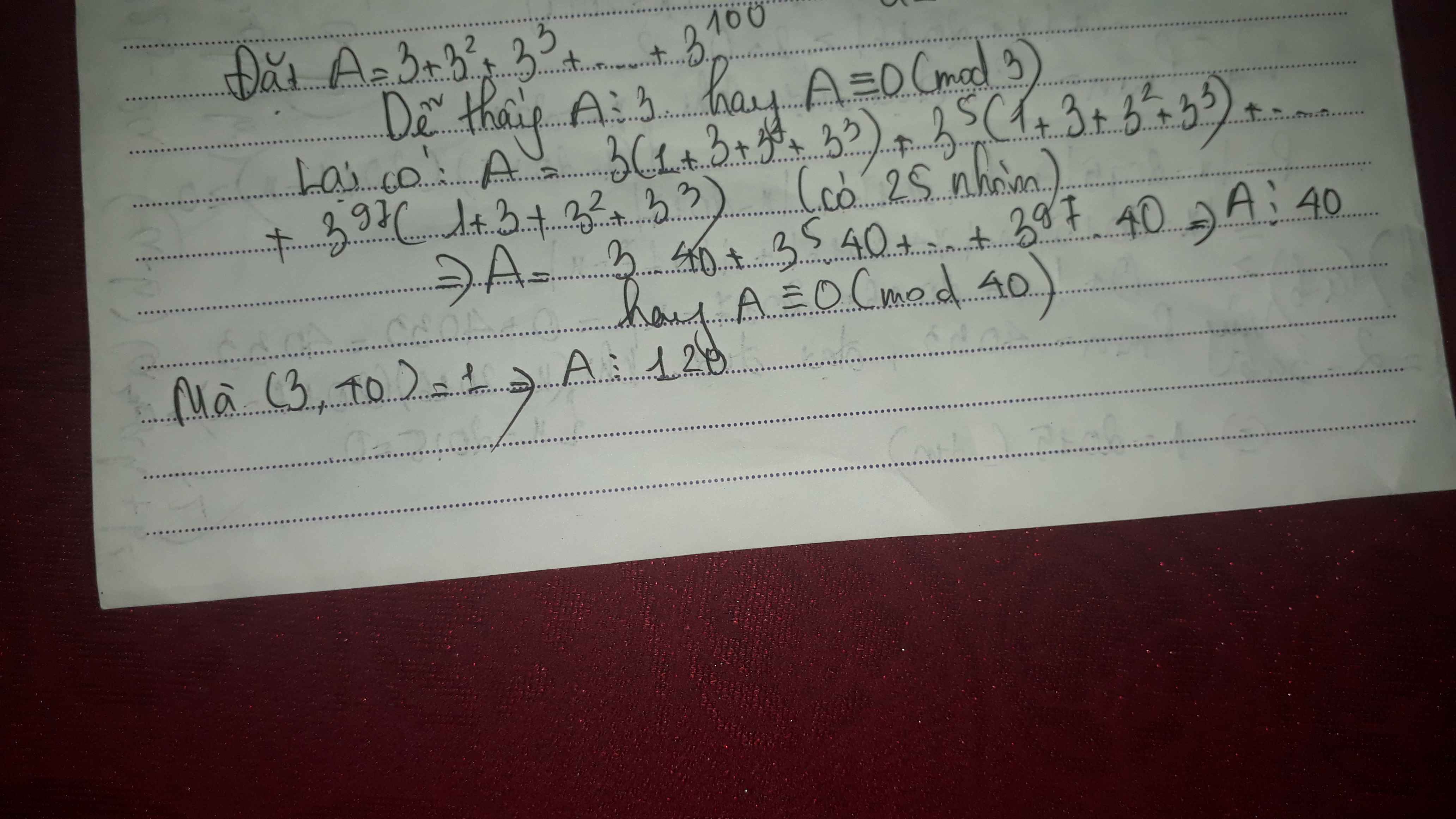
phân tích thành nhân tử bằng pp chia 3 dư 2 chia 3 dư 1
x^4+x^2 -30
x^7+x^5+1
x^8+x^7+1
Ai help mik sẽ tick
1,tìm số dư của 1994^2005:7
2,cmr :6^1001-1 và 6^1001+1 đều chia hết cho7
3,tìm số dư trong phép chia 1532^5-1:9
4,tìm số dư trong phép chia 3^2003:13
5,tìm số dư trong phép chia 7.5^2n+12.6^n:19 (n thuộc N)
Giải bằng phép đồng dư
cho n là số dương CMR:
a) 2+4+6+...+2n=n(n+1)
b) 1^3+3^3+5^3+...+(2n-1)^3=2n(2n^2-1)
chứng minh bằng PP quy nạp