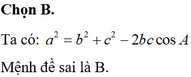cho tam giá ABC, có a=7,b=8,c=10 tìm độ dài đường trung tuyến kẻ từ A

Những câu hỏi liên quan
Cho tam giác ABC biết a = sqrt(3) b = 2 ; tilde C =30^
a) Tính độ dài cạnh b ,c
b) Tính diện tích tam giác ABC và độ dài đường trung tuyến m_{a} kẻ từ đinh A của tam giác ABC
a: Xét ΔCAB có \(cosC=\dfrac{CA^2+CB^2-AB^2}{2\cdot CA\cdot CB}\)
=>\(\dfrac{2^2+3-AB^2}{2\cdot2\cdot\sqrt{3}}=cos30=\dfrac{\sqrt{3}}{2}\)
=>\(7-AB^2=4\sqrt{3}\cdot\dfrac{\sqrt{3}}{2}=2\cdot3=6\)
=>AB=1
b: Xét ΔABC có \(AB^2+BC^2=CA^2\)
nên ΔABC vuông tại B
=>\(S_{BAC}=\dfrac{1}{2}\cdot BA\cdot BC=\dfrac{1}{2}\cdot1\cdot\sqrt{3}=\dfrac{\sqrt{3}}{2}\)
Độ dài đường trung tuyến kẻ từ A là:
\(m_A=\sqrt{\dfrac{b^2+c^2}{2}-\dfrac{a^2}{4}}=\sqrt{\dfrac{4+1}{2}-\dfrac{3}{4}}=\dfrac{\sqrt{7}}{2}\)
Đúng 0
Bình luận (0)
Cho tam giác ABC cân tại A có đường trung tuyến AM.
a) Chứng minh A M ⊥ B C .
b) Biết AB = 10 cm, BC = 12 cm. Tính độ dài đoạn vuông góc kẻ từ B xuống AC.
Cho tam giác ABC cân ở A, đường trung tuyến AM.
a) Chứng minh AM BC
b) Tính AM biết rằng AB cm BC cm 10 , 12
Đúng 0
Bình luận (0)
Trong mặt phẳng với hệ tọa độ Oxy, cho tam giác ABC có đỉnh A(2;1), trực tâm H(14;-7) đường trung tuyến kẻ từ đỉnh B có phương trình (d):
9x - 5y - 7=0. Tìm tọa độ các đỉnh B, C.
Cho tam giác ABC có C(-1;-2),đường trung tuyến kẻ từ A và đường cao kẻ tù B lần lượt có phương trình là 5x+y-9=0 và x+3y-5=0. Tìm tọa độ A và B
Cho tam giác ABC, có độ dài ba cạnh là BCa,ACb,ABc. Gọi
m
a
là độ dài đường trung tuyến kẻ từ đỉnh A, R là bán kính đường tròn ngoại tiếp tam giác và S là diện tích tam giác đó. Mệnh đề nào sau đây sai? A.
m
a
2
b
2
+
c
2
2
-...
Đọc tiếp
Cho tam giác ABC, có độ dài ba cạnh là BC=a,AC=b,AB=c. Gọi m a là độ dài đường trung tuyến kẻ từ đỉnh A, R là bán kính đường tròn ngoại tiếp tam giác và S là diện tích tam giác đó. Mệnh đề nào sau đây sai?
A. m a 2 = b 2 + c 2 2 - a 2 4
B. a 2 = b 2 + c 2 + 2 b c cos A
C. S = a b c 4 R
D. a sin A = b sin B = c sin C = 2 R
Tam giác ABC có AB = 6 ; AC = 8 và BC = 10. Độ dài đường trung tuyến xuất phát từ đỉnh A của tam giác bằng:
A. 3
B. 6
C. 7
D. 5
Chọn D.
Cách 1: Áp dụng công thức đường trung tuyến ![]() ta được:
ta được:
![]()
Suy ra ma = 5
Cách 2: nhận xét đây là tam giác vuông tại A nên ma = 1/2. BC = 5.
Đúng 0
Bình luận (0)
Cho tam giác ABC có A(1;1), B(2;2),C(3;-1) a.Viết phương trình tổng quát BC b.Viết phương trình tổng quát đường cao AH c. Viết phương trình tổng quát của trung tuyến kẻ từ B. d. Tính độ dài đường cao kẻ từ A e. Viết phương trình đường thẳng đi qua B và chia tam giác ABC thành 2 denta có cùng diện tích.
a: vecto BC=(1;-3)
=>VTPT là (3;1)
Phương trình BC là:
3(x-2)+y-2=0
=>3x-6+y-2=0
=>3x+y-8=0
b: Phương trình AH nhận vecto BC làm VTPT
=>Phương trình AH là:
1(x-1)+(-3)*(y-1)=0
=>x-1-3y+3=0
=>x-3y+2=0
c: Tọa độ M là:
\(\left\{{}\begin{matrix}x=\dfrac{1+3}{2}=2\\y=\dfrac{1-1}{2}=0\end{matrix}\right.\)
M(2;0); B(2;2)
vecto BM=(0;-2)
=>VTPT là (2;0)
Phương trình BM là:
2(x-2)+0(y-0)=0
=>2x-4=0
=>x=2
Đúng 0
Bình luận (0)
Cho tam giác ABC có đường cao kẻ từ A, đường trung tuyến xuất phát từ B và đường phân giác kẻ từ đỉnh C đồng qui. Gọi a, b, c lần lượt là độ dài 3 cạnh BC, AC, AB. Chứng minh (a + b)(a2 + b2 - c2) = 2a2b
Câu 1:Cho tam giác ABC có B (2;1), đường cao và trung tuyến kẻ từ 1đỉnh A là x-y+2=9,2x-3y+1=0. tìm C,A
Câu 2:Cho tam giác ABC có B (4;2), đường trung tuyến từ A x+ y-1=0,AC:2x-y+3=0.Tim phương trình C
Xem chi tiết
1.
Tọa độ A là nghiệm: \(\left\{{}\begin{matrix}x-y+2=0\\2x-3y+1=0\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}x=-5\\y=-3\end{matrix}\right.\)
\(\Rightarrow A\left(-5;-3\right)\)
Phương trình BC qua B và vuông góc đường cao kẻ từ A có dạng:
\(1\left(x-2\right)+1\left(y-1\right)=0\Leftrightarrow x+y-3=0\)
Gọi M là trung điểm BC thì tọa độ M thỏa mãn:
\(\left\{{}\begin{matrix}2x-3y+1=0\\x+y-3=0\end{matrix}\right.\) \(\Rightarrow M\left(\dfrac{8}{5};\dfrac{7}{5}\right)\)
M là trung điểm BC \(\Rightarrow C\left(\dfrac{6}{5};\dfrac{9}{5}\right)\)
2.
Do C thuộc AC nên tọa độ có dạng: \(C\left(c;2c+3\right)\)
Gọi M là trung điểm BC \(\Rightarrow M\left(\dfrac{c+4}{2};\dfrac{2c+5}{2}\right)\)
M thuộc trung tuyến kẻ từ A nên:
\(\dfrac{c+4}{2}+\dfrac{2c+5}{2}-1=0\Leftrightarrow c=-\dfrac{7}{3}\)
\(\Rightarrow C\left(-\dfrac{7}{3};-\dfrac{5}{3}\right)\)
Đúng 0
Bình luận (0)
Cho tam giác ABC có A( -3; 7) ; B( 0; 8) ; C(-1; -4).
a) Viết phương trình của đường thẳng AB.
b) Tính độ dài đường cao kẻ từ C.
c) Tính \(\widehat{C}\) của \(\Delta\)ABC
a, \(\overrightarrow{AB}=\left(3;1\right)\)
Phương trình đường thẳng AB:
\(\dfrac{x+3}{3}=\dfrac{y-7}{1}\Leftrightarrow x-3y+24=0\)
b, \(d\left(C,AB\right)=\dfrac{\left|-1-3.\left(-4\right)+24\right|}{\sqrt{1^2+3^2}}=\dfrac{7\sqrt{10}}{2}\)
c, \(AB=\sqrt{10};BC=\sqrt{145};CA=\sqrt{137}\)
Theo định lí hàm số cosin: \(cosC=\dfrac{BC^2+AC^2-AB^2}{2.BC.AC}=...\)
Đúng 0
Bình luận (0)