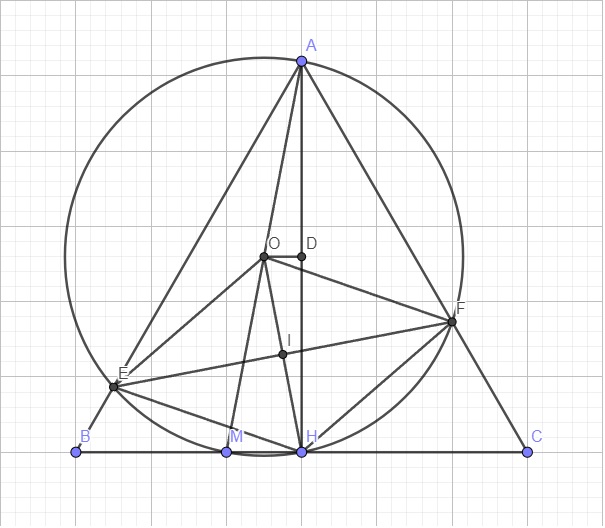
Cho△ABC vuông tại A,đường cao AH.Từ M là điểm bất kì trên cạnh BC kẻ MD⊥AB,ME⊥AC.Chứng minh 5 điểm A,D,M,H,E cùng nằm trên 1 đường tròn

Những câu hỏi liên quan
cho tam giác abc vuông tại a đường cao ah từ m là một điểm bất kì trên cạnh bc kẻ md vuông góc với ab, me vuông góc với ac chứng minh 5 điểm a,d,m,h,e cùng nằm trên một đường tròn
cho tam giác abc vuông tại a đường cao ah từ m là một điểm bất kì trên cạnh bc kẻ md vuông góc với ab, me vuông góc với ac chứng minh 5 điểm a,d,m,h,e cùng nằm trên một đường tròn
Cho tam giác ABC vuông tại A, đường cao AH. Từ M là điểm bất kỳ trên cạnh BC.
Kẻ MD AB,ME AC . Chứng minh 5 điểm A,D,M,H,E cùng nằm trên một đường tròn.
Ta có:AH\(\perp\)BC
=>\(AH\perp\)HM
=>\(\widehat{AHM}=90^0\)
Ta có: \(\widehat{AEM}=\widehat{ADM}=\widehat{AHM}=90^0\)
=>A,E,M,H,D cùng thuộc đường tròn đường kính AH
Đúng 0
Bình luận (0)
Cho tam giác ABC \(\left(A=90^0\right)\), đường cao AH. Từ điểm M bất kì trên cạnh BC kẻ \(MD\perp AB\), \(ME\perp AC\). Chứng minh năm điểm A, D, M, H, E cùng nằm trên một đường tròn
em tự vẽ hình nha
Gọi O là trung điểm của AM
Vì tam giác AHM vuông tại H có O là trung điểm cạnh huyền AM
=> OH=OA=OM (1)
CMTT: OA=OM=OE (2)
Vì \(\hept{\begin{cases}MD\perp AB\\ME\perp AC\end{cases}\Rightarrow}\hept{\begin{cases}\widehat{MDA}=90^0\\\widehat{MEA}=90^0\end{cases}}\)
Xét tứ giác ADME có:
góc A= góc MDA = góc MEA = 90 độ
=> ADME là hình chữ nhật ( dhnb )
=> 2 đường chéo DE và AM cắt nhau tại trung điểm mỗi đường và DE=AM
Mà O là trung điểm AM
=> O là trung điểm DE
=> OD=OE (3)
Từ (1), (2) và (3) => OD=OE=OA=OM=OH
=> A,D,H,M,F cùng nằm trên 1 đường tròn
cho tam giác ABC vuông tại A ; AH vuông góc BC; M là điểm bất kì trên BC kẻ MD vuông góc AB(D thuộc AB ); ME vuông góc AC (E thuộc AC) gọi I là trung điểm DE hãy chứng minh I nằm trên đường trung trực của AH
Cho tam giác đều ABC cạnh a với đường cao AH. M là 1 điểm bất kì trên cạnh BC. Vẽ ME vuông góc AB, MF vuông góc AC. Gọi O là trung điểm của AM.
a). CM rằng 5 đ A, E, H, M, F cùng nằm trên cùng một đường tròn.
b). Tứ giác OEHF là hình gì.
c). Tìm GTNN của diện tích tứ giác OEHF theo a khi M di động trên cạnh BC.
(Nếu được thì giải chi tiết câu (c) giúp em em cảm ơn ạ)
a. Em tự giải
b. Do tam giác ABC đều và AH là đường cao \(\Rightarrow AH\) đồng thời là phân giác góc A
\(\Rightarrow\widehat{BAH}=\widehat{CAH}=\dfrac{1}{2}\widehat{A}=\dfrac{1}{2}.60^0=30^0\)
AEMHF nội tiếp đường tròn tâm O \(\Rightarrow\widehat{HOF}=2.\widehat{CAH}=60^0\) (góc nội tiếp và góc ở tâm cùng chắn cung HF)
Mà \(OH=OF\) (cùng là bán kính) \(\Rightarrow\Delta OHF\) đều (tam giác cân có 1 góc 60 độ)
Tương tự ta có \(\widehat{HOE}=60^0\Rightarrow\Delta OHE\) đều
\(\Rightarrow OE=OF=HE=HF\Rightarrow OEHF\) là hình thoi
c.
Gọi D là trung điểm AH \(\Rightarrow OD\perp AH\) \(\Rightarrow OH\ge DH\Rightarrow OH\ge\dfrac{1}{2}AH\Rightarrow OH\ge\dfrac{a\sqrt{3}}{2}\)
Gọi I là giao điểm EF và OH \(\Rightarrow I\) là tâm hình thoi OEHF
\(S_{OEHF}=2S_{OHE}=2EI.OH=2\sqrt{OE^2-OI^2}.OH\)
\(=2OH.\sqrt{OH^2-\left(\dfrac{OH}{2}\right)^2}=OH^2\sqrt{3}\ge\left(\dfrac{a\sqrt{3}}{2}\right)^2.\sqrt{3}=\dfrac{3a^2\sqrt{3}}{2}\)
Dấu "=" xảy ra khi \(OH=DH\Leftrightarrow O\) trùng D
\(\Rightarrow M\) trùng H
Đúng 3
Bình luận (4)
- cho tam giác ABC vuông tại A , kẻ AH vuông góc với BC tại H . Trên cạnh BC lấy điểm M ( M khác B, C , H ) . Kẻ ME vuông góc với AB tại E , MF vuông góc với AC tại F
- 1) chứng minh các điểm A,E,F,H cùng nằm trên một đường tròn
- 2) chứng minh BE.CF= ME.MF
1)Xét tứ giác EMAF có 3 goc vg => AEMF la hcn => các điểm A,E,F,H cùng nằm trên một đường tròn
2)
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
Cho tam giác ABC cân tại A, BH vuông góc AC tại H. Trên cạnh BC lấy điểm M bất kì (M khác B và C). Gọi D, E, F là chân đường vuông góc hạ từ M đến AB, AC, BH.
a) Chứng minh: ∆DBM = ∆FMB.
b) Chứng minh khi M chạy trên cạnh BC thì tổng MD + ME có giá trị không đổi.
c) Trên tia đối của tia CA lấy điểm K sao cho CK = EH.
Chứng minh: BC đi qua trung điểm của đoạn thẳng DK.
Cho tam giác ABC cân tại A, BH vuông góc AC tại H. Trên cạnh BC lấy điểm M bất kì (M khác B và C). Gọi D, E, F là chân đường vuông góc hạ từ M đến AB, AC, BH.
a) Chứng minh: ∆DBM = ∆FMB.
b) Chứng minh khi M chạy trên cạnh BC thì tổng MD + ME có giá trị không đổi.
c) Trên tia đối của tia CA lấy điểm K sao cho CK = EH.
Chứng minh: BC đi qua trung điểm của đoạn thẳng DK.
a: Xét ΔDBM vuông tại D và ΔFMB vuông tại F có
MB chung
góc DBM=góc FMB
=>ΔDBM=ΔFMB
b:
Xét tứ giác FHEM có
FH//EM
FM//HE
=>FHEM là hình bình hành
MD+ME=FB+FH=BH ko đổi
Đúng 0
Bình luận (0)
Cho đường tròn (O;R) và một đường thẳng d cắt (O) tại C,D. Một điểm M bất kì trên d sao cho MC>MD và nằm ngoài đường tròn. Qua M kẻ MA vuông góc với OA tại A; kẻ MB vuông góc với OB tại B. Gọi H là trung điểm CD; AB cắt MO, OH tại E,F. Chứng minh
a, OE.OM=R2
b, M,E,H,F cùng thuộc một đường tròn
c, Điểm F cố định khi M di chuyển