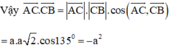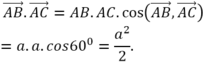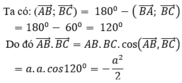cho tam giác ABC, AB=5, BC=7, CA=8. tính tích vô hướng của AB nhân AC

Những câu hỏi liên quan
Trong tọa độ Oxy, Cho tam giác ABC với A(2:-3),B(4:7),C(-3:2) a) tìm tọa độ vecto AB, vecto AC, vecto BC b) tính tích vô hướng của vecto AB.BC và vecto AB.AC c) tính góc tạo bởi các vecto AB và AC, AB vad BC d) tính chu vi của tam giác ABC
\(a,\overrightarrow{AB}=\left(2;10\right)\)
\(\overrightarrow{AC}=\left(-5;5\right)\)
\(\overrightarrow{BC}=\left(-7;-5\right)\)
\(b,\) Thiếu dữ kiện
\(c,Cos\left(\overrightarrow{AB},\overrightarrow{AC}\right)=\dfrac{\left|2\left(-5\right)+10.5\right|}{\sqrt{2^2+10^2}.\sqrt{\left(-5\right)^2+5^2}}=\dfrac{2\sqrt{13}}{13}\)
\(\Rightarrow\left(\overrightarrow{AB},\overrightarrow{AC}\right)=56^o18'\)
\(Cos\left(\overrightarrow{AB},\overrightarrow{BC}\right)=\dfrac{\left|2\left(-7\right)+10\left(-5\right)\right|}{\sqrt{2^2+10^2}.\sqrt{\left(-7\right)^2+\left(-5\right)^2}}\)
\(\Rightarrow\left(\overrightarrow{AB},\overrightarrow{BC}\right)=43^o9'\)
Đúng 0
Bình luận (0)
Cho tam giác vuông cân ABC cạnh huyền bằng a. khi đó giá trị của biểu thức tích vô hướng
A
B
→
.
B
C
→
+
B
C
→
.
C
A
→
+
C
A
→
.
A
B...
Đọc tiếp
Cho tam giác vuông cân ABC cạnh huyền bằng a. khi đó giá trị của biểu thức tích vô hướng A B → . B C → + B C → . C A → + C A → . A B → là
A. 0
B. - a 2
C. - 2 a 2
D. 2 a 2
A B → + B C → + C A → 2 = A B → 2 + B C → 2 + C A → 2 + 2. ( A B → . B C → + B C → . C A → + C A → . A B → ) ⇔ 2. ( A B → . B C → + B C → . C A → + C A → . A B → ) = A B → + B C → + C A → 2 = − A B → 2 − B C → 2 − C A → = 0 → 2 − A B 2 − B C 2 − C A 2 = 0 − a 2 − a 2 = − 2 a 2 ⇔ A B → . B C → + B C → . C A → + C A → . A B → = − a 2
Đáp án B
Đúng 0
Bình luận (0)
Cho tam giác ABC có AB = 5, BC = 6 và AC = 9. Gọi M là trung điểm của BC, N là điểm thuộc cạnh AC sao cho AC = 3NC. Tính tích vô hướng \(\overrightarrow{AM}.\overrightarrow{BN}\).
Cho tam giác ABC vuông cân tại A, có cạnh huyền bằng \(\sqrt 2 \).
Tính các tích vô hướng: \(\overrightarrow {AB} .\overrightarrow {AC} ,\overrightarrow {AC} .\overrightarrow {BC} ,\overrightarrow {BA} .\overrightarrow {BC} \)

+) Ta có: \(AB \bot AC \Rightarrow \overrightarrow {AB} \bot \overrightarrow {AC} \Rightarrow \overrightarrow {AB} .\overrightarrow {AC} = 0\)
+) \(\overrightarrow {AC} .\overrightarrow {BC} = \left| {\overrightarrow {AC} } \right|.\left| {\overline {BC} } \right|.\cos \left( {\overrightarrow {AC} ,\overrightarrow {BC} } \right)\)
Ta có: \(BC = \sqrt {A{B^2} + A{C^2}} = \sqrt 2 \Leftrightarrow \sqrt {2A{C^2}} = \sqrt 2 \)\( \Rightarrow AC = 1\)
\( \Rightarrow \overrightarrow {AC} .\overrightarrow {BC} = 1.\sqrt 2 .\cos \left( {45^\circ } \right) = 1\)
+) \(\overrightarrow {BA} .\overrightarrow {BC} = \left| {\overrightarrow {BA} } \right|.\left| {\overrightarrow {BC} } \right|.\cos \left( {\overrightarrow {BA} ,\overrightarrow {BC} } \right) = 1.\sqrt 2 .\cos \left( {45^\circ } \right) = 1\)
Đúng 0
Bình luận (0)
Cho tam giác đều ABC có cạnh bằng a. Tính tích vô hướng
A
B
→
.
A
C
→
.
A.
A
B
→
.
A
C
→
2
a
2
.
B. ...
Đọc tiếp
Cho tam giác đều ABC có cạnh bằng a. Tính tích vô hướng A B → . A C → .
A. A B → . A C → = 2 a 2 .
B. A B → . A C → = − a 2 3 2 .
C. A B → . A C → = − a 2 2 .
D. A B → . A C → = a 2 2 .
Ta có: góc A B → , A C → là góc A ^ nên A B → , A C → = 60 0 .
Do đó A B → . A C → = A B . A C . c o s A B → , A C → = a . a . c o s 60 0 = a 2 2 .
Chọn D.
Đúng 0
Bình luận (0)
Cho tam giác vuông cân ABC có AB = AC = a. Tính các tích vô hướng 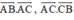
Cho tam giác đều ABC có cạnh bằng a. Tính tích vô hướng
A
B
→
.
A
C
⇀
A. 2a2 B. a2 C. - a2 D.
a
2
2
Đọc tiếp
Cho tam giác đều ABC có cạnh bằng a. Tính tích vô hướng A B → . A C ⇀
A. 2a2
B. a2
C. - a2
D. a 2 2
Cho tam giác đều ABC có cạnh bằng a. Tính tích vô hướng
A
B
→
.
B
C
→
A. B. C. D.
Đọc tiếp
Cho tam giác đều ABC có cạnh bằng a. Tính tích vô hướng A B → . B C →
A. ![]()
B. ![]()
C. ![]()
D. ![]()
Cho tam giác ABC vuông cân tại A , có AB = AC = 2. Gọi M,N lần lượt là trung điểm của AB và AC . Tính tích vô hướng của BM và CN.