cho ab//bc, ab=cd, ab cắt bc tại o. C/m tam giác oab bằng tam giác ocd

Những câu hỏi liên quan
Cho tam giác OAB cân tại O. Gọi C và D lần lượt trên 2 cạnh OA và Ob. Sao cho AD vuông góc với OB và BC vuông góc với OA. CMR
a AD=BC và tam giác OCD cân
b Gọi M là giao điểm của BC và AD. CMR OM vuông góc vs AB, OM là tia phân giác góc O
c Chứng minh MA=MB
d CM AB//CD
Cho hình thang cân ABCD(AB//CD).AB6cm,CD10cm.AD cắt BC tại O a)Chứng minh tam giác OAB cân b)Gọi M,N lần lượt là trung điểm của AD và BC tính MN.
Đọc tiếp
Cho hình thang cân ABCD(AB//CD).AB=6cm,CD=10cm.AD cắt BC tại O
a)Chứng minh tam giác OAB cân
b)Gọi M,N lần lượt là trung điểm của AD và BC tính MN.
a) Ta có: AB//CD(ABCD là hthang cân)
\(\Rightarrow\left\{{}\begin{matrix}\widehat{OAB}=\widehat{ODC}\\\widehat{OBA}=\widehat{OCD}\end{matrix}\right.\)
Mà \(\widehat{ODC}=\widehat{OCD}\)(ABCD là hthang cân)
\(\Rightarrow\widehat{OBA}=\widehat{OAB}\)
=> Tam giác OAB cân tại O
b) Xét hthang ABCD có:
M là trung điểm AD(gt)
N là trung điểm BC(gt)
=> MN là đường trung bình
=> \(MN=\dfrac{AB+CD}{2}=\dfrac{6+10}{2}=8\left(cm\right)\)
Đúng 0
Bình luận (1)
\(a,AB//CD\Rightarrow\widehat{A_1}=\widehat{D};\widehat{B_1}=\widehat{C}\left(so.le.trong\right)\)
Mà \(\widehat{C}=\widehat{D}\left(hthang.cân.ABCD\right)\)
\(\Rightarrow\widehat{A_1}=\widehat{B_1}\)
Vậy tam giác OAB cân tại O
\(b,\left\{{}\begin{matrix}AM=MD\\BN=NC\end{matrix}\right.\Rightarrow MN\) là đtb hình thang ABCD
\(\Rightarrow MN=\dfrac{1}{2}\left(AB+CD\right)=8\left(cm\right)\)
Đúng 1
Bình luận (2)
a: Ta có: \(\widehat{OAB}=\widehat{ODC}\)
\(\widehat{OBA}=\widehat{OCD}\)
mà \(\widehat{ODC}=\widehat{OCD}\)
nên \(\widehat{OAB}=\widehat{OBA}\)
hay ΔOAB cân tại O
b: Xét hình thang ABCD có
M là trung điểm của AD
N là trung điểm của BC
Do đó: MN là đường trung bình của hình thang ABCD
Suy ra: \(MN=\dfrac{AB+CD}{2}=8\left(cm\right)\)
Đúng 0
Bình luận (0)
bài 1: cho hình thang vuông ABCD (vuông tại A và D ) có 2 đường chéo vuông góc với nhau tại O , AB=4cm , CD=9cm.
a) CMR : tam giác OAB đồng dạng với tam giác DAB
b) Tính độ dài AD
c) CM : tam giác OAB đồng dạng với tam giác OCD
d) Tính tỉ số diện tích của tam giác OAB và OCD
a) Xét tam giác AOD và tam giác BAD có:
{Dˆ:chungAOˆD=DAˆB=90{D^:chungAO^D=DA^B=90⇒ΔAOD≀ΔBAD(g.g)⇒ΔAOD≀ΔBAD(g.g)
b) Ta có: DAˆO=ABˆD=ABˆO(ΔAOD≀ΔBAD)DA^O=AB^D=AB^O(ΔAOD≀ΔBAD)
Và AOˆD=AOˆB=90AO^D=AO^B=90 (2 đường chéo vuông góc tại O)
Do đó ΔAOD≀ΔBOA(g.g)ΔAOD≀ΔBOA(g.g)
⇒ADAB=ODAO⇒ADAB=ODAO (1)
Lại có: {DAˆO:chungAOˆD=ADˆC=90{DA^O:chungAO^D=AD^C=90⇒ΔADC≀ΔAOD(g.g)⇒ΔADC≀ΔAOD(g.g)
⇒CDOD=ADAO⇔CDAD=ODAO⇒CDOD=ADAO⇔CDAD=ODAO (2)
Từ (1);(2)⇒ADAB=CDAD⇒AD2=AB⋅CD⇒ADAB=CDAD⇒AD2=AB⋅CD
c) Ta có: AB song song với DC (ABCD là hình thang)
⇒ABˆO=ODˆC(slt)⇒AB^O=OD^C(slt)
Và AOˆB=DOˆC(đ2)AO^B=DO^C(đ2)
Do đó ΔOCD≀ΔOAB(g.g)ΔOCD≀ΔOAB(g.g)
⇒k=OCOA=CDAB=94⇒k=OCOA=CDAB=94
⇒SΔOCDSΔOAB=k2=942=8116⇒SΔOCDSΔOAB=k2=942=8116
Vậy........................
Δ : tam giác. Chúc bạn học tốt nhé!
Đúng 0
Bình luận (0)
cho hình thang vuông ABCD (vuông tại A và D ) có 2 đường chéo vuông góc với nhau tại O , AB=4cm , CD=9cm.
a) CMR : tam giác OAB đồng dạng với tam giác DAB
b) Tính độ dài AD
c) CM : tam giác OAB đồng dạng với tam giác OCD
d) Tính tỉ số diện tích của tam giác OAB và OCD
bạn ơi bạn làm đc bài này chưa cho mình lời giải với
Đúng 0
Bình luận (0)
Chú ý :Δ là tam giác
a) Xét ΔAOD và ΔBAD có:
{Dˆ:chungAOˆD=DAˆB=90⇒ΔAOD≀ΔBAD(g.g)
b) Ta có: DAˆO=ABˆD=ABˆO(ΔAOD≀ΔBAD)
Và AOˆD=AOˆB=90 (2 đường chéo vuông góc tại O)
Do đó ΔAOD≀ΔBOA(g.g)
⇒ADAB=ODAO (1)
Lại có: {DAˆO:chungAOˆD=ADˆC=90⇒ΔADC≀ΔAOD(g.g)
⇒CDOD=ADAO⇔CDAD=ODAO (2)
Từ (1);(2)⇒ADAB=CDAD⇒AD2=AB⋅CD
c) Ta có: AB song song với DC (ABCD là hình thang)
⇒ABˆO=ODˆC(slt)
Và AOˆB=DOˆC(đ2)
Do đó ΔOCD≀ΔOAB(g.g)
⇒k=OCOA=CDAB=94
⇒SΔOCDSΔOAB=k2=942=8116
Vậy........................
Chúc bạn học tốt nhé !
Đúng 0
Bình luận (0)
Cho tam giác AOB trên tia đối của tia OA lấy điểm C sao cho OA =OC.TRên tia đối của tia OB lấy điểm D sao cho OB=OD .Các tia phân giác của các góc OCD và OBA cắt nhau ở E .tia phân giác của góc OAB cắt BE tại F
a) CMR: tam giác AOB bằng tam giác COD
b) CMR : AB//CD; AD//BC; CE//AF
c)góc CEB bằng 1/2 của tổng hai góc CAB và CDB
a,Xét \(\Delta AOB\)và \(\Delta COD\)có :
\(OC=OA\)(gt)
\(OD=OB\)(gt)
\(O_1=O_2\)(đối đỉnh)
\(=>\Delta AOB=\Delta COD\left(c-g-c\right)\)
b,Ta có :\(DCO=BAO\)(cm câu a)
Do 2 góc này ở vị trí so le trong và bằng nhau
\(=>AB//CD\)
Xét \(\Delta DAO\)và \(\Delta BCO\)có :
\(OC=OA\)(gt)
\(OB=OD\)(gt)
\(COB=AOD\)(đối đỉnh)
\(=>\Delta DAO=\Delta BCO\left(c-g-c\right)\)
\(=>ODA=OBC\)(2 góc tương ứng)
Do 2 góc này ở vị trí so le trong và bằng nhau
\(=>DA//BC\)
Gọi giao điểm của CE và DO là H
giao điểm của AO và BE là G
Lại có \(DCO=BAO=>\frac{DCO}{2}=\frac{BAO}{2}=>FAG=HCO\)
\(FGA=CGE\)( đối đỉnh)
Xét \(\Delta AGF\)và \(\Delta CGE\):
\(AFG+FGA+FAG=GEC+CGE+ECG=180^0\)
Do \(FAG+FGA=CGE+ECG\)
\(=>CEG=AFG\)
Vì 2 góc này ở vị trí so le trong và bằng nhau
\(=>CE//AF\)
c,Ta có \(CEB=AFG\)(cm câu b)
Mà \(AFG=\frac{CAB+DBA}{2}=\frac{CAB+CDB}{2}\)(CDB = DBA Ta cm ở câu a)
\(=>CEB=\frac{CAB+CDB}{2}\left(đpcm\right)\)
a, xét ΔAOB và ΔCOD có : OA = OC (Gt)
OB = OD (gt)
^AOB = ^COD (đối đỉnh)
=> ΔAOB = ΔCAOD (c-g-c)
b, ΔAOB = ΔCAOD (Câu a)
=> ^CDO = ^OBA (định nghĩa) mà 2 góc này so le trong
=> DC // AB (Định lí)
xét ΔODA và ΔOBC có : OA = OC (gt)
OB = OD (gt)
^DOA = ^BOC (đối đỉnh)
=> ΔODA = ΔOBC (c-g-c)
=> ^ADO = ^OBC (đn) mà 2 góc này so le trong
=> AD // BC (định lí)
ΔAOB = ΔCOD (câu a)
=> ^DCO = ^OAB (định nghĩa)
CE là phân giác của ^DCO (gt) => ^ECO = ^DCO : 2 (tính chất)
AF là phân giác của ^OAB (gt) => ^OAF = ^OAB : 2 (tính chất)
=> ^ECO = ^OAF mà 2 góc này so le trong
=> CE // AF (định lí)
c, mjnh không biết làm
Cho tứ giác ABCD CÁC đoạn thẳng AB và CD cắt nhau tại O cho biết diện tích tam giác OAB OBC OCD lần lượt là 4cm 3.5cm 5.25cm tính diện tích tứ giác ABCD
Cho hình thang cân ABCD (AB//CD, AB<CD)AD cắt BC tại O
a) CMR tam giác OAB cân
b)Gọi I,J lần lượt là trung điểm của AB và CD. CMR ba điểm I,J,O thẳng hàng
a) Ta có: \(\widehat{OAB}=\widehat{ODC}\)(hai góc đồng vị, AB//CD)
\(\widehat{OBA}=\widehat{OCD}\)(hai góc đồng vị, AB//CD)
mà \(\widehat{ODC}=\widehat{OCD}\)(ABCD là hình thang cân)
nên \(\widehat{OAB}=\widehat{OBA}\)
Xét ΔOAB có \(\widehat{OAB}=\widehat{OBA}\)(cmt)
nên ΔOAB cân tại O(Định lí đảo của tam giác cân)
Đúng 1
Bình luận (0)
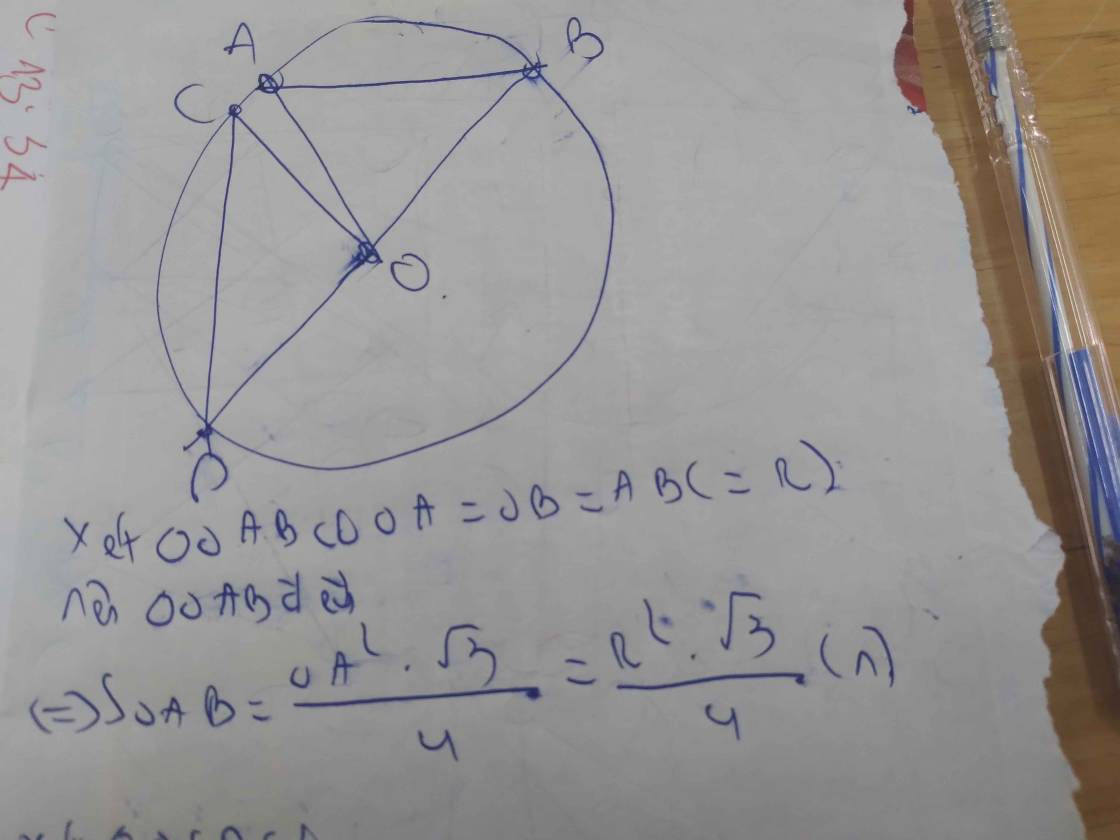
cho (o,r) và ab=r cd =r căn 3 cmr S tam giác oab = S tam giác ocd
Cho tam giác ABC trên cạnh AC lấy D sao cho CD = AB , các đương trung trực của AC và BD cắt nhau tại O . CMR
a, tam giác OAB = tam giác OCD
b, AO là tia phân giác của góc A
Cho hình thang ABCD(AB//CD). gọi o là giao điểm hai đường chéo AC và BD. Chứng minh rằng tam giác OAB đồng dạng với tam giác OCD. Chứng minh OA/AC=OB/BD. Đường thẳng a đi qua O và song song với hai đáy cắt cạnh bên AD tại M.