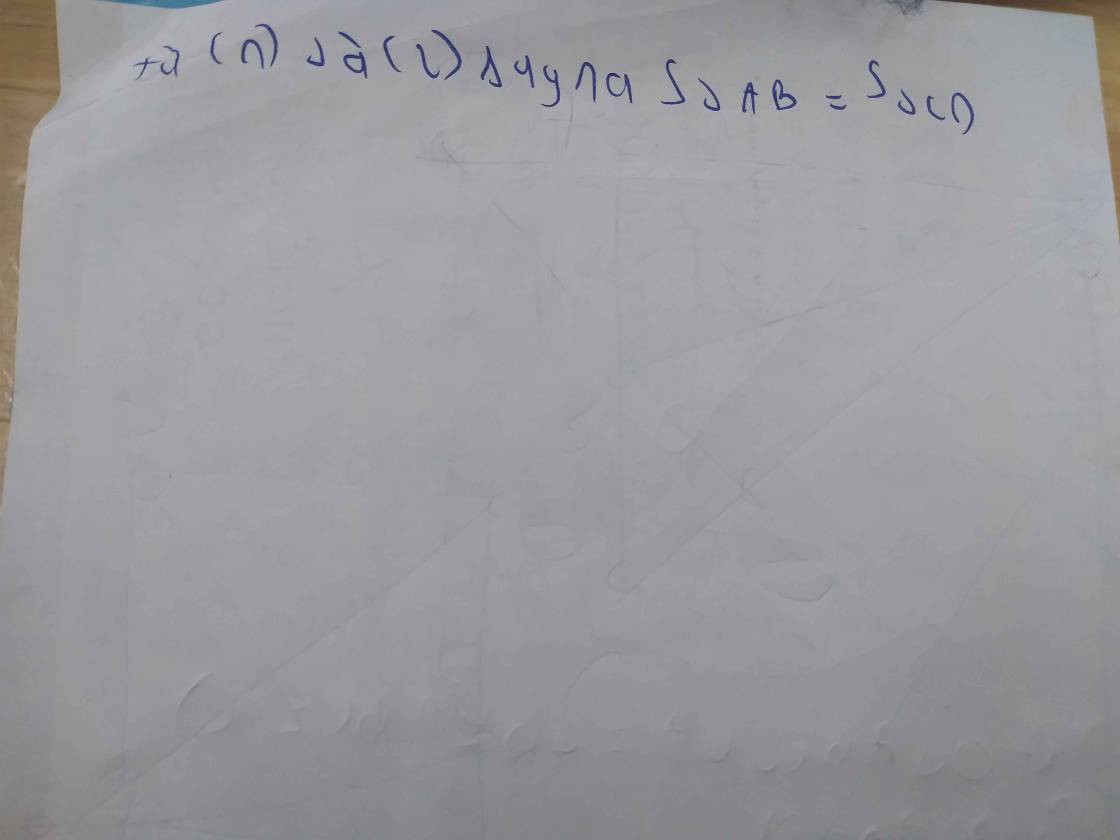Các câu hỏi tương tự
bài 1: cho hình thang vuông ABCD (vuông tại A và D ) có 2 đường chéo vuông góc với nhau tại O , AB=4cm , CD=9cm.
a) CMR : tam giác OAB đồng dạng với tam giác DAB
b) Tính độ dài AD
c) CM : tam giác OAB đồng dạng với tam giác OCD
d) Tính tỉ số diện tích của tam giác OAB và OCD
Cho tam giác ABC có 3 góc nhọn nội tiếp (O;R). AH, BK là các đường cao của tam giác ABC. Các tia AH, BK lần lượt cắt (O) tại các điểm thứ 2 là D và E.
a) CM: ABHK là tứ giác nội tiếp.
b) Cho góc ACb = 70 độ, R = 5cm. Tính S quạt OAB?
c) CM: HK // DE.
Mọi người giúp mình câu c với. :<
Cho đường tròn (O;R) với dây AB = R√2 cố định. Điểm M thuộc cung lớn AB sao cho tam giác MAB có ba góc nhọn. Các đường cao AE, BF cuar tam giác MAB cắt nhau tại H, cắt đường tròn (O) lần lượt ở P và Q.
a) CM tam giác OAB vuông cân
b) Chứng minh O, P, Q thẳng hàng
c) Gọi S là giao điểm cuaa3 PB và QA. CM SH=2R
Cho nửa đường tròn (O) đường kính AB=2R và dây cung CD. Từ A,B,O vẽ AE,BF,OI cùng vuông góc với CD.
a. Cmr I là trung điểm của CD và EF
b. AE+BF=2OI và CE=DF
c.Cho CD=R\(\sqrt{2}\). Cmr tam giác OCD vuông cân
Cho đường tròn (O;R) và đây AB = R . a)Tam giác OAB là tam giác gì ?Vì sao? b) Tính số đo các cung AB(cung n nhỏ và cung lớn).c) Kẻ đường kính AC.Tính số đo cung CAB.
Xem chi tiết
Cho AB là dây cửa đường tròn (o,r ) tính độ dài dây AB và diện tích tam giác OAB theo R biết cung AB bằng 120 độ
Xem chi tiết
Bài 3. Cho đường tròn (O; R) và dây AB của (O). Trên tia đối tia BA lấy điểm C sao cho BC R , trên nửa mặt phẳng bờ là BC có chứa điểm O dựng tam giác đều ACD. Tính tỉ số goc OCD /goc AOC
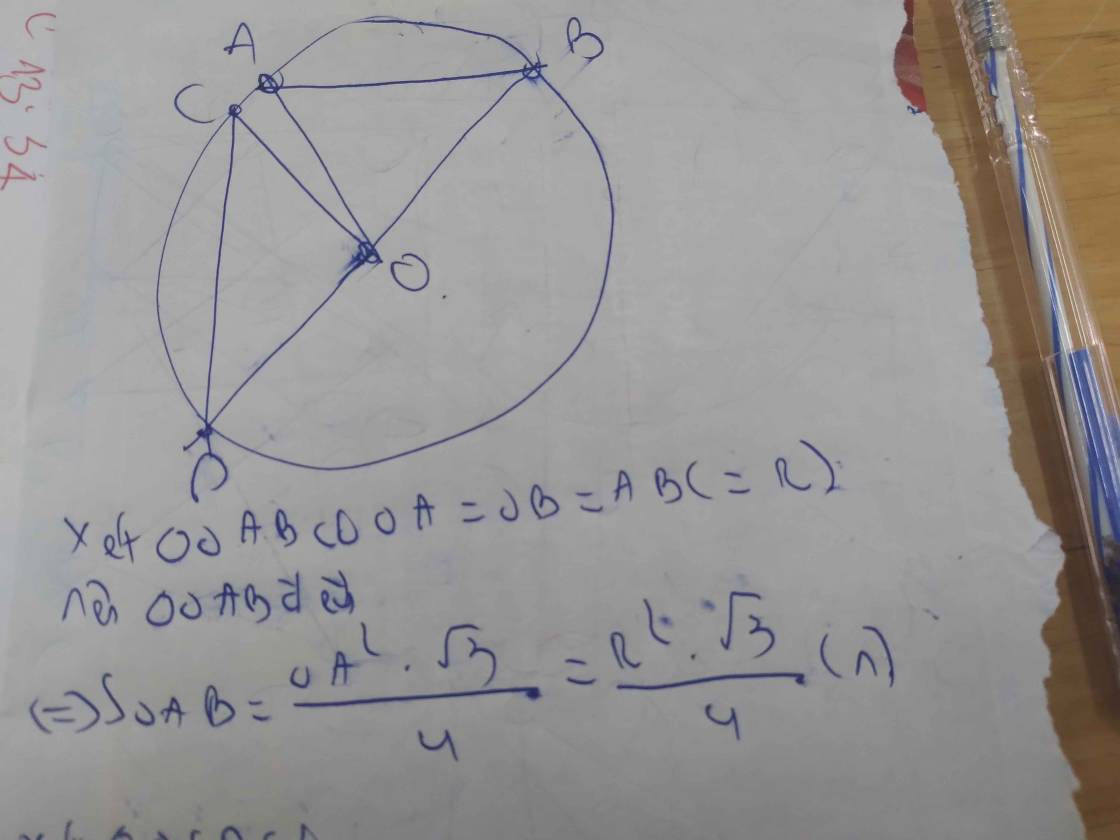
cho (O;R) và 2 dây AB ,CD trong đó CD=R căn 3
hãy xác định độ dài AB sao cho AB<CD mà S(AOB)=S(COD)
Cho AB và CD là hai đường kính vuông góc trong (O; R). Trên tia đối
CO lấy điểm S. Điểm M là giao điểm của SA và (O). Tiếp tuyến tại M của (O) cắt
CD tại E, BM cắt CD tại F.
a) Chứng minh tam giác MAO và tam giác MEF đồng dạng
b) Chứng minh E là trung điểm của SF