Cho tam giác ABC. Gọi M là trung điểm AB. Trên tia đối của tia BC lấy điểm O sao cho: BO=1/2BC. Đường OM cắt OC tại N. Chứng minh: AN=1/4AC

Những câu hỏi liên quan
Cho tam giác ABC. Gọi M là trung điểm AB. Trên tia đối của tia BC lấy điểm O sao cho: BO=1/2BC. Đường OM cắt OC tại N. Chứng minh: AN=1/4AC
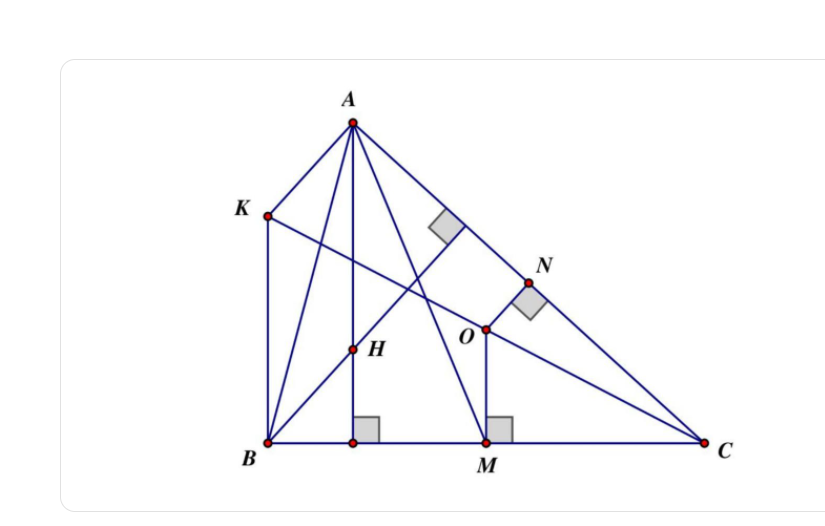
Bài 1: Cho tam giác ABC, trực tâm H. Gọi M là trung điểm của AC. Đường vuông góc với BC tại M và đường vuông góc với AC tại N cắt nhau ở O.
a) Trên tia đối tia OC, lấy điểm K sao cho OK=OC. Chứng minh rằng AHBK là hình bình hành.
b) Chứng minh OM=1/2 AH.
a, Δ KBC có KO=OC , BM=MC nên OM là đường trung bình của Δ KBC
=>=> OM//KB, OM=1/2 KB.Ta lại có OM//AH
=>=> KB//AH
Cm tương tự ta có: KA//AH
Tứ giác AHBK có: KB//AH, KA//BH nên là hình bình hành
b, Có : AHBK là hình bình hành nên KB=AH(cùng vuông góc BC)
Ta có : AM=1/2KB nên OM=1/2AH
Đúng 0
Bình luận (0)
Cho tam giác ABC vuông tại A ( AB<AC),O là trung điểm của BC . Trên tia đối OA lấy điểm K sao cho OA=OK . VẼ AH vuông góc với BC tại H . Trên tia HC lấy điểm D sao choHD=HA . Đường vuông góc với BC tại D cắt AC tại E . Chứng minh rằng : a; Tam giác ABC = tam giác CKA và OA = 1/2BC ; b, AB = AE ; c, Gọi M là trung điểm của BE . Tính góc CHM
Cho tam giác ABC cân ở A ( AB BC ) , gọi M là trung điểm của AC . Kẻ đường thẳng vuông góc với AC tại M cắt BC tại N 1. Chứng minh widehat{NAC}widehat{ACB} 2. Trên tia đối của tia AN lấy điểm P sao cho BN AP . Chứng minh AN PC 3. Gọi H , K lần lượt là trung điểm của BC và NP . Chứng minh ba đường thẳng MN , AH , CK đồng quy Giúp mk câu 3 thôi nha
Đọc tiếp
Cho tam giác ABC cân ở A ( AB > BC ) , gọi M là trung điểm của AC . Kẻ đường thẳng vuông góc với AC tại M cắt BC tại N
1. Chứng minh \(\widehat{NAC}=\widehat{ACB}\)
2. Trên tia đối của tia AN lấy điểm P sao cho BN = AP . Chứng minh AN = PC
3. Gọi H , K lần lượt là trung điểm của BC và NP . Chứng minh ba đường thẳng MN , AH , CK đồng quy
Giúp mk câu 3 thôi nha
Cho tam giác ABC. Gọi M là trung điểm của AC. Trên tia đối MB lấy điểm D sao cho MD=MB. a) Chứng minh tam giác ABM =tam giácCDM b) Chứng minh AB//CD c) Gọi N là trung điểm của BC. Kéo dài DC cắt AN tại E. Chứng minh rằng C là trung điểm của DE. d) Trên tia đối CA lấy điểm F sao cho CF=CM. Gọi O là trung điểm của EM. Chứng minh B, O, F thẳng hàng
Cho tam giác ABC có AB=1/2BC. Gọi M là trung điểm của BC, N là trung điểm của BM. Trên tia đối của tia NA lấy điểm E sao cho NA=NE. Chứng minh rằng: tam giác AEC cân.
Cho tam giác ABC có AB=1/2BC. Gọi M là trung điểm của BC, N là trung điểm của BM. Trên tia đối của tia NA lấy điểm E sao cho NA=NE. Chứng minh rằng: tam giác AEC cân.
Cho tam giác ABC có AB=1/2BC. Gọi M là trung điểm của BC, N là trung điểm của BM. Trên tia đối của tia NA lấy điểm E sao cho NA=NE. Chứng minh rằng: tam giác AEC cân.
mình lấy ở mạng nha !
Ta có: AB=12BCAB=12BC(gt)
nên BM=AB
Xét ΔENM và ΔANB có
EN=AN(gt)
ˆENM=ˆANBENM^=ANB^(hai góc đối đỉnh)
NM=NB(N là trung điểm của BM)
Do đó: ΔENM=ΔANB(c-g-c)
⇒EM=AB(hai cạnh tương ứng)
mà BM=AB(cmt)
nên EM=BM
hay EM=12BCEM=12BC(cmt)
Do đó: ΔEBC vuông tại E(Định lí)
⇒EB⊥EC
Xét ΔENB và ΔANM có
EN=AN(gt)
ˆENB=ˆANMENB^=ANM^(hai góc đối đỉnh)
BN=MN(N là trung điểm của BM)
Do đó: ΔENB=ΔANM(c-g-c)
⇒ˆBEN=ˆMANBEN^=MAN^(hai góc tương ứng)
mà ˆBENBEN^ và ˆMANMAN^ là hai góc ở vị trí so le trong
nên EB//AM(Dấu hiệu nhận biết hai đường thẳng song song)
Ta có: EB⊥EC(cmt)
EB//AM(cmt)
Do đó: EC⊥AM(Định lí 2 từ vuông góc tới song song)
Ta có: MC=MB(M là trung điểm của CB)
mà MB=2⋅MNMB=2⋅MN(N là trung điểm của MB)
nên MC=2⋅MNMC=2⋅MN
hay 12MC+MC=CN12MC+MC=CN
⇔MC=23⋅CN⇔MC=23⋅CN
Ta có: AN=EN(gt)
mà A,N,E thẳng hàng
nên N là trung điểm của AE
Xét ΔACE có
CN là đường trung tuyến ứng với cạnh AE(N là trung điểm của AE)
Đúng 0
Bình luận (2)
Cho tam giác ABC có AB=1/2BC. Gọi M là trung điểm của BC, N là trung điểm của BM. Trên tia đối của tia NA lấy điểm E sao cho NA=NE. Chứng minh rằng: tam giác AEC cân.
tham khảo
Ta có: AB=12BCAB=12BC(gt)
nên BM=AB
Xét ΔENM và ΔANB có
EN=AN(gt)
ˆENM=ˆANBENM^=ANB^(hai góc đối đỉnh)
NM=NB(N là trung điểm của BM)
Do đó: ΔENM=ΔANB(c-g-c)
⇒EM=AB(hai cạnh tương ứng)
mà BM=AB(cmt)
nên EM=BM
hay EM=12BCEM=12BC(cmt)
Do đó: ΔEBC vuông tại E(Định lí)
⇒EB⊥EC
Xét ΔENB và ΔANM có
EN=AN(gt)
ˆENB=ˆANMENB^=ANM^(hai góc đối đỉnh)
BN=MN(N là trung điểm của BM)
Do đó: ΔENB=ΔANM(c-g-c)
⇒ˆBEN=ˆMANBEN^=MAN^(hai góc tương ứng)
mà ˆBENBEN^ và ˆMANMAN^ là hai góc ở vị trí so le trong
nên EB//AM(Dấu hiệu nhận biết hai đường thẳng song song)
Ta có: EB⊥EC(cmt)
EB//AM(cmt)
Do đó: EC⊥AM(Định lí 2 từ vuông góc tới song song)
Ta có: MC=MB(M là trung điểm của CB)
mà MB=2⋅MNMB=2⋅MN(N là trung điểm của MB)
nên MC=2⋅MNMC=2⋅MN
hay 12MC+MC=CN12MC+MC=CN
⇔MC=23⋅CN⇔MC=23⋅CN
Ta có: AN=EN(gt)
mà A,N,E thẳng hàng
nên N là trung điểm của AE
Xét ΔACE có
CN là đường trung tuyến ứng với cạnh AE(N là trung điểm của AE)
Đúng 0
Bình luận (1)
Ta có: AB=12BCAB=12BC(gt)
nên BM=AB
Xét ΔENM và ΔANB có
EN=AN(gt)
ˆENM=ˆANBENM^=ANB^(hai góc đối đỉnh)
NM=NB(N là trung điểm của BM)
Do đó: ΔENM=ΔANB(c-g-c)
⇒EM=AB(hai cạnh tương ứng)
mà BM=AB(cmt)
nên EM=BM
hay EM=12BCEM=12BC(cmt)
Do đó: ΔEBC vuông tại E(Định lí)
⇒EB⊥EC
Xét ΔENB và ΔANM có
EN=AN(gt)
(hai góc đối đỉnh)
BN=MN(N là trung điểm của BM)
Do đó: ΔENB=ΔANM(c-g-c)
⇒ˆBEN=ˆMANBEN^=MAN^(hai góc tương ứng)
mà ˆBENBEN^ và ˆMANMAN^ là hai góc ở vị trí so le trong
nên EB//AM(Dấu hiệu nhận biết hai đường thẳng song song)
Ta có: EB⊥EC(cmt)
EB//AM(cmt)
Do đó: EC⊥AM(Định lí 2 từ vuông góc tới song song)
Ta có: MC=MB(M là trung điểm của CB)
mà MB=2⋅MNMB=2⋅MN(N là trung điểm của MB)
nên MC=2⋅MNMC=2⋅MN
hay 12MC+MC=CN12MC+MC=CN
⇔MC=23⋅CN⇔MC=23⋅CN
Ta có: AN=EN(gt)
mà A,N,E thẳng hàng
nên N là trung điểm của AE
Xét ΔACE có
CN là đường trung tuyến ứng với cạnh AE(N là trung điểm của AE)
Đúng 0
Bình luận (0)
Cho tam giác ABC có AB=1/2BC. Gọi M là trung điểm của BC, N là trung điểm của BM. Trên tia đối của tia NA lấy điểm E sao cho NA=NE. Chứng minh rằng: tam giác AEC cân.