5.2²+(x+3)=5² cho em xin lời giải ạ

Những câu hỏi liên quan
Tính:
a, 3/4 x 5/6= b, 2/7 : 4/9=
Cho mình xin lời giải chi tiết ạ
\(a)\dfrac{3}{4}.\dfrac{5}{6}=\dfrac{5}{8}\)
\(b)\dfrac{2}{7}:\dfrac{4}{9}=\dfrac{9}{14}\)
Đúng 0
Bình luận (0)
\(\dfrac{3}{4}x\dfrac{5}{6}=\dfrac{3x5}{4x6}=\dfrac{15}{24}=\dfrac{5}{8}\)
b) \(\dfrac{2}{7}:\dfrac{4}{9}=\dfrac{2}{7}x\dfrac{9}{4}=\dfrac{18}{28}=\dfrac{9}{14}\)
Đúng 1
Bình luận (0)
Xem thêm câu trả lời
Cho em xin lời giải bài 3 và bài 4 với ạ
Chỉ thấy bài 5 với 6:
5.
\(f'\left(x\right)+2f\left(x\right)=0\Leftrightarrow f'\left(x\right)=-2f\left(x\right)\Leftrightarrow\dfrac{f'\left(x\right)}{f\left(x\right)}=-2\)
Lấy nguyên hàm 2 vế:
\(\int\dfrac{f'\left(x\right)}{f\left(x\right)}dx=\int-2dx\Rightarrow ln\left(f\left(x\right)\right)=-2x+C\)
Thay \(x=1\Rightarrow0=-2+C\Rightarrow C=2\)
\(\Rightarrow ln\left(f\left(x\right)\right)=-2x+2\Rightarrow f\left(x\right)=e^{-2x+2}\)
\(\Rightarrow f\left(-1\right)=e^4\)
Đúng 4
Bình luận (0)
6.
\(f\left(x\right)+x.f'\left(x\right)=2x+1\)
\(\Leftrightarrow x'.f\left(x\right)+x.f'\left(x\right)=2x+1\)
\(\Leftrightarrow\left[x.f\left(x\right)\right]'=2x+1\)
Lấy nguyên hàm 2 vế:
\(\int\left[x.f\left(x\right)\right]'dx=\int\left(2x+1\right)dx\)
\(\Rightarrow x.f\left(x\right)=x^2+x+C\)
Thay \(x=1\Rightarrow1.f\left(1\right)=1+1+C\Rightarrow C=1\)
\(\Rightarrow f\left(x\right)=\dfrac{x^2+x+1}{x}\)
\(\Rightarrow f\left(2\right)=\dfrac{7}{2}\)
Đúng 1
Bình luận (0)
Ủa sao đề khác rồi:
3.
\(f'\left(x\right)=-e^x.f^2\left(x\right)\Leftrightarrow\dfrac{f'\left(x\right)}{f^2\left(x\right)}=-e^x\)
Lấy nguyên hàm 2 vế:
\(\int\dfrac{f'\left(x\right)}{f^2\left(x\right)}dx=\int-e^xdx\)
\(\Rightarrow\dfrac{1}{f\left(x\right)}=e^x+C\)
Thay \(x=0\Rightarrow2=1+C\Rightarrow C=1\)
\(\Rightarrow\dfrac{1}{f\left(x\right)}=e^x+1\Rightarrow f\left(x\right)=\dfrac{1}{e^x+1}\)
\(\Rightarrow f\left(ln2\right)=\dfrac{1}{3}\)
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
x^2017=x
cho em xin lời giải và kết quả ạ!
Nếu \(x^{2017}=x\) thì x chỉ có thể là 0 hoặc 1
Đúng 0
Bình luận (2)
x2017 = x
Vì x2017 = x nên x = 0 hoặc 1. Nhưng vì 2017 là lẻ nên x = -1 cũng được.
Vậy x = 1, -1, 0.
Đúng 0
Bình luận (0)
Cho em xin lời giải ạ !
bạn đăng tách ra để mn cùng giúp nhé
Bài 1 :
a. (d) // (d') <=> \(\left\{{}\begin{matrix}m^2-2=-1\\3\ne m+2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}m^2=1\\m\ne1\end{matrix}\right.\Leftrightarrow m=-1\)
b, Hoành độ giao điểm (d1) ; (d2) tm pt
\(2x+1=x+2\Leftrightarrow x=1\)
=> y = 3
Vậy (d1) cắt (d2) tại A(1;3)
Để 3 đường đồng quy khi (d3) đi qua A(1;3)
hay A(1;3) thuộc (d3)
<=> \(m^2+2-2m+1=3\Leftrightarrow m^2-2m=0\Leftrightarrow m=0;m=2\)
Đúng 0
Bình luận (1)
\(\sqrt{x+2\sqrt{2x-4}}+\sqrt{x-2\sqrt{2x-4}}=2\sqrt{2}\)giải phương trình ( cho em xin lời giải chi tiết ạ )
\(\sqrt{x+2\sqrt{2x-4}}+\sqrt{x-2\sqrt{2x-4}}=2\sqrt{2}\)
\(\Leftrightarrow\sqrt{x+2\sqrt{2\left(x-2\right)}}+\sqrt{x-2\sqrt{2\left(x-2\right)}}=2\sqrt{2}\)
\(\Leftrightarrow2x+2\sqrt{\left[x+2\sqrt{2\left(x-2\right)}\text{ }\right]\left[x-2\sqrt{2\left(x-2\right)}\text{ }\right]}=8\)
\(\Leftrightarrow2\sqrt{\left[x+2\sqrt{2\left(x-2\right)}\text{ }\right]\left[x-2\sqrt{2\left(x-2\right)}\text{ }\right]}=8-2x\)
\(\Leftrightarrow4\left[x+2\sqrt{2\left(x-2\right)}\text{ }\right]\left[x-2\sqrt{2\left(x-2\right)}\text{ }\right]=64-32x+4x^2\)
\(\Leftrightarrow4x^2-32x+64=64-32x+4x^2+\)
\(\Leftrightarrow64=64\) (Đúng)
⇒ Phương trình có vô số nghiệm.
Vậy \(S=\mathbb R\).
Đúng 1
Bình luận (6)
\(\sqrt{x+2\sqrt{2x-4}}+\sqrt{x-2\sqrt{2x-4}}=2\sqrt{2}\)
ĐK: \(x\ge2\), PT tương đương với:
\(x+2\sqrt{2x-4}+2\sqrt{\left(x+2\sqrt{2x-4}\right)\left(x-2\sqrt{2x-4}\right)}+x-2\sqrt{2x-4}=8\)
\(\Leftrightarrow2x+2\sqrt{x^2-4\left(2x-4\right)}=8\)
\(\Leftrightarrow2x+2\sqrt{x^2-8x+16}=8\\ \Leftrightarrow x+\left|x-4\right|=8\)
Với x < 4 => \(x+4-x=8\)
\(\Leftrightarrow4=8\) (loại)
Với \(x\ge4\) => \(x+x-4=8\)
\(\Leftrightarrow x=6\) (thỏa mãn)
Đúng 1
Bình luận (6)
Mn cho em xin lời giải bài này ạ..... Em cảm ơn mn nhiều ạ

\(y'=-3mx^2+2x-3\)
Hàm nghịch biến trên khoảng đã cho khi với mọi \(x\in\left(-3;0\right)\) ta có:
\(-3mx^2+2x-3\le0\)
\(\Leftrightarrow2x-3\le3mx^2\)
\(\Leftrightarrow\dfrac{2x-3}{3x^2}\le m\)
\(\Rightarrow m\ge\max\limits_{\left(-3;0\right)}\left(\dfrac{2x-3}{3x^2}\right)\)
Xét hàm \(f\left(x\right)=\dfrac{2x-3}{3x^2}\Rightarrow f'\left(x\right)=\dfrac{2\left(3-x\right)}{3x^3}< 0;\forall x\in\left(-3;0\right)\)
\(\Rightarrow f\left(x\right)>f\left(-3\right)=-\dfrac{1}{3}\)
\(\Rightarrow m\ge-\dfrac{1}{3}\)
Đúng 1
Bình luận (0)
Cho em xin lời giải bài này ạ!!! Em cảm ơn ![]()
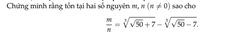
Đặt \(x=\sqrt[3]{\sqrt[]{50}+7}-\sqrt[3]{\sqrt[]{50}-7}\)
\(x^3=14-3\sqrt[3]{\left(\sqrt[]{50}+7\right)\left(\sqrt[]{50}-7\right)}\left(\sqrt[3]{\sqrt[]{50}+7}-\sqrt[3]{\sqrt[]{50}-7}\right)\)
\(x^3=14-3x\)
\(x^3+3x-14=0\)
\(\left(x-2\right)\left(x^2+2x+7\right)=0\)
\(x=2\)
\(\Rightarrow\dfrac{m}{n}=2\)
\(\Rightarrow\) Hiển nhiên tồn tại vô số m, n nguyên thỏa mãn đẳng thức trên
Đúng 0
Bình luận (0)
Mọi người cho em xin lời giải ạ
Đọc tiếp
Mọi người cho em xin lời giải ạ
Cho em xin lời giải chi tiết ạ

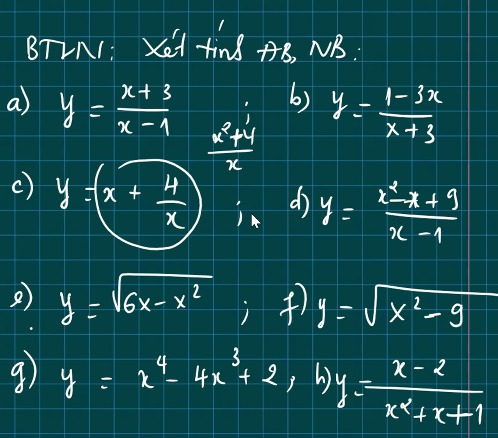 Cho em xin lời giải chi tiết với ạ
Cho em xin lời giải chi tiết với ạ
f.
TXĐ: \(x\in(-\infty;-3]\cup[3;+\infty)\)
\(y'=\dfrac{2x}{2\sqrt{x^2-9}}=\dfrac{x}{\sqrt{x^2-9}}\)
Dấu của y':

Hàm đồng biến trên \([3;+\infty)\) và nghịch biến trên \((-\infty;-3]\)
g.
\(y'=4x^3-12x^2=4x^2\left(x-3\right)=0\Rightarrow x=3\) (khi tìm khoảng đơn điệu hay cực trị của hàm số thì chỉ cần quan tâm nghiệm bội lẻ, không cần quan tâm nghiệm bội chẵn)
Dấu của y':
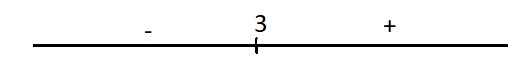
Hàm đồng biến trên \(\left(3;+\infty\right)\) và nghịch biến trên \(\left(-\infty;3\right)\)
h.
\(y'=\dfrac{x^2+x+1-\left(x-2\right)\left(2x+1\right)}{\left(x^2+x+1\right)^2}=\dfrac{-x^2+4x+3}{\left(x^2+x+1\right)^2}\)
\(y'=0\Leftrightarrow-x^2+4x+3=0\Rightarrow\left[{}\begin{matrix}x=2-\sqrt{7}\\x=2+\sqrt{7}\end{matrix}\right.\)
Dấu của y':
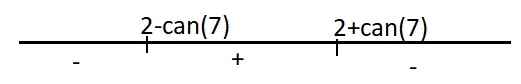
Hàm đồng biến trên \(\left(2-\sqrt{7};2+\sqrt{7}\right)\)
Hàm nghịch biến trên các khoảng \(\left(-\infty;2-\sqrt{7}\right)\) và \(\left(2+\sqrt{7};+\infty\right)\)
Đúng 0
Bình luận (0)


























