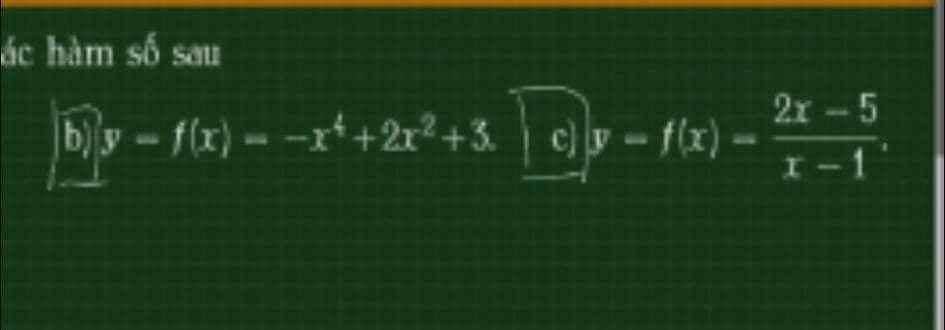f.
TXĐ: \(x\in(-\infty;-3]\cup[3;+\infty)\)
\(y'=\dfrac{2x}{2\sqrt{x^2-9}}=\dfrac{x}{\sqrt{x^2-9}}\)
Dấu của y':

Hàm đồng biến trên \([3;+\infty)\) và nghịch biến trên \((-\infty;-3]\)
g.
\(y'=4x^3-12x^2=4x^2\left(x-3\right)=0\Rightarrow x=3\) (khi tìm khoảng đơn điệu hay cực trị của hàm số thì chỉ cần quan tâm nghiệm bội lẻ, không cần quan tâm nghiệm bội chẵn)
Dấu của y':
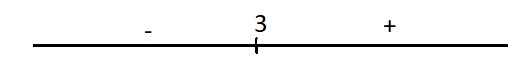
Hàm đồng biến trên \(\left(3;+\infty\right)\) và nghịch biến trên \(\left(-\infty;3\right)\)
h.
\(y'=\dfrac{x^2+x+1-\left(x-2\right)\left(2x+1\right)}{\left(x^2+x+1\right)^2}=\dfrac{-x^2+4x+3}{\left(x^2+x+1\right)^2}\)
\(y'=0\Leftrightarrow-x^2+4x+3=0\Rightarrow\left[{}\begin{matrix}x=2-\sqrt{7}\\x=2+\sqrt{7}\end{matrix}\right.\)
Dấu của y':
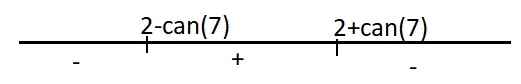
Hàm đồng biến trên \(\left(2-\sqrt{7};2+\sqrt{7}\right)\)
Hàm nghịch biến trên các khoảng \(\left(-\infty;2-\sqrt{7}\right)\) và \(\left(2+\sqrt{7};+\infty\right)\)

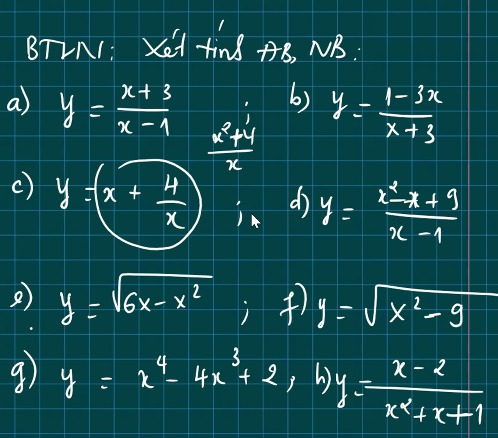 Cho em xin lời giải chi tiết với ạ
Cho em xin lời giải chi tiết với ạ