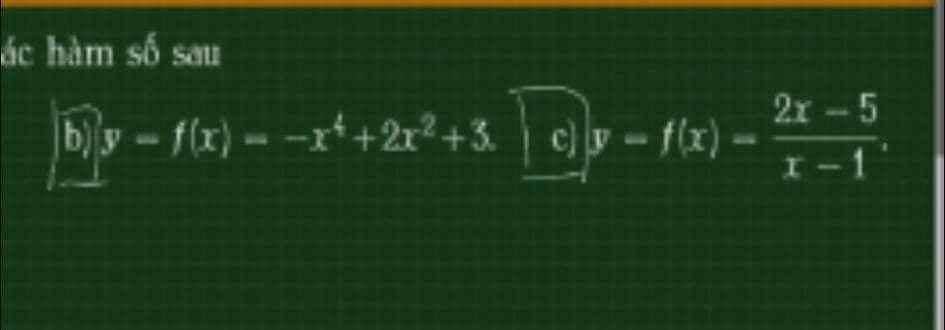cái hồi nãy thiếu câu hỏi em bổ sung ở dưới này ạ
em cảm ơn mn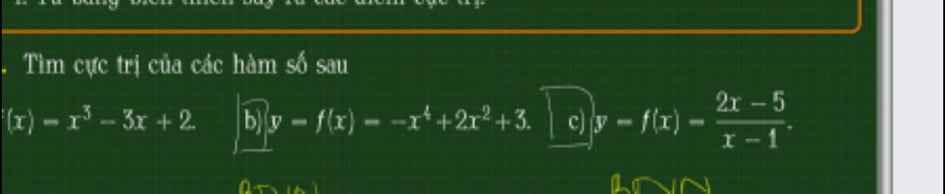
5.
TXĐ: \(D=\left(-\infty;-1\right)\cup\left(-1;+\infty\right)\)
\(y'=\dfrac{2}{\left(x+1\right)^2}>0\) ; \(\forall x\in D\)
\(\Rightarrow\) Hàm đồng biến trên mỗi khoảng xác định
Hay hàm đồng biến trên \(\left(-\infty;-1\right)\) và \(\left(-1;+\infty\right)\)
6.
\(y=4x^3-4x=0\Rightarrow\left[{}\begin{matrix}x=0\\x=-1\\x=1\end{matrix}\right.\)
Dấu của y' trên trục số:
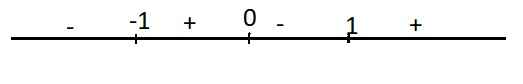
Từ đó ta thấy:
Hàm đồng biến trên các khoảng \(\left(-1;0\right)\) và \(\left(1;+\infty\right)\)
Hàm nghịch biến trên các khoảng \(\left(-\infty;-1\right)\) và \(\left(1;+\infty\right)\)
Tìm cực trị
a.
\(f'\left(x\right)=3x^2-3=0\Rightarrow x=\pm1\)
\(f''\left(x\right)=6x\)
\(f''\left(-1\right)=-6< 0\)
\(f''\left(1\right)=6>0\)
\(\Rightarrow x=-1\) là điểm cực đại và \(x=1\) là điểm cực tiểu
b.
\(f'\left(x\right)=-4x^3+4x=0\Rightarrow\left[{}\begin{matrix}x=0\\x=-1\\x=1\end{matrix}\right.\)
\(f''\left(x\right)=-12x^2+4\)
\(f''\left(0\right)=4>0\) ; \(f''\left(-1\right)=-8< 0\) ; \(f''\left(1\right)=-8< 0\)
\(\Rightarrow x=0\) là điểm cực tiểu và \(x=\pm1\) là 2 điểm cực đại
c.
\(f'\left(x\right)=\dfrac{3}{\left(x-1\right)^2}\ne0\) với mọi x thuộc miền xác định
Hàm không có cực trị