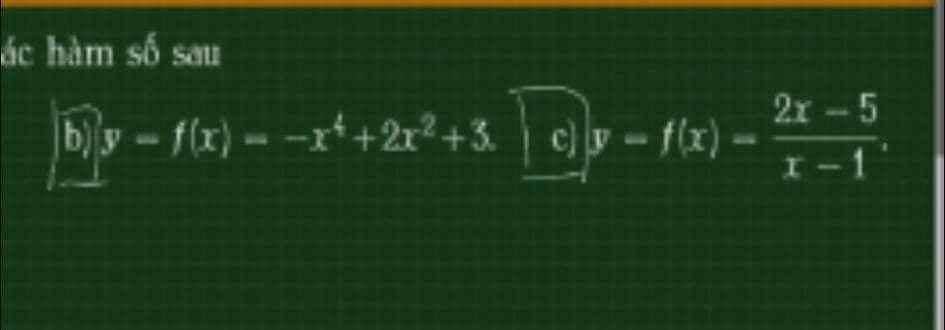4a.
\(y'=\dfrac{1}{cos^2x}+cosx-2=\dfrac{cos^3x-2cos^2x+1}{cos^2x}=\dfrac{\left(1-cosx\right)\left(1+cosx\left(1-cosx\right)\right)}{cos^2x}>0\) ; \(\forall x\in\left(0;\dfrac{\pi}{2}\right)\)
\(\Rightarrow\) Hàm đồng biến trên \(\left(0;\dfrac{\pi}{2}\right)\)
4b.
\(y'=-sinx-1\le0\) ; \(\forall x\in\left(0;2\pi\right)\)
\(\Rightarrow\) Hàm nghịch biến trên \(\left(0;2\pi\right)\)
c.
\(y'=-sinx-\dfrac{1}{sin^2x}+2=\dfrac{-sin^3x+2sin^2x-1}{sin^2x}=\dfrac{\left(sinx-1\right)\left(1-sin^2x+sinx\right)}{sin^2x}\)
\(=\dfrac{\left(sinx-1\right)\left(cos^2x+sinx\right)}{sin^2x}< 0\) ; \(\forall x\in\left(0;\dfrac{\pi}{2}\right)\)
\(\Rightarrow\) Hàm nghịch biến trên \(\left(0;\dfrac{\pi}{2}\right)\)
4d.
\(y=cosx+sinx.cosx=cosx+\dfrac{1}{2}sin2x\)
\(y'=-sinx+cos2x=-sinx+1-2sin^2x\)
\(y'=0\Leftrightarrow\left[{}\begin{matrix}sinx=-1\\sinx=\dfrac{1}{2}\end{matrix}\right.\)
\(\Rightarrow x=\left\{\dfrac{\pi}{6};\dfrac{5\pi}{6};\dfrac{3\pi}{2}\right\}\)
Bảng biến thiên
Từ BBt ta thấy hàm đồng biến trên các khoảng \(\left(0;\dfrac{\pi}{6}\right)\) và \(\left(\dfrac{5\pi}{6};2\pi\right)\)
Hàm nghịch biến trên \(\left(\dfrac{\pi}{6};\dfrac{5\pi}{6}\right)\)
5a.
\(y'=x^2-4x+m\)
Hàm đồng biến trên TXĐ khi và chỉ khi \(y'\ge0\) ; \(\forall x\in R\)
\(\Leftrightarrow\left\{{}\begin{matrix}a=1>0\\\Delta'=4-m\le0\end{matrix}\right.\)
\(\Leftrightarrow m\ge4\)