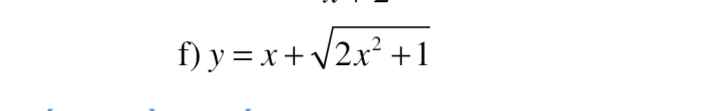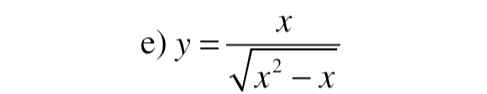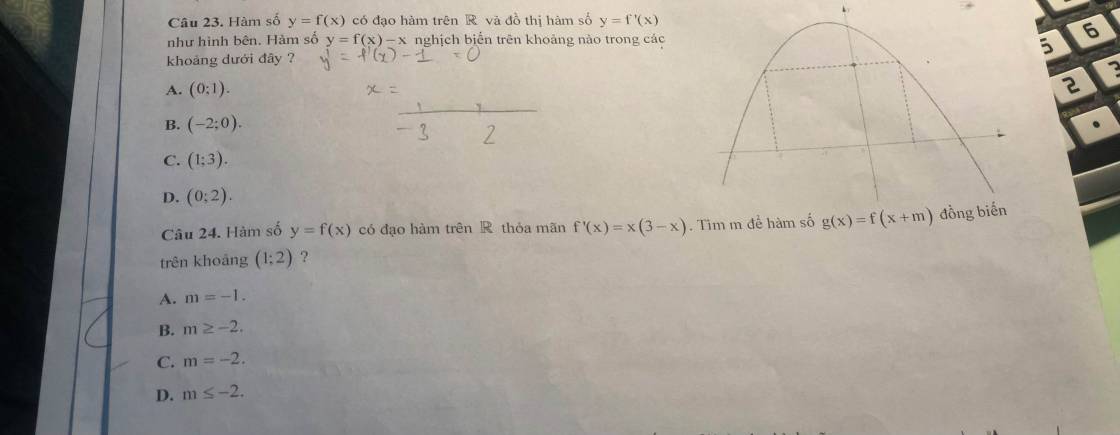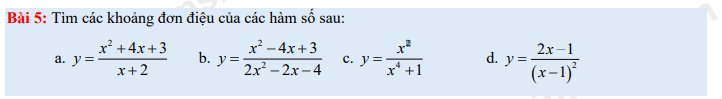\(y'=3f'\left(x+2\right)-3\left(x^2-1\right)\)
\(y'>0\Rightarrow f'\left(x+2\right)>x^2-1\)
Đặt \(x+2=t\Rightarrow f'\left(t\right)>t^2-4t+3\)
Nhận thấy \(\left\{{}\begin{matrix}f'\left(t\right)=0\\t^2-4t+3=0\end{matrix}\right.\) đều có 2 nghiệm \(\left[{}\begin{matrix}t=1\\t=3\end{matrix}\right.\) nên ta có phác thảo 2 đồ thị:
(Và lưu ý hàm \(t^2-4t+3\) đồng biến khi t>2, nghịch biến khi t<2)
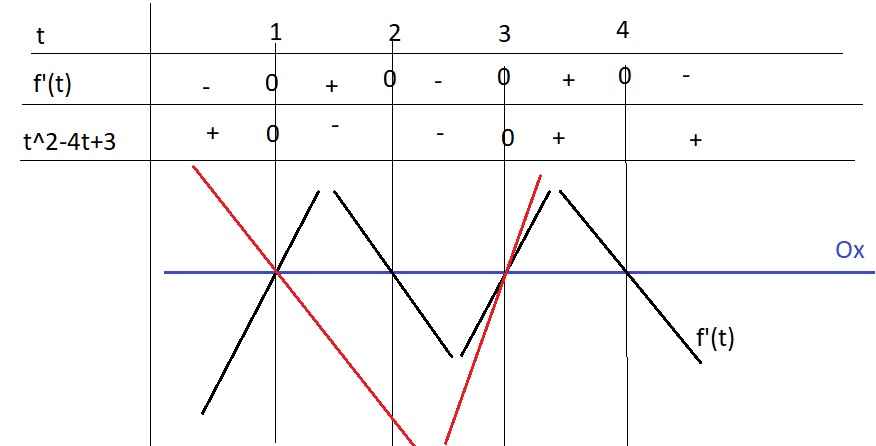
Từ đây ta thấy \(f'\left(t\right)>t^2-4t+3\) khi \(t\in\left(1;3\right)\Rightarrow x+2\in\left(1;3\right)\Rightarrow x\in\left(-1;1\right)\) và các tập con của nó
\(\Rightarrow\) B
Đúng 0
Bình luận (0)
