Cho hs y=x+m(d).Xác định m để (d) tạo vs hai trục tọa độ một tam giác có diện tích bằng 12

Những câu hỏi liên quan
Xác định m để đường thẳng y = x + m + 1 tạo với các trục tọa độ một tam giác có diện tích bằng 8 (đvdt)
Gọi giao của đường thẳng và trục Ox là A => A(m+1;0)
=> OA = | m+1 |
Gọi giao của đường thẳng với trục Oy là B => B(0 ; m+1)
=> OB=|m+1|
Theo đề bài ta có S ABC =8
<=> 1/2 x OA x OB= 8
<=> 1/2 x |m+1| x |m+1| = 8
từ đó giải ra m=3
#HT#
Trả lời : m = 3
#HT#
Cho hàm số y =(m – 3)x + 2 có đồ thị là (d)
c) Tìm m để (d) cắt hai trục tọa độ tạo thành một tam giác có diện tích bằng 4.
c) y = (m – 3)x + 2 (m ≠ 3)
Gọi A, B lần lượt là giao điểm của (d) và trục Ox, Oy và tam giác tạo thành là tam giác AOB vuông tại O
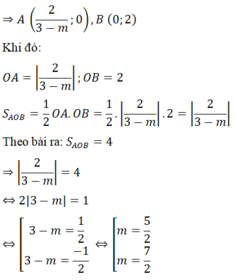
Đúng 0
Bình luận (0)
Tìm m để đường thẳng d: y=(m2 +2)x+1 tạo với hai trục tọa độ một tam giác có diện tích bằng \(\dfrac{1}{8}\)
Gọi A và B lần lượt là giao điểm của d với Ox và Oy
\(\Rightarrow A\left(-\dfrac{1}{m^2+2};0\right)\) ; \(B\left(0;1\right)\) \(\Rightarrow OA=\dfrac{1}{m^2+2}\) ; \(OB=1\)
\(S_{OAB}=\dfrac{1}{2}OA.OB=\dfrac{1}{8}\Leftrightarrow OA.OB=\dfrac{1}{4}\)
\(\Leftrightarrow\dfrac{1}{m^2+2}=\dfrac{1}{4}\Rightarrow m^2=2\Rightarrow m=\pm\sqrt{2}\)
Đúng 0
Bình luận (0)
Cho (d): y=mx-2
xác định giá trị của m sao cho (d) cắt 2 trục tọa độ tạo thành tam giác có diện tích bằng 1
(d) cắt hai trục tọa độ tao thành tam giác ⇔ m \(\ne\)0
Gọi (d) cắt Ox, Oy lần lượt tại A, B
\(\Rightarrow\)A( \(\frac{2}{m}\); 0)\(\Rightarrow\)OA= trị tuyệt đối của \(\frac{2}{m}\)
=> B(0; -2) => OB= trị tuyệt đối của -2
xét tam giác cân AOB có AOB= 90 độ
OA=OB
=> trị tuyệt đố của \(\frac{2}{m}\)= trị tuyệt đối của -2
TH1: \(\frac{2}{m}\)=2
<=> 2=2m
<=> m=1 (t/m)
TH2 \(\frac{2}{m}\)= -2
<=> 2=-2m
<=>m=-1(t/m)
Vậy để d cắt 2 trục tọa độ tạo thành tam giác cân thì m=1 hoặc m=-1
Đúng 0
Bình luận (0)
Bài 8. Cho đường thẳng có phương trình y = (m - 1)x + 2m (m khác 1). Tìm m để đường thẳng cắt hai trục tọa độ và tạo với hai trục tọa độ một tam giác có diện tích bằng 1 (đơn vị diện tích).
Bài 1 : Xác định phương trình : d:y=ax+b biết :
d song song với d1 : y = x-3 và đi qua 1 điểm trên trục hoành có hoành độ bằng 5
Bài 2 : Tìm m để : \(d:y=\left(2m^2+1\right)x+2\) tạo với hai trục tọa độ tam giác có diện tích bằng 2/19
help me
Bài 1:
Vì (d)//(d1) nên a=1 và \(b\ne-3\)
hay (d):y=x+b
Vì (d) đi qua một điểm trên trục hoành có hoành độ bằng 5 nên
Thay x=5 và y=0 vào hàm số y=x+b, ta được
\(b+5=0\)
hay b=-5
Vậy: (d): y=x-5
Đúng 1
Bình luận (0)
Cho đường thẳng
d
:
y
2
m
+
1
x
−
1
. Tìm m để đường thẳng d cắt hai trục tọa độ tạo thành tam giác có diện tích bằng
1
2
A.
m
0
B.
m
1
C.
m...
Đọc tiếp
Cho đường thẳng d : y = 2 m + 1 x − 1 . Tìm m để đường thẳng d cắt hai trục tọa độ tạo thành tam giác có diện tích bằng 1 2
A. m = 0
B. m = 1
C. m = − 1
D. Cả A và C đều đúng
d ∩ O y = B ⇒ x B = 0 ⇒ y B = − 1 ⇒ B 0 ; − 1 ⇒ O B = − 1 = 1 d ∩ O x = A ⇒ y A = 0 2 m + 1 x – 1 = 0 ⇔ x A = 1 2 m + 1 m ≠ − 1 2
⇒ A 1 2 m + 1 ; 0 ⇒ O A = 1 2 m + 1
S Δ A O B = 1 2 O A . O B = 1 2 .1. 1 2 m + 1 = 1 2 ⇔ | 2 m + 1 | = 1 ⇔ m = 0 m = − 1
Đáp án cần chọn là: D
Đúng 0
Bình luận (0)
Cho hàm số bậc nhất: y (m+2) .x+ 3 có đồ thị là đường thẳng (d)a) Tìm m biết (d) song song với đường thẳng ( d/): y -2x+4. b) Tìm m để (d) tạo với hai trục tọa độ một tam giác có diện tích bằng 6 đvdt.
Đọc tiếp
Cho hàm số bậc nhất: y= (m+2) .x+ 3 có đồ thị là đường thẳng (d)
a) Tìm m biết (d) song song với đường thẳng ( d/): y = -2x+4.
b) Tìm m để (d) tạo với hai trục tọa độ một tam giác có diện tích bằng 6 đvdt.
a: Để (d)//(d') thì m+2=-2
hay m=-4
Đúng 0
Bình luận (0)
a) Viết pt đường thẳng y =ax +b biết đồ thị của nó đi qua điểm S (2;3) và cắt trục tọa độ tại hai điểm M,N sao cho tam giác OMN có diện tích bằng 2
b) Tìm m để đồ thị hàm số y=m2x +m +1 tạo vs các trục tọa độ một tam giác cân
Bài 7: Cho hàm số y = (m - 2)x + m + 3 với m ≠ 2
a) Xác định giá trị của m để hàm số đồng biến, nghịch biến
b) Tìm m để đồ thị hàm số cắt hai trục tọa độ tạo thành tam giác có diện tích bằng 1.
Giúp mk nha
\(a,\) Đồng biến \(\Leftrightarrow m-2>0\Leftrightarrow m>2\)
Nghịch biến \(\Leftrightarrow m-2< 0\Leftrightarrow m< 2\)
\(b,\) PT giao Ox: \(y=0\Leftrightarrow\left(m-2\right)x=-\left(m+3\right)\Leftrightarrow x=\dfrac{m+3}{2-m}\Leftrightarrow A\left(\dfrac{m+3}{2-m};0\right)\Leftrightarrow OA=\left|\dfrac{m+3}{2-m}\right|\)
PT giao Oy: \(x=0\Leftrightarrow y=m+3\Leftrightarrow B\left(0;m+3\right)\Leftrightarrow OB=\left|m+3\right|\)
Theo đề: \(S_{OAB}=\dfrac{1}{2}OA\cdot OB=1\)
\(\Leftrightarrow\left|\dfrac{m+3}{2-m}\right|\left|m+3\right|=2\\ \Leftrightarrow\dfrac{\left(m+3\right)^2}{\left|2-m\right|}=2\\ \Leftrightarrow2\left|2-m\right|=\left(m+3\right)^2\\ \Leftrightarrow\left[{}\begin{matrix}2\left(2-m\right)=\left(m+3\right)^2\left(m\le2\right)\\2\left(m-2\right)=\left(m+3\right)^2\left(m>2\right)\end{matrix}\right.\\ \Leftrightarrow\left[{}\begin{matrix}m^2+8m+5=0\left(m\le2\right)\\m^2+4m+13=0\left(vô.n_0\right)\end{matrix}\right.\\ \Leftrightarrow\left[{}\begin{matrix}m=-4+\sqrt{11}\left(n\right)\\m=-4-\sqrt{11}\left(n\right)\end{matrix}\right.\)
Vậy ...
Đúng 0
Bình luận (0)



















