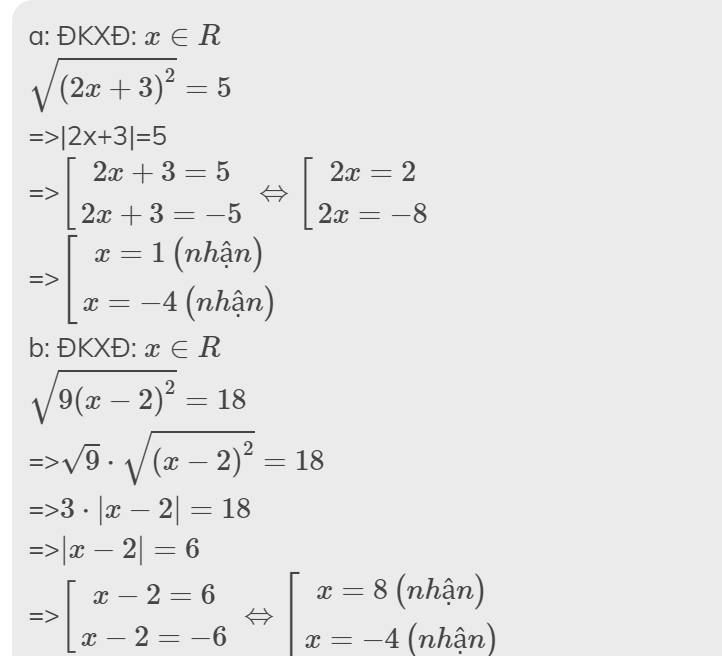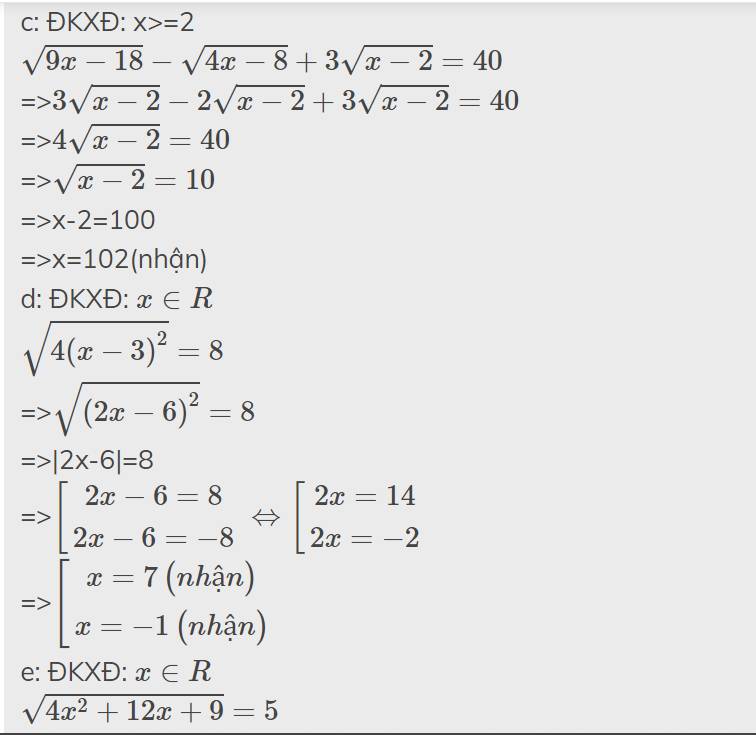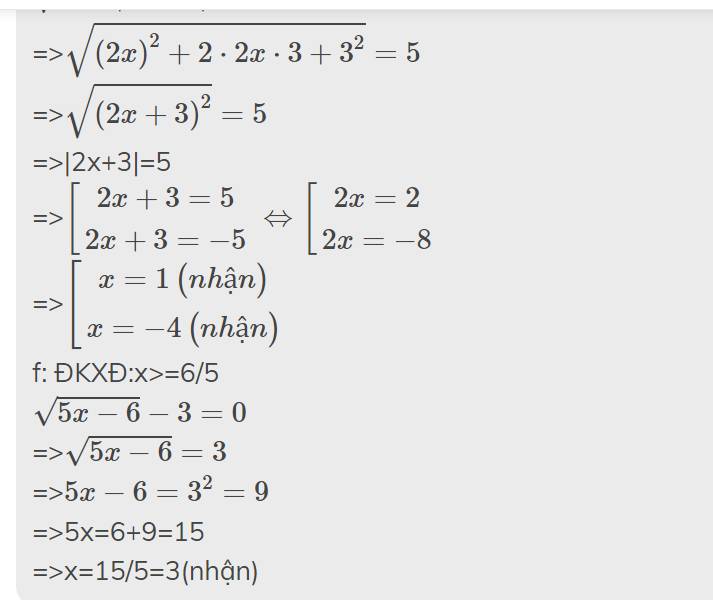Do có quá ít câu hỏi nên bạn nào trả lời được, mình sẽ xóa khỏi mục "Câu hỏi hay" nhé!

Tham khảo:

1) Giải phương trình : \(11\sqrt{5-x}+8\sqrt{2x-1}=24+3\sqrt{\left(5-x\right)\left(2x-1\right)}\) - Hoc24

\(\sqrt{x+3}+2\sqrt{x}=2+\sqrt{x\left(x+3\right)}\left(đk:x\ge0\right)\)

\(\Leftrightarrow x+3+4x+4\sqrt{x\left(x+3\right)}=4+x\left(x+3\right)+4\sqrt{x\left(x+3\right)}\)

\(\Leftrightarrow5x+3=4+x^2+3x\)

\(\Leftrightarrow x^2-2x+1=0\)

\(\Leftrightarrow\left(x-1\right)^2=0\)

\(\Leftrightarrow x-1=0\)

\(\Leftrightarrow x=1\left(tm\right)\)

Sửa lại câu c) đặt \(\sqrt{x}+1=\)t \(\Rightarrow\left[2\left(t+\dfrac{1}{2}\right)\right]\left(t-3\right)\)=7⇒\(\left\{{}\begin{matrix}t=3\\t=-\dfrac{1}{2}\end{matrix}\right.\)

\(\Rightarrow\left\{{}\begin{matrix}x=4\\x=\dfrac{9}{4}\end{matrix}\right.\)

a) \(\left(\sqrt{4-3x}\right)^2=8^2\)\(\Leftrightarrow4-3x=64\Rightarrow x=-20\)

b) \(\sqrt{4x-8}+1=12\sqrt{\dfrac{x-2}{9}}\Leftrightarrow2\sqrt{x-2}+1\)\(=\left(12\sqrt{\left(x-2\right).\dfrac{1}{9}}\right)\)

\(\Leftrightarrow2t+1=12.\dfrac{1}{3}t\) (Đặt t = \(\sqrt{x-2}\))

\(\Rightarrow t=\dfrac{1}{2}\) \(\Rightarrow\sqrt{x-2}=\dfrac{1}{2}\)\(\Rightarrow x=\dfrac{9}{4}\)

c) pt\(\Leftrightarrow\left\{{}\begin{matrix}2\sqrt{x}+1=7\\\sqrt{x}-2=7\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}\sqrt{x}=3\\\sqrt{x}=2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=9\\x=4\end{matrix}\right.\)

a) Ta có: \(\sqrt{4-3x}=8\)

\(\Leftrightarrow4-3x=64\)

\(\Leftrightarrow3x=4-64=-60\)

hay x=-20

b) Ta có: \(\sqrt{4x-8}-12\cdot\sqrt{\dfrac{x-2}{9}}=-1\)

\(\Leftrightarrow2\cdot\sqrt{x-2}-12\cdot\dfrac{\sqrt{x-2}}{3}=-1\)

\(\Leftrightarrow-2\cdot\sqrt{x-2}=-1\)

\(\Leftrightarrow\sqrt{x-2}=\dfrac{1}{2}\)

\(\Leftrightarrow x-2=\dfrac{1}{4}\)

hay \(x=\dfrac{9}{4}\)

a: Ta có: \(\sqrt{4-3x}=8\)

\(\Leftrightarrow4-3x=64\)

\(\Leftrightarrow3x=-60\)

hay x=-20

b: ta có: \(\sqrt{4x-8}-12\sqrt{\dfrac{x-2}{9}}=-1\)

\(\Leftrightarrow2\sqrt{x-2}-12\cdot\dfrac{\sqrt{x-2}}{3}=-1\)

\(\Leftrightarrow x-2=\dfrac{1}{4}\)

hay \(x=\dfrac{9}{4}\)

\(\left\{{}\begin{matrix}8>0\left(luondung\right)\\4-3x=64\end{matrix}\right.\) \(\Leftrightarrow x=-20\left(ktm\right)\)

Đặt \(\sqrt{x^2+9}=t>0\) ta được:

\(t^2+8x=\left(x+8\right)t\Leftrightarrow t^2-\left(x+8\right)t+8x=0\)

\(\Leftrightarrow t^2-tx-8t+8x=0\)

\(\Leftrightarrow t\left(t-x\right)-8\left(t-x\right)=0\)

\(\Leftrightarrow\left(t-x\right)\left(t-8\right)=0\)

\(\Rightarrow\left[{}\begin{matrix}\sqrt{x^2+9}=x\left(x\ge0\right)\\\sqrt{x^2+9}=8\end{matrix}\right.\)

\(\Rightarrow\left[{}\begin{matrix}x^2+9=x^2\left(vn\right)\\x^2=55\end{matrix}\right.\)

\(\Rightarrow x=\pm\sqrt{55}\)

ĐKXĐ: \(0\le x\le5\).

Đặt \(\left\{{}\begin{matrix}\sqrt{x}=a\\\sqrt{5-x}=b\end{matrix}\right.\left(a,b\ge0\right)\).

PT đã cho tương đương với: \(\left(8-ab\right)\left(a-b\right)=2\left(a-b\right)\)

\(\Leftrightarrow\left[{}\begin{matrix}a=b\\ab=6\end{matrix}\right.\).

+) \(a=b\Leftrightarrow\sqrt{x}=\sqrt{5-x}\Leftrightarrow x=2,5\left(TMĐK\right)\).

+) \(ab=6\Leftrightarrow\sqrt{x\left(5-x\right)}=6\Leftrightarrow x^2-5x+6=0\Leftrightarrow\left[{}\begin{matrix}x=2\left(TMĐK\right)\\x=3\left(TMĐK\right)\end{matrix}\right.\).

Vậy...

ĐK: \(0\le x\le5\)

Đặt \(\left\{{}\begin{matrix}\sqrt{x}=a\\\sqrt{5-x}=b\end{matrix}\right.\left(a,b\ge0\right)\)

\(pt\Leftrightarrow\left(8-ab\right)\left(a-b\right)=2\left(a^2-b^2\right)\)

\(\Leftrightarrow\left(a-b\right)\left(8-ab-2a-2b\right)=0\)

\(\Leftrightarrow\left[{}\begin{matrix}a-b=0\\ab+2a+2b=8\end{matrix}\right.\)

TH1: \(a=b\Leftrightarrow\sqrt{x}=\sqrt{5-x}\Leftrightarrow x=\dfrac{5}{2}\left(tm\right)\)

TH2: \(ab+2a+2b=8\)

\(\Leftrightarrow\sqrt{5x-x^2}+2\sqrt{5-x}+2\sqrt{x}=8\)

\(\Leftrightarrow\left(\sqrt{5-x}+\sqrt{x}-3\right)\left(\sqrt{5-x}+\sqrt{x}+7\right)=0\)

\(\Leftrightarrow\left[{}\begin{matrix}\sqrt{5-x}+\sqrt{x}=-7\left(l\right)\\\sqrt{5-x}+\sqrt{x}=3\end{matrix}\right.\)

\(\sqrt{5-x}+\sqrt{x}=3\)

\(\Leftrightarrow5+2\sqrt{5x-x^2}=9\)

\(\Leftrightarrow\left[{}\begin{matrix}x=4\left(tm\right)\\x=1\left(tm\right)\end{matrix}\right.\)

Vậy ...