Câu 19 ạ

Những câu hỏi liên quan
Câu 14 đến câu 19 ạ
11 milk
12 cities
13 shoes
14 oil - rice
15 weather
16 homework
16 equipment
17 cats
18 rice
19 rooms
Đúng 2
Bình luận (0)
Giải hết giúp mik với ạ 🥺 từ câu 1 tới câu 19 đó ạ
Giúp mk từ câu 6 đến câu 19 vs ạ mk cần gấp c.ơn trc ạ
6. B
7. D
8. C
9. A
10. A
11. A
12. A
13. A
14. B
15. C
16. B
17. C
18. A
19. C
Đúng 0
Bình luận (0)
Câu 9:
d)-3/26 × (-15/19)+2/19×-3/26
GIÚP MÌNH Ạ,CHO MÌNH CẢM ƠN TRƯỚC Ạ 😊
\(d,-\dfrac{3}{26}.\left(-\dfrac{15}{19}\right)+\dfrac{2}{19}.\left(-\dfrac{3}{26}\right)\\=-\dfrac{3}{26}.\left(-\dfrac{15}{19}+\dfrac{2}{19}\right)\\ =-\dfrac{13}{19}.\left(-\dfrac{3}{26}\right)\\ =\dfrac{3}{38}. \)
Đúng 3
Bình luận (0)
d) \(\dfrac{-3}{26}\times\left(\dfrac{-15}{19}\right)+\dfrac{2}{19}\times\dfrac{-3}{26}\)
\(=\dfrac{-3}{26}\times\left[\left(\dfrac{-15}{19}\right)+\dfrac{2}{19}\right]\)
\(=\dfrac{-3}{26}\times\dfrac{-13}{19}\)
\(=\dfrac{3}{38}\)
Đúng 3
Bình luận (0)
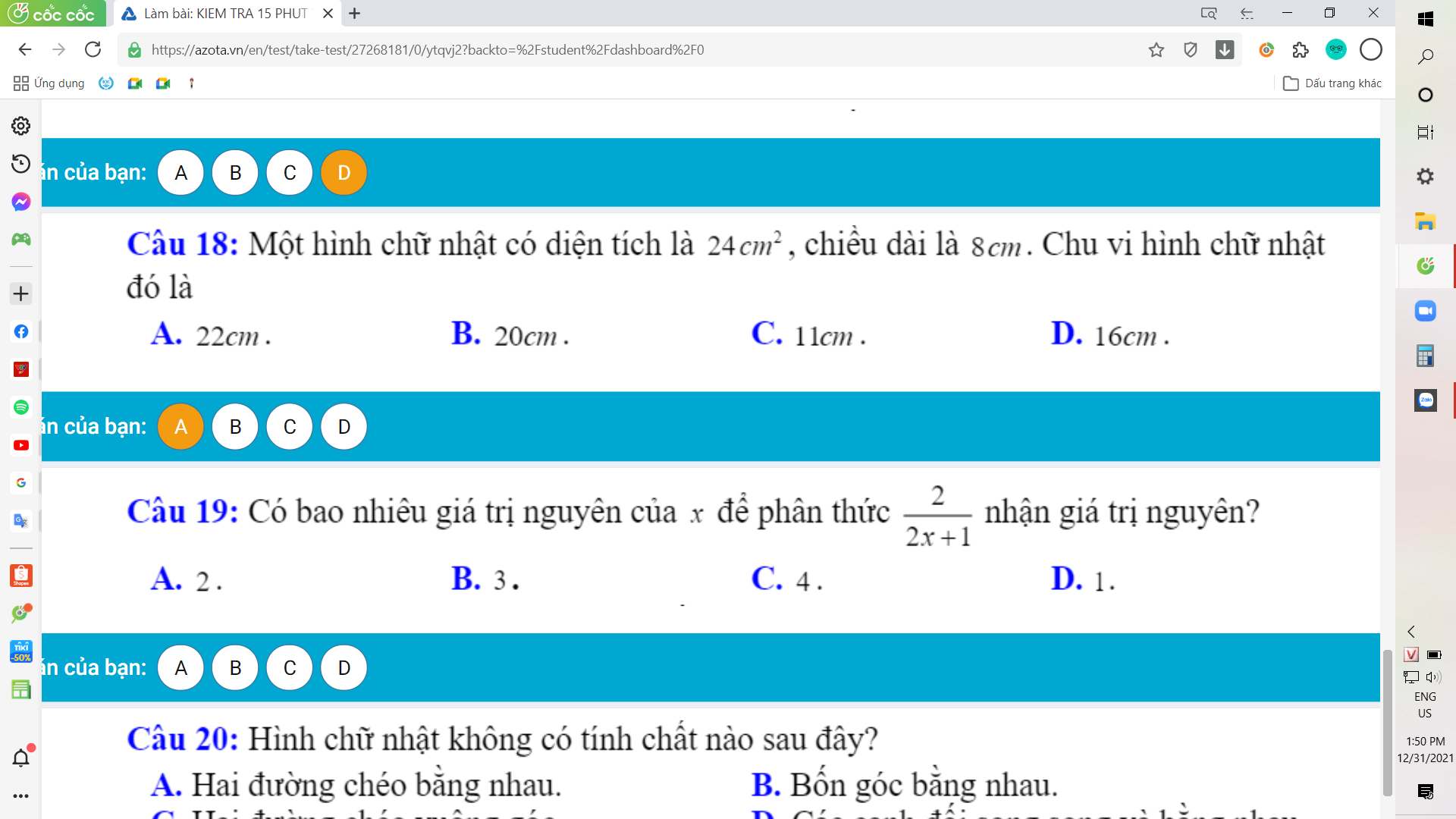 giúp mình câu 19 ạ
giúp mình câu 19 ạ
câu 18 19 20 ạ

Giúp e câu 19 đi ạ
Giúp em câu 18, 19 ạ 
Bài 17:
Áp dụng hệ thức lượng trong tam giác vuông vào ΔBAC vuông tại A có AH là đường cao ứng với cạnh huyền BC, ta được:
\(\left\{{}\begin{matrix}AB^2=BH\cdot BC\\AC^2=CH\cdot BC\end{matrix}\right.\)
\(\Leftrightarrow\dfrac{BH}{CH}=\dfrac{c^2}{b^2}\)
Đúng 0
Bình luận (0)
Giúp câu 17, 19 vs ạ
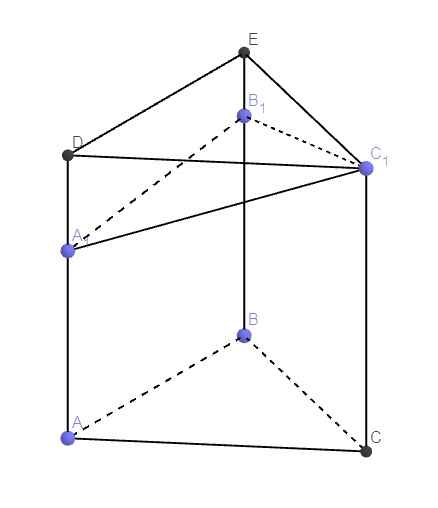
17.
Câu 17 này đề bài sai (ở độ dài AB, nếu ko nhìn lầm thì AB=41 là 1 con số phi lý)
Cách tính như sau:
Qua \(C_1\) kẻ các đường thẳng song song AC và BC, cắt \(AA_1\) và \(BB_1\) kéo dài tại D và E
\(\Rightarrow ABC.DEC_1\) là lăng trụ đứng có thể tích V
\(V=CC_1.S_{ABC}=6.\dfrac{AB^2\sqrt{3}}{4}=\dfrac{3AB^2\sqrt{3}}{2}\)
Gọi thể tích khối đa diện cần tính là \(V_1\)
\(\Rightarrow\dfrac{V_1}{V}=\dfrac{1}{3}\left(\dfrac{AA_1}{AD}+\dfrac{BB_1}{BE}+\dfrac{CC_1}{CC_1}\right)=\dfrac{5}{6}\)
\(\Rightarrow V_1=\dfrac{5}{6}V=...\)
Đúng 1
Bình luận (0)
19.
Gọi chiều cao hình hộp là y và cạnh đáy là x
\(\Rightarrow x^2y=6\Rightarrow y=\dfrac{6}{x^2}\)
\(S_đ=x^2\) ; \(S_{xq}=4xy=4x.\dfrac{6}{x^2}=\dfrac{24}{x}\)
\(\Rightarrow S_đ+S_{xq}=x^2+\dfrac{24}{x}=x^2+\dfrac{12}{x}+\dfrac{12}{x}\ge3\sqrt[3]{\dfrac{144x^2}{x^2}}=3\sqrt[3]{144}\)
Dấu "=" xảy ra khi \(x^2=\dfrac{12}{x}\Rightarrow x=\sqrt[3]{12}\)
Đúng 1
Bình luận (0)