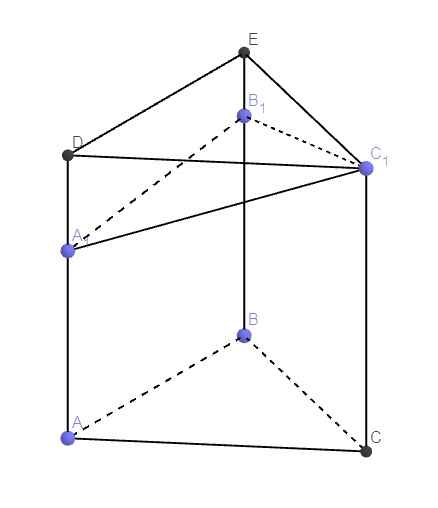
17.
Câu 17 này đề bài sai (ở độ dài AB, nếu ko nhìn lầm thì AB=41 là 1 con số phi lý)
Cách tính như sau:
Qua \(C_1\) kẻ các đường thẳng song song AC và BC, cắt \(AA_1\) và \(BB_1\) kéo dài tại D và E
\(\Rightarrow ABC.DEC_1\) là lăng trụ đứng có thể tích V
\(V=CC_1.S_{ABC}=6.\dfrac{AB^2\sqrt{3}}{4}=\dfrac{3AB^2\sqrt{3}}{2}\)
Gọi thể tích khối đa diện cần tính là \(V_1\)
\(\Rightarrow\dfrac{V_1}{V}=\dfrac{1}{3}\left(\dfrac{AA_1}{AD}+\dfrac{BB_1}{BE}+\dfrac{CC_1}{CC_1}\right)=\dfrac{5}{6}\)
\(\Rightarrow V_1=\dfrac{5}{6}V=...\)
19.
Gọi chiều cao hình hộp là y và cạnh đáy là x
\(\Rightarrow x^2y=6\Rightarrow y=\dfrac{6}{x^2}\)
\(S_đ=x^2\) ; \(S_{xq}=4xy=4x.\dfrac{6}{x^2}=\dfrac{24}{x}\)
\(\Rightarrow S_đ+S_{xq}=x^2+\dfrac{24}{x}=x^2+\dfrac{12}{x}+\dfrac{12}{x}\ge3\sqrt[3]{\dfrac{144x^2}{x^2}}=3\sqrt[3]{144}\)
Dấu "=" xảy ra khi \(x^2=\dfrac{12}{x}\Rightarrow x=\sqrt[3]{12}\)