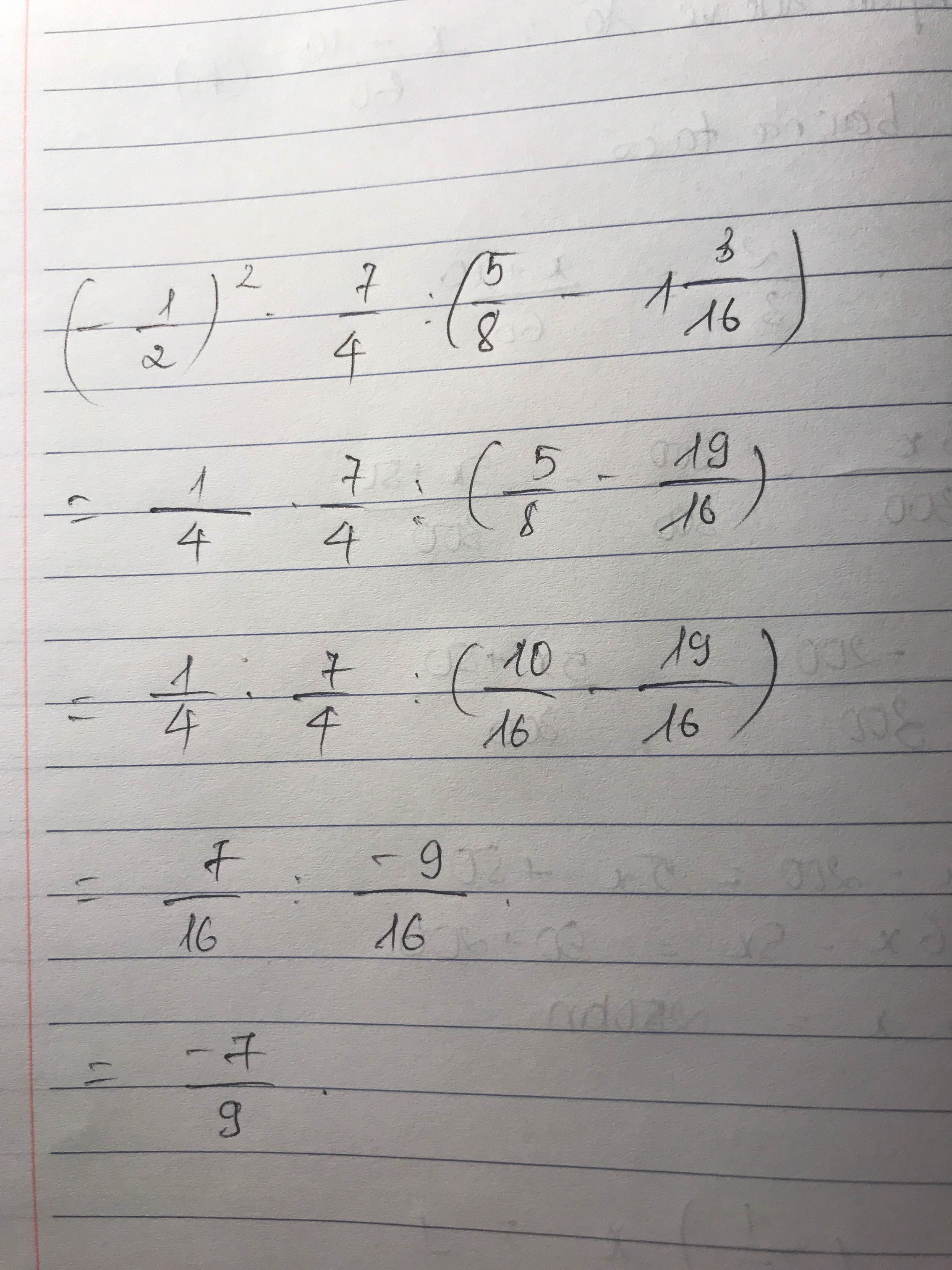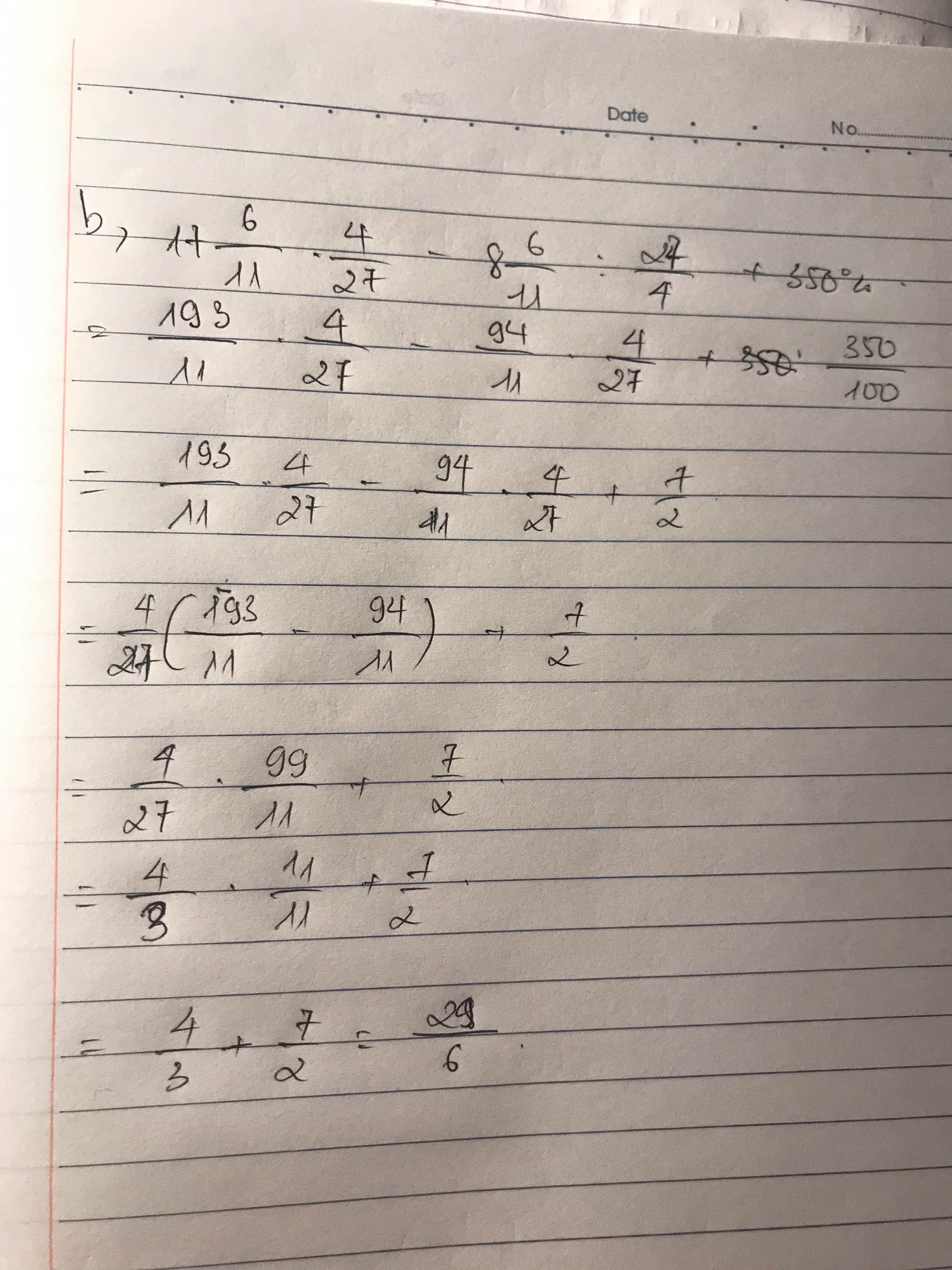Tính \(A=\dfrac{1}{2}+\dfrac{1}{4}+\dfrac{1}{8}+\dfrac{1}{16}+...+\dfrac{1}{2n}\)
Những câu hỏi liên quan
a)Tính tổng\(P=\dfrac{1}{1+2}+\dfrac{1}{1+2+3}+\dfrac{1}{1+2+3+4}+...+\dfrac{1}{1+2+3+...+2017}\)
b)CMR\(\dfrac{1}{4^2}+\dfrac{1}{6^2}+\dfrac{1}{8^2}+...+\dfrac{1}{\left(2n\right)^2}< \dfrac{1}{4}\)
\(a,P=\dfrac{1}{\left(2+1\right)\left(2+1-1\right):2}+\dfrac{1}{\left(3+1\right)\left(3+1-1\right):2}+...+\dfrac{1}{\left(2017+1\right)\left(2017+1-1\right):2}\\ P=\dfrac{1}{2\cdot3:2}+\dfrac{1}{3\cdot4:2}+...+\dfrac{1}{2017\cdot2018:2}\\ P=2\left(\dfrac{1}{2\cdot3}+\dfrac{1}{3\cdot4}+...+\dfrac{1}{2017\cdot2018}\right)\\ P=2\left(\dfrac{1}{2}-\dfrac{1}{3}+\dfrac{1}{3}-\dfrac{1}{4}+...+\dfrac{1}{2017}-\dfrac{1}{2018}\right)\\ P=2\left(\dfrac{1}{2}-\dfrac{1}{2018}\right)=2\cdot\dfrac{504}{1009}=\dfrac{1008}{1009}\)
\(b,\) Ta có \(\dfrac{1}{4^2}< \dfrac{1}{2\cdot4};\dfrac{1}{6^2}< \dfrac{1}{4\cdot6};...;\dfrac{1}{\left(2n\right)^2}< \dfrac{1}{\left(2n-2\right)2n}\)
\(\Leftrightarrow VT< \dfrac{1}{2\cdot4}+\dfrac{1}{4\cdot6}+...+\dfrac{1}{\left(2n-2\right)2n}\\ \Leftrightarrow VT< \dfrac{1}{2}\left(\dfrac{2}{2\cdot4}+\dfrac{2}{4\cdot6}+...+\dfrac{2}{\left(2n-2\right)2n}\right)\\ \Leftrightarrow VT< \dfrac{1}{2}\left(1-\dfrac{1}{4}+\dfrac{1}{4}-\dfrac{1}{6}+...+\dfrac{1}{2n-2}-\dfrac{1}{2n}\right)\\ \Leftrightarrow VT< \dfrac{1}{2}\left(1-\dfrac{1}{2n}\right)< \dfrac{1}{2}\cdot\dfrac{1}{2}=\dfrac{1}{4}\)
Đúng 1
Bình luận (0)
22 tháng 2 2022 lúc 16:48
a, Tính: M = \(1+\dfrac{1}{5}+\dfrac{3}{35}+...+\dfrac{3}{9603}+\dfrac{3}{9999}\)
b, Chứng tỏ: S = \(\dfrac{1}{4^2}+\dfrac{1}{6^2}+\dfrac{1}{8^2}+...+\dfrac{1}{\left(2n\right)^2}< \dfrac{1}{4}\left(n\in N,n\ge2\right)\)
a: \(M=\dfrac{6}{5}+\dfrac{3}{2}\left(\dfrac{2}{5\cdot7}+...+\dfrac{2}{97\cdot99}+\dfrac{2}{99\cdot101}\right)\)
\(=\dfrac{6}{5}+\dfrac{3}{2}\left(\dfrac{1}{5}-\dfrac{1}{101}\right)\)
\(=\dfrac{6}{5}+\dfrac{3}{10}-\dfrac{3}{202}=\dfrac{150}{101}\)
b: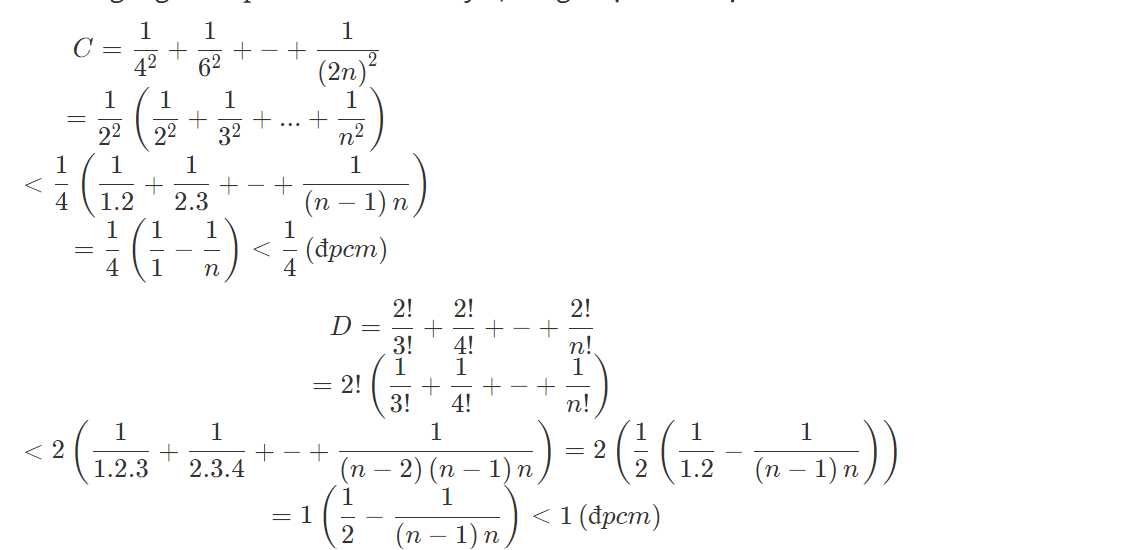 
Đúng 1
Bình luận (0)
tính nhanh \(\dfrac{1}{2}\) +\(\dfrac{1}{4}\) +\(\dfrac{1}{8}\)+\(\dfrac{1}{16}\) +.....+\(\dfrac{1}{512}\) +\(\dfrac{1}{1024}\)
Đặt A=1/2+1/4+1/8+..+1/1024
Ax2=1+1/2+1/4+1/8+..+1/512( Nhân cả 2 vế với 2)
Ax2-A=(1+1/2+1/4+1/8+..+1/512)-(1/2+1/4+1/8+..+1/1024)
<=>A=1-1/1024
<=>A=1023/1024
Vậy biểu thức đã cho = 1023/1024
Đúng 0
Bình luận (0)
\(\dfrac{1}{2}\)+\(\dfrac{1}{4}\)+\(\dfrac{1}{8}\)+\(\dfrac{1}{16}\)+\(\dfrac{1}{32}\)+\(\dfrac{1}{64}\)+\(\dfrac{1}{128}\)+\(\dfrac{1}{256}\)
Tính nhanh
Tính:
\(a,\dfrac{x+3}{2x-1}-\dfrac{x^2-5}{4x^2-4x+1}-\dfrac{2x^3+5x^2-x-1}{8x^3-12x^2+6x-1}\)
\(b,\dfrac{1}{1-x}+\dfrac{1}{1+x}+\dfrac{2}{1+x^2}+\dfrac{4}{1+x^4}+\dfrac{8}{1+x^8}+\dfrac{16}{1+x^{16}}\)
Cho A= \(\dfrac{1}{4^2}+\dfrac{1}{6^2}+\dfrac{1}{8^2}+\dfrac{1}{10^2}+...+\dfrac{1}{160^2}\)
Chứng minh: \(\dfrac{1}{8}< A< \dfrac{3}{16}\)
Thực hiện phép tính( tính nhanh nếu có thể)
a, \(\left(-\dfrac{1}{2}\right)^2.\dfrac{7}{4}:\left(\dfrac{5}{8}-1\dfrac{3}{16}\right)\)
b, \(17\dfrac{6}{11}.\dfrac{4}{27}-8\dfrac{6}{11}:\dfrac{27}{4}+350\%\)
a) Ta có: \(\left(\dfrac{-1}{2}\right)^2\cdot\dfrac{7}{4}:\left(\dfrac{5}{8}-1\dfrac{3}{16}\right)\)
\(=\dfrac{1}{4}\cdot\dfrac{7}{4}:\left(\dfrac{5}{8}-\dfrac{19}{16}\right)\)
\(=\dfrac{1}{4}\cdot\dfrac{7}{4}:\dfrac{-9}{16}\)
\(=\dfrac{1}{4}\cdot\dfrac{7}{4}\cdot\dfrac{-16}{9}\)
\(=\dfrac{-112}{144}=\dfrac{-7}{9}\)
b) Ta có: \(17\dfrac{6}{11}\cdot\dfrac{4}{27}-8\dfrac{6}{11}:\dfrac{27}{4}+350\%\)
\(=17\dfrac{6}{11}\cdot\dfrac{4}{27}-8\dfrac{6}{11}\cdot\dfrac{4}{27}+350\%\)
\(=\dfrac{4}{27}\left(17+\dfrac{6}{11}-8-\dfrac{6}{11}\right)+\dfrac{7}{2}\)
\(=\dfrac{4}{27}\cdot9+\dfrac{7}{2}\)
\(=\dfrac{4}{3}+\dfrac{7}{2}=\dfrac{8}{6}+\dfrac{21}{6}=\dfrac{29}{6}\)
Đúng 0
Bình luận (0)
a, \(\dfrac{1}{2}+\dfrac{1}{4}+\dfrac{1}{8}+\dfrac{1}{16}\) b, \(\dfrac{1}{2}+\dfrac{1}{3}+\dfrac{1}{5}\)
\(a,\dfrac{1}{2}+\dfrac{1}{4}+\dfrac{1}{8}+\dfrac{1}{16}=\dfrac{8}{16}+\dfrac{4}{16}+\dfrac{2}{16}+\dfrac{1}{16}=\dfrac{8+4+2+1}{16}=\dfrac{15}{16}\)
\(b,\dfrac{1}{2}+\dfrac{1}{3}+\dfrac{1}{5}=\dfrac{15}{30}+\dfrac{10}{30}+\dfrac{6}{30}=\dfrac{15+10+6}{30}=\dfrac{31}{30}\)
Đúng 2
Bình luận (0)
SGK Kết nối tri thức với cuộc sống - Trang 78
24 tháng 8 2023 lúc 0:41
Rút gọn rồi tính (theo mẫu).Mẫu: dfrac{5}{15}+dfrac{4}{3}dfrac{1}{3}+dfrac{4}{3}dfrac{1+4}{3}dfrac{5}{3}a) dfrac{21}{15}+dfrac{2}{5} b) dfrac{6}{16}+dfrac{1}{8} c) dfrac{3}{12}+dfrac{3}{4}
Đọc tiếp
Rút gọn rồi tính (theo mẫu).
| Mẫu: \(\dfrac{5}{15}+\dfrac{4}{3}=\dfrac{1}{3}+\dfrac{4}{3}=\dfrac{1+4}{3}=\dfrac{5}{3}\) |
a) \(\dfrac{21}{15}+\dfrac{2}{5}\) b) \(\dfrac{6}{16}+\dfrac{1}{8}\) c) \(\dfrac{3}{12}+\dfrac{3}{4}\)
a) \(\dfrac{21}{15}\) + \(\dfrac{2}{5}\) = \(\dfrac{9}{5}\)
b) \(\dfrac{6}{16}\) + \(\dfrac{1}{8}\) = \(\dfrac{1}{2}\)
c) \(\dfrac{3}{12}\) + \(\dfrac{3}{4}\) = 1
Đúng 0
Bình luận (0)