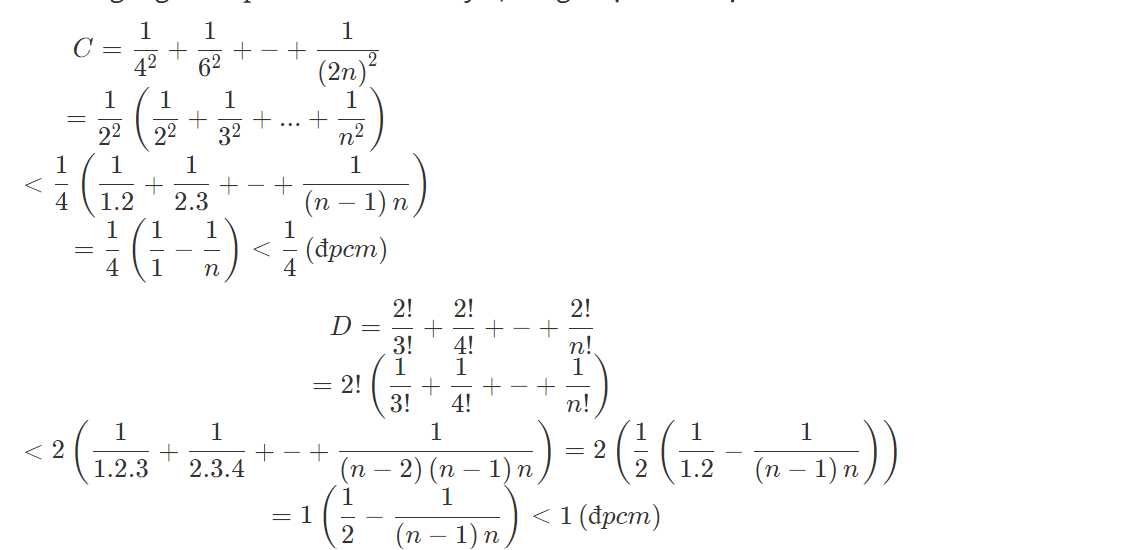Question

a, Tính: M = \(1+\dfrac{1}{5}+\dfrac{3}{35}+...+\dfrac{3}{9603}+\dfrac{3}{9999}\)

b, Chứng tỏ: S = \(\dfrac{1}{4^2}+\dfrac{1}{6^2}+\dfrac{1}{8^2}+...+\dfrac{1}{\left(2n\right)^2}< \dfrac{1}{4}\left(n\in N,n\ge2\right)\)

Answer 1

a: \(M=\dfrac{6}{5}+\dfrac{3}{2}\left(\dfrac{2}{5\cdot7}+...+\dfrac{2}{97\cdot99}+\dfrac{2}{99\cdot101}\right)\)

\(=\dfrac{6}{5}+\dfrac{3}{2}\left(\dfrac{1}{5}-\dfrac{1}{101}\right)\)

\(=\dfrac{6}{5}+\dfrac{3}{10}-\dfrac{3}{202}=\dfrac{150}{101}\)

b: