1: \(-1< =cosx< =1\)

=>\(-3< =3\cdot cosx< =3\)

=>\(y\in\left[-3;3\right]\)

2:

TXĐ là D=R

3: \(L=\lim\limits\dfrac{-3n^3+n^2}{2n^3+5n-2}\)

\(=\lim\limits\dfrac{-3+\dfrac{1}{n}}{2+\dfrac{5}{n^2}-\dfrac{2}{n^3}}=-\dfrac{3}{2}\)

4:

\(L=lim\left(3n^2+5n-3\right)\)

\(=\lim\limits\left[n^2\left(3+\dfrac{5}{n}-\dfrac{3}{n^2}\right)\right]\)

\(=+\infty\) vì \(\left\{{}\begin{matrix}lim\left(n^2\right)=+\infty\\\lim\limits\left(3+\dfrac{5}{n}-\dfrac{3}{n^2}\right)=3>0\end{matrix}\right.\)

5:

\(\lim\limits_{n\rightarrow+\infty}n^3-2n^2+3n-4\)

\(=\lim\limits_{n\rightarrow+\infty}n^3\left(1-\dfrac{2}{n}+\dfrac{3}{n^2}-\dfrac{4}{n^3}\right)\)

\(=+\infty\) vì \(\left\{{}\begin{matrix}\lim\limits_{n\rightarrow+\infty}n^3=+\infty\\\lim\limits_{n\rightarrow+\infty}1-\dfrac{2}{n}+\dfrac{3}{n^2}-\dfrac{4}{n^3}=1>0\end{matrix}\right.\)

\(1,y=3cosx\)

\(+TXD\) \(D=R\)

Có \(-1\le cosx\le1\)

\(\Leftrightarrow-3\le3cosx\le3\)

Vậy có tập giá trị \(T=\left[-3;3\right]\)

\(2,y=cosx\)

\(TXD\) \(D=R\)

\(3,L=lim\dfrac{n^2-3n^3}{2n^3+5n-2}=lim\dfrac{\dfrac{1}{n}-3}{2+\dfrac{5}{n^2}-\dfrac{2}{n^3}}\)(chia cả tử và mẫu cho \(n^3\))

\(=\dfrac{lim\dfrac{1}{n}-lim3}{lim2+5lim\dfrac{1}{n^2}-2lim\dfrac{1}{n^3}}=\dfrac{0-3}{2+5.0-2.0}=-\dfrac{3}{2}\)

\(4,L=lim\left(3n^2+5n-3\right)\\ =lim\left(3+\dfrac{5}{n}-\dfrac{3}{n^2}\right)\\ =lim3+5lim\dfrac{1}{n}-3lim\dfrac{1}{n^2}\\ =3\)

\(5,\lim\limits_{n\rightarrow+\infty}\left(n^3-2n^2+3n-4\right)\\ =lim\left(1-\dfrac{2}{n}+\dfrac{3}{n^2}-\dfrac{4}{n^3}\right)\\ =lim1-0\\ =1\)

ta có:

lim x → 0 x + 8 3 - x + 4 x = lim x → 0 x + 8 3 - 2 x - lim x → 0 x + 4 - 2 x = lim x → 0 1 x + 8 3 + 2 x + 8 3 + 4 + lim x → 0 1 x + 4 + 2 = 1 12 + 1 4 = 1 3

Đáp án B

Ta có:

Ta có: 

lim x → 2 x n + n x + n - 1 x - 1 2 = lim x → 2 x n - 1 - n x - 1 x - 1 2 = lim x → 1 x n - 1 + x n - 2 + . . + x + 1 - n x - 1 = lim x → 1 x n - 1 + x n - 2 + . . + x + 1 x - 1 = lim x → 1 x n - 1 + x n - 2 + . . + 1 + x n - 3 + x n - 4 + . . + 1 = n - 1 + n - 2 + . . + 1 = n n - 1 2 = n 2 - n 2

Đáp án C

Tìm hoành độ các giao điểm của hai đồ thị, ta có:

x 3 - x = x - x 3 <=> x 3 + x 2 - 2 x = 0

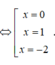
Vậy diện tích của hình phẳng tính là

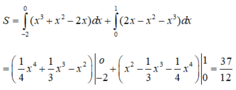
Vậy chọn đáp án B.

Ta có:

Đáp án B

Phương pháp:

Diện tích hình phẳng giới hạn bởi

đồ thị hàm số y=f(x),y=g(x), các đường thẳng 

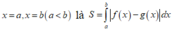
Cách giải:

Xét phương trình hoành độ giao điểm

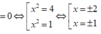
Chọn: A