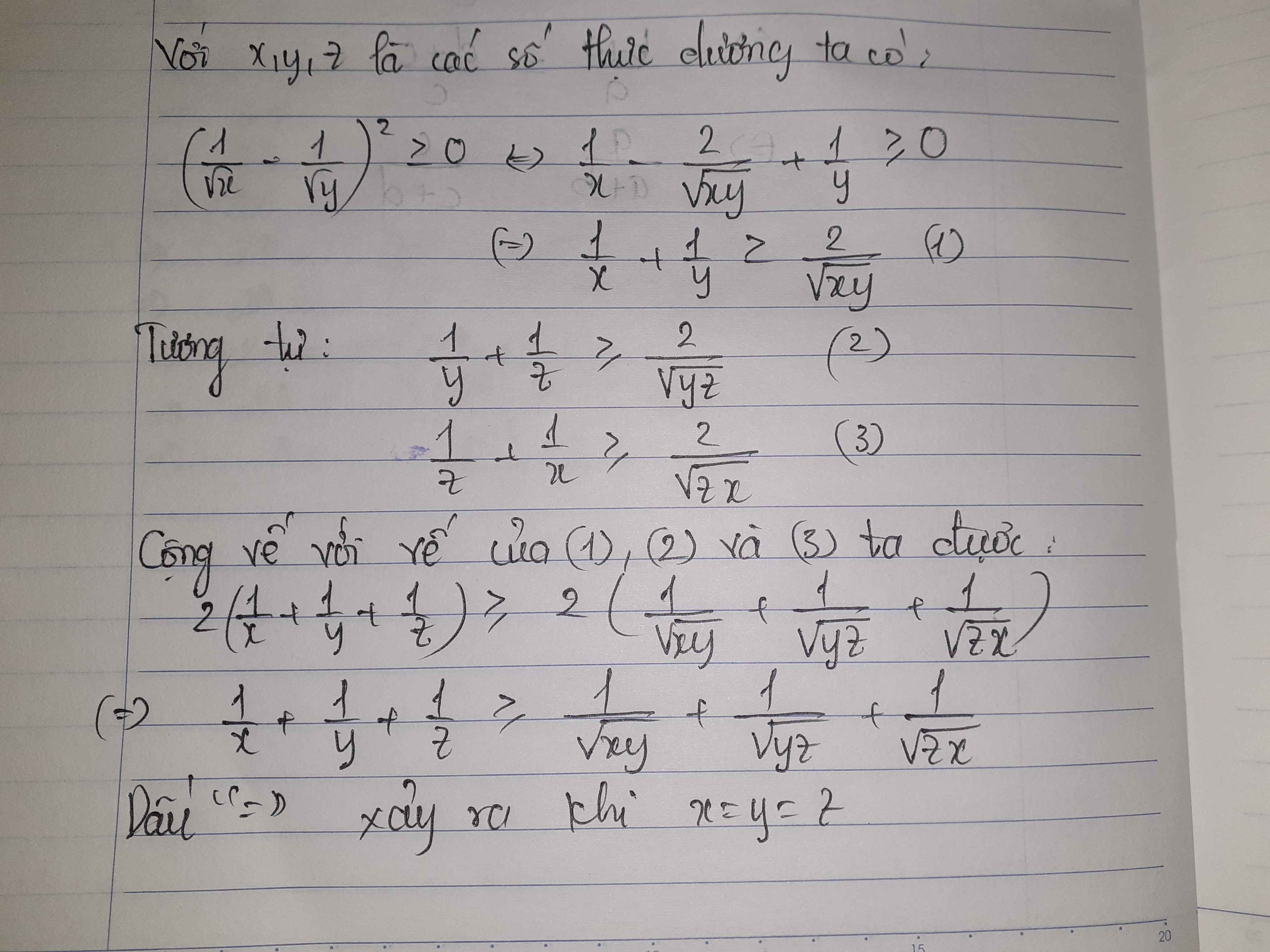\(\sqrt{x+yz}=\sqrt{x\left(x+y+z\right)+yz}=\sqrt{\left(x+y\right)\left(z+x\right)}\ge\sqrt{\left(\sqrt{xz}+\sqrt{xy}\right)^2}=\sqrt{xy}+\sqrt{xz}\)

\(\Rightarrow\dfrac{x}{x+\sqrt{x+yz}}\le\dfrac{x}{x+\sqrt{xy}+\sqrt{xz}}=\dfrac{\sqrt{x}}{\sqrt{x}+\sqrt{y}+\sqrt{z}}\)

Tương tự:

\(\dfrac{y}{y+\sqrt{y+xz}}\le\dfrac{\sqrt{y}}{\sqrt{x}+\sqrt{y}+\sqrt{z}}\)

\(\dfrac{z}{z+\sqrt{z+xy}}\le\dfrac{\sqrt{z}}{\sqrt{x}+\sqrt{y}+\sqrt{z}}\)

Cộng vế:

\(VT\le\dfrac{\sqrt{x}+\sqrt{y}+\sqrt{z}}{\sqrt{x}+\sqrt{y}+\sqrt{z}}=1\)

Dấu "=" xảy ra khi \(x=y=z=\dfrac{1}{3}\)

Đặt vế trái của BĐT cần chứng minh là P

Ta có:

\(P=\dfrac{\sqrt{xy+\left(x+y+z\right)z}+\sqrt{2\left(x^2+y^2\right)}}{1+\sqrt{xy}}=\dfrac{\sqrt{\left(x+z\right)\left(y+z\right)}+\sqrt{2\left(x^2+y^2\right)}}{1+\sqrt{xy}}\)

\(P\ge\dfrac{\sqrt{\left(\sqrt{xy}+z\right)^2}+\sqrt{\left(x+y\right)^2}}{1+\sqrt{xy}}=\dfrac{\sqrt{xy}+x+y+z}{1+\sqrt{xy}}=\dfrac{\sqrt{xy}+1}{1+\sqrt{xy}}=1\) (đpcm)

Dấu "=" xảy ra khi \(x=y\)

Lời giải:

Sử dụng PP biến đổi tương đương kết hợp với BĐT Cauchy:

Ta có: \(\frac{1}{xy}+\frac{1}{xz}\geq 1\Leftrightarrow \frac{z}{xyz}+\frac{y}{xyz}\geq 1\)

\(\Leftrightarrow \frac{y+z}{xyz}\geq 1\Leftrightarrow y+z\geq xyz\)

\(\Leftrightarrow y+z\geq (4-y-z)yz\)

\(\Leftrightarrow y^2z+yz^2+y+z\geq 4yz(*)\)

Thật vậy, áp dụng BĐT Cauchy ta có:

\(\left\{\begin{matrix} y^2z+z\geq 2\sqrt{y^2z^2}=2yz\\ yz^2+y\geq 2\sqrt{z^2y^2}=2yz\end{matrix}\right.\)

Cộng theo vế: \(y^2z+yz^2+y+z\geq 4yz\). Do đó $(*)$ đúng. Ta có đpcm.

Dấu bằng xảy ra khi \((x,y,z)=(2,1,1)\)

Chứng minh gì bạn?

chtt

em thó nhé sir:)) đang rảnh

\(\dfrac{1}{x}\left(\dfrac{1}{y}+\dfrac{1}{z}\right)\ge\dfrac{4}{x\left(y+z\right)}\ge\dfrac{4}{\dfrac{\left(x+y+z\right)^2}{4}}=\dfrac{16}{\left(x+y+z\right)^2}=1\)

Có \(VT=\dfrac{x^2}{x^3-xyz+2013x}+\dfrac{y^2}{y^3-xyz+2013y}+\dfrac{z^2}{z^3-xyz+2013z}\)

\(\ge\dfrac{\left(x+y+z\right)^2}{x^3+y^3+z^3-3xyz+2013\left(x+y+z\right)}\)

\(=\dfrac{\left(x+y+z\right)^2}{\left(x+y+z\right)\left[x^2+y^2+z^2-\left(xy+yz+zx\right)\right]+2013\left(x+y+z\right)}\)

\(=\dfrac{x+y+z}{x^2+y^2+z^2-\left(xy+yz+zx\right)+3\left(xy+yz+zx\right)}\) 

(vì \(2013=3.671=3\left(xy+yz+zx\right)\))

\(=\dfrac{x+y+z}{x^2+y^2+z^2+2\left(xy+yz+zx\right)}\)

\(=\dfrac{x+y+z}{\left(x+y+z\right)^2}\)

\(=\dfrac{1}{x+y+z}\)

ĐTXR \(\Leftrightarrow\dfrac{1}{x^2-yz+2013}=\dfrac{1}{y^2-zx+2013}=\dfrac{1}{z^2-xy+2013}\)

\(\Leftrightarrow x^2-yz=y^2-zx=z^2-xy\)

\(\Leftrightarrow x=y=z\) (với \(x,y,z>0\))

Vậy ta có đpcm.

\(\dfrac{1}{x}+\dfrac{1}{y}+\dfrac{1}{z}\ge\dfrac{1}{\sqrt{xy}}+\dfrac{1}{\sqrt{yz}}+\dfrac{1}{\sqrt{zx}}\)

\(\Rightarrow\dfrac{2}{x}+\dfrac{2}{y}+\dfrac{2}{z}\ge\dfrac{2}{\sqrt{xy}}+\dfrac{2}{\sqrt{yz}}+\dfrac{2}{\sqrt{zx}}\)

\(\Rightarrow\dfrac{2}{x}+\dfrac{2}{y}+\dfrac{2}{z}-\dfrac{2}{\sqrt{xy}}+\dfrac{2}{\sqrt{yz}}+\dfrac{2}{\sqrt{zx}}\ge0\)

\(\Rightarrow\dfrac{1}{x}-\dfrac{2}{\sqrt{xy}}+\dfrac{1}{y}+\dfrac{1}{y}-\dfrac{2}{\sqrt{yz}}+\dfrac{1}{z}+\dfrac{1}{z}-\dfrac{2}{\sqrt{zx}}+\dfrac{1}{x}\ge0\)

\(\Rightarrow\left(\dfrac{1}{\sqrt{x}}-\dfrac{1}{\sqrt{y}}\right)^2+\left(\dfrac{1}{\sqrt{y}}-\dfrac{1}{\sqrt{z}}\right)^2+\left(\dfrac{1}{\sqrt{z}}-\dfrac{1}{\sqrt{x}}\right)^2\ge0\) (luôn đúng)

Dấu = xảy ra khi \(x=y=z\)

\(\left(x+y+z\right)^2=x^2+y^2+z^2+2xy+2xz+2yz=z^2+\left(x+y\right)^2+2z\left(x+y\right)=36\)

áp dụng BĐT cosi : 

\(z^2+\left(x+y\right)^2\ge2z\left(x+y\right)\)

<=> \(z^2+\left(x+y\right)^2+2z\left(x+y\right)\ge4z\left(x+y\right)=36< =>z\left(x+y\right)\ge9\)

ta lại có \(\dfrac{x+y}{xyz}=\dfrac{x}{xyz}+\dfrac{y}{xyz}=\dfrac{1}{yz}+\dfrac{1}{xz}\) áp dụng BĐT buhihacopxki dạng phân thức => \(\dfrac{1}{yz}+\dfrac{1}{xz}\ge\dfrac{4}{yz+xz}=\dfrac{4}{z\left(x+y\right)}\ge\dfrac{4}{9}\left(đpcm\right)\)

dấu bằng xảy ra khi \(\left[{}\begin{matrix}yz=xz< =>x=y\\x+y+z=6\\z^2=\left(x+y\right)^2\end{matrix}\right.< =>\left[{}\begin{matrix}x+y+z=6\\z=2x=2y\end{matrix}\right.< =>\left[{}\begin{matrix}x=y=\dfrac{3}{2}\\z=3\end{matrix}\right.\)

\(\dfrac{x+y}{xyz}=\dfrac{1}{yz}+\dfrac{1}{xz}\).

Áp dụng bất đẳng thức Cauchy-Schawrz dạng Engel:

\(\dfrac{1}{yz}+\dfrac{1}{xz}\ge\dfrac{4}{z\left(x+y\right)}\)     (1).

Áp dụng bất đẳng thức Cauchy cho hai số dương z và x+y, ta có:

\(z\left(x+y\right)\le\left(\dfrac{x+y+z}{2}\right)^2=9\). Suy ra, \(\dfrac{4}{z\left(x+y\right)}\ge\dfrac{4}{9}\)     (2).

Từ (1) và (2), suy ra \(\dfrac{x+y}{xyz}\ge\dfrac{4}{9}\) (đpcm).

Dấu "=" xảy ra khi và chỉ khi \(\dfrac{1}{yz}=\dfrac{1}{xz}\) và \(z=x+y\).