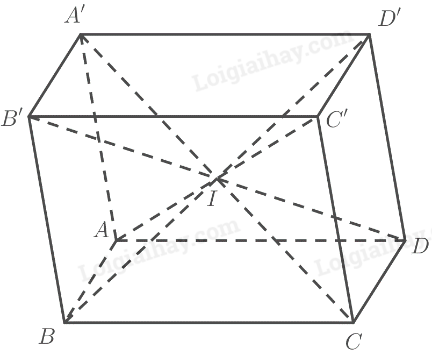
Trong không gian Oxyz, cho hình lập phương ABCD.A'B'C'D' với \(A\left(0;0;0\right),B\left(1;0;0\right),D\left(0;1;0\right),A'\left(0;0;1\right)\)
a) Hãy tìm tọa độ các đỉnh còn lại
b) Chứng minh \(A'C\perp\left(BC'D\right)\)
c) Tìm tọa độ của chân đường vuông góc chung của B'D và BC'