+ Nếu m = 0 thì bất phương trình nghiệm đúng với mọi x;

    + Nếu m = -2 thì bất phương tình trở thành – 4x + 2 > 0, không nghiệm đúng với mọi x.

    + Nếu m ≠ 0 và m ≠ -2 thì bất phương trình nghiệm đúng với mọi x khi và chỉ khi

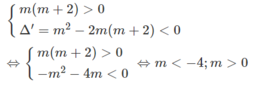
Đáp số: m < -4; m ≥ 0

Theo Vi-ét:\(\left\{{}\begin{matrix}x_1+x_2=2m\\x_1x_2=m^2+6m+10\end{matrix}\right.\)

\(P=x^2_1+x^2_2-x_1x_2\\ =\left(x_1+x_2\right)^2-3x_1x_2\\ =\left(2m\right)^2-3\left(m^2+6m+10\right)\\ =4m^2-3m^2-18m-30\\ =m^2-18m-30\\ =\left(m^2-18m+81\right)-111\\ =\left(m-9\right)^2-111\ge-111\)

Dấu "=" xảy ra\(\Leftrightarrow m=9\)

Vậy \(P_{min}-111\Leftrightarrow m=9\)

\(\Delta'=\left(-m\right)^2-\left(m^2-6m-10\right)=m^2-m^2-6m-10=-6m-10\)

Để pt có 2 nghiệm thì\(\Delta'\ge0\Rightarrow-6m-10\ge0\Rightarrow6m+10\le0\Rightarrow m\le-\dfrac{5}{3}\)

Chọn A.

+ Điều kiện cần: Giả sử phương trình đã cho có ba nghiệm phân biệt x₁; x₂; x₃ lập thành một cấp số nhân.

Theo định lý Vi-ét, ta có x₁.x₂.x₃ = 64

Theo tính chất của cấp số nhân, ta có x₁x₃ = x₂². Suy ra ta có x₂³ = 64 ⇔ x₂ = 4

Thay x = 4 vào phương trình đã cho ta được: 4³ – 7m.4² + 2(m² + 6m).4 – 64 = 0

⇔ m² – 8m = 0

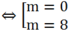
+ Điều kiện đủ: Với m = 0  thay vào phương  trình đã cho ta được: x³ – 64 = 0 hay x = 4

(nghiệm kép-loại)

Với m = 8 thay vào phương trình đã cho nên ta có phương trình x³ – 56x² + 224x – 64 = 0   

Giải phương trình này, ta được 3  nghiệm phân biệt lập thành cấp số nhân.

Vậy m = 8 là giá trị cần tìm.

PT $(*)$ là PT bậc nhất ẩn $x$ thì làm sao mà có $x_1,x_2$ được hả bạn?

PT cuối cũng bị lỗi.

Bạn xem lại đề!

Lời giải:

a) 

Ta có: $\Delta'=m^2-(2m-2)=m^2-2m+2=(m-1)^2+1>0$ với mọi $m\in\mathbb{R}$

Do đó pt luôn có 2 nghiệm phân biệt $x_1,x_2$ với mọi $m\in\mathbb{R}$

b) 

Áp dụng định lý Viet: \(\left\{\begin{matrix} x_1+x_2=-2m\\ x_1x_2=2m-2\end{matrix}\right.\)

Để $x_1^2+x_2^2-3x_1x_2=4$

$\Leftrightarrow (x_1+x_2)^2-5x_1x_2=4$

$\Leftrightarrow (-2m)^2-5(2m-2)=4$

$\Leftrightarrow 4m^2-10m+6=0$

$\Leftrightarrow 2m^2-5m+3=0$

$\Leftrightarrow (m-1)(2m-3)=0$

$\Rightarrow m=1$ hoặc $m=\frac{3}{2}$ (đều thỏa mãn)

Để pt có 2 nghiệm phân biệt thì \(\Delta'=m^2-\left(m+2\right)>0\Leftrightarrow\left(m+1\right)\left(m-2\right)>0\Leftrightarrow\left[{}\begin{matrix}m>2\\m< -1\end{matrix}\right.\). (1)

Khi đó theo hệ thức Viète ta có \(\left\{{}\begin{matrix}x_1+x_2=2m\\x_1x_2=m+2\end{matrix}\right.\).

Ta có \(x_1^3+x_2^3=\left(x_1+x_2\right)^3-3x_1x_2\left(x_1+x_2\right)=\left(2m\right)^3-3.2m.\left(m+2\right)=8m^3-6m^2-12m\).

Do đó \(8m^3-6m^2-12m\le16\Leftrightarrow\left(m-2\right)\left(8m^2+10m+8\right)\le0\Leftrightarrow m\le2\)

(do \(8m^2+10m+8=2\left(2m+\dfrac{5}{4}\right)^2+\dfrac{39}{8}>0\forall m\)).

Kết hợp vs (1) ta có m < -1.

Bạn ơi, bạn xem lại đề có được không ạ? Là \(\left(x_1^2-2mx_1+3\right)\left(x_2^2-2mx_2-2\right)=50\) hay sao ạ?

a: Δ=(-2m)^2-4(m-2)

=4m^2-4m+8=(2m-1)^2+7>=7>0

=>PT luôn có hai nghiệm phân biệt

b: x1^2+x2^2-6x1x2

=(x1+x2)^2-8x1x2

=(2m)^2-8(m-2)

=4m^2-8m+16=(2m-2)^2+8>=8

=>24/(2m-2)^2+8<=3

=>M>=-3

Dấu = xảy ra khi m=1