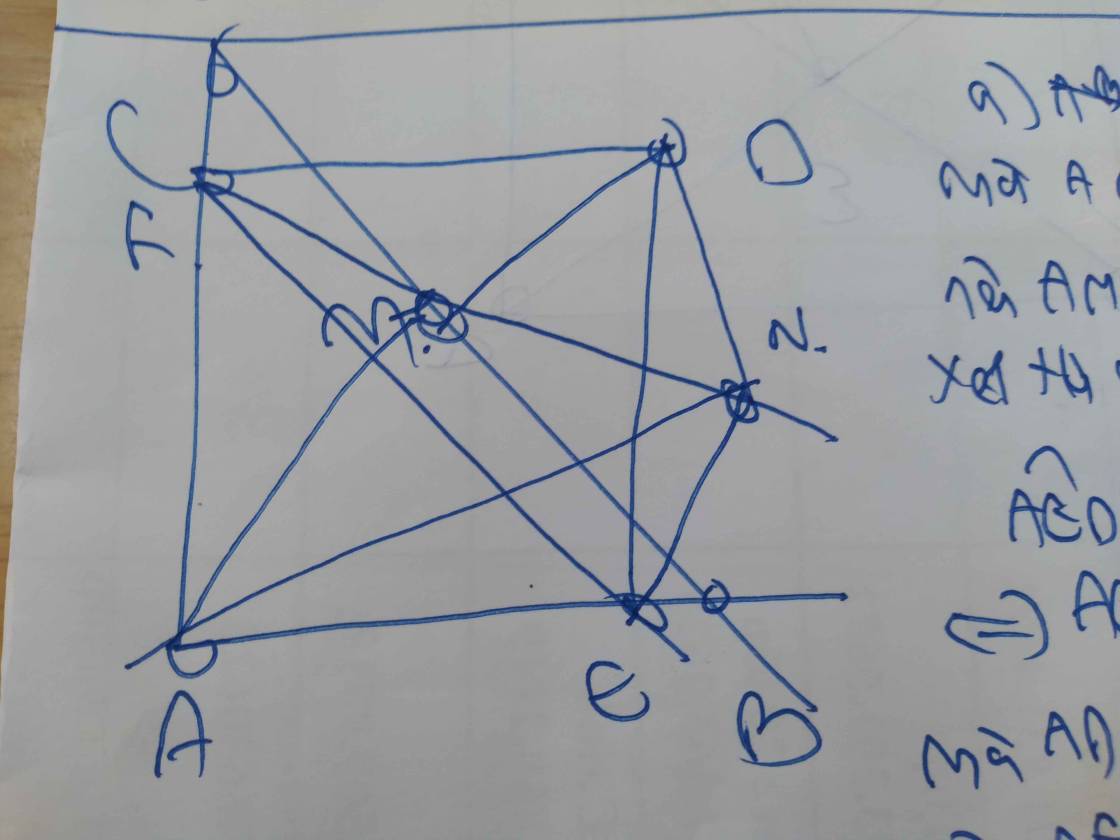
Cho hình thang $A B C D$ có $\widehat{A}=\widehat{D}=90^{\circ}, A D=4 A B, C D=3 A B$. Gọi $M$ là trung điểm của $A D, E$ là hình chiếu vuông góc của $M$ lên $B C$. Tia $B M$ cắt đường thẳng $C D$ tại $F$.
a) Chứng minh rằng $\widehat{M A E}=\widehat{M B E}$.
b) Chứng minh rằng $A B D F$ là hình bình hành.
c) Đường thẳng qua $M$ vuông góc với $B F$ cắt cạnh $B C$ tại $N$. Gọi $H$ là hình chiếu vuông góc của $N$ lên $C D$. Chứng minh rằng tam giác $B N F$ cân.
d) Chứng minh rằng đường thẳng $M H$ đi qua trung điểm của $D E$.

Những câu hỏi liên quan
Cho hình thang vuông ABCD(AB//CD), góc A=góc D=90 có AB=AD, góc C=45 gọi E là điểm đối xứng của B qua A, G là điểm đối xứng của C qua D. H là trung điểm của FG. Tia BH cắt CD tại K.
a)c/m BEFD là hình vuông và E,B,C thẳng hàng
b)c/m tam giác CFK cân
cho tam giác ABC vuông cân tại A. Gọi M là trung điểm BC. Trên tia đối MA lấy điểm D từ D kẻ đường thẳng vuông góc với AB, AC lần lượt tại E, F a) c/m tg AEDF là hình vuông. b) c/m EF // BC. c) Qua E kẻ đường thẳng vuông góc với MF. c/m \(\widehat{AND}\) = 40o
Cho tam giác ABC vuông tại A (ACAB). Gọi H là hình chiếu của A trên BC, D là điểm nằm trên đoạn AH (D khác A,D khác H). Đường thẳng BD cắt đường tròn tâm C bán kính CA tại E và F(F nằm giữa B và D); M là điểm trên đoạn AB sao cho widehat{ACF}2.widehat{BFM}; MF cắt AH tại Na) C/m: BH.BCBE.BF và tứ giác EFHC nội tiếp đường trònb) C/m: HD là phân giác góc EHFc) C/m: F là trung điểm MN
Đọc tiếp
Cho tam giác ABC vuông tại A (AC<AB). Gọi H là hình chiếu của A trên BC, D là điểm nằm trên đoạn AH (D khác A,D khác H). Đường thẳng BD cắt đường tròn tâm C bán kính CA tại E và F(F nằm giữa B và D); M là điểm trên đoạn AB sao cho \(\widehat{ACF}=2.\widehat{BFM}\); MF cắt AH tại N
a) C/m: BH.BC=BE.BF và tứ giác EFHC nội tiếp đường tròn
b) C/m: HD là phân giác góc EHF
c) C/m: F là trung điểm MN
Xin lỗi bạn nha ! Vì lỗi nên mình không vẽ được hình cho bạn ,có j bạn tự vẽ nha !!!
Bài giải
a) AB là tiếp tuyến tại A của ( C)
=> \(\widehat{BAF}=\widehat{AEF}\)
Xét \(\Delta ABF\)và \(\Delta EBA\)có :
\(\hept{\begin{cases}\widehat{ABE}chung\\\widehat{BAF}=\widehat{BEA}\end{cases}\Rightarrow\Delta ABF}\infty\Delta EBA\left(g-g\right)\)
\(\Rightarrow\frac{AB}{BE}=\frac{BF}{AB}\Rightarrow AB^2=BE.BF\)
Xét \(\Delta ABC\) vuông tại A có đường cao AH .
=> AB2 =BH . BC
=> BH . BC = BE . BF ( =AB2 )
Xét \(\Delta BHF\)và \(\Delta BEC\)có :
\(\frac{BH}{BE}=\frac{BF}{BC}\)
\(\widehat{CBE}\)chung
=> \(\Delta BHF\infty\Delta BEC\left(c-g-c\right)\)
=> \(\widehat{BHF}=\widehat{BEC}\)
*) \(\widehat{BHF}+\widehat{FHC}=\widehat{BEC}+\widehat{FHC}\)
\(\Leftrightarrow\widehat{FEC}+\widehat{FHC}=\widehat{BHC}=180^O\)
=> EFHC là tứ giác nội tiếp ( có tổng 2 góc đối =180 o
b) EFHC là tứ giác nội tiếp
=> \(\widehat{EHC}=\widehat{EFC}\)( cùng chắn góc EC )
\(\widehat{FEC}=\widehat{BHF}\)( c/ m cân A )
Mà \(\widehat{FEC}=\widehat{EFC}\)( \(\Delta ECF\)cân ở C )
=> \(\widehat{EHC}=\widehat{BHF}\)
=> 90O \(-\widehat{EHC}=90^O-\widehat{BHF}\)
<=> \(\widehat{EHD}=\widehat{FHD}\)
=> HD là phân giác góc EHF
Bạn giải câu c dùm mình được không?
Mình không biết làm ,xin lỗi bạn nhiều nha ,mình xin lỗi bạn rất nhiều khi không đáp ứng được nhu cầu của bạn ,mình thành thật xin lỗi bạn rất rất nhiều !!! Bạn xem trong danh sách kết bạn ý ,mình có ghi đó !!
Xem thêm câu trả lời
Cho tứ giác ABCD. Có G là trung điểm của đoạn nối các trung điểm của hai đường chéo AC và BD. Gọi m là một đường thẳng không cắt cạnh nào hình thang ABCD; Gọi A',B',C',D',G' lần lượt là hình chiếu của A,B,C,D,G lên đường thẳng m. Chứng minh GG'=1/4 (AA' +BB' +CC' +DD')
Cho tứ giác ABCD. Có G là trung điểm của đoạn nối các trung điểm của hai đường chéo AC và BD. Gọi m là một đường thẳng không cắt cạnh nào hình thang ABCD; Gọi A',B',C',D',G' lần lượt là hình chiếu của A,B,C,D,G lên đường thẳng m. Chứng minh GG'=1/4 (AA' BB' CC' DD')
(Thừa Thiên Huế - 2020)
Cho đường tròn tâm $O$ đường kính $AB$. Trên đường tròn $(O)$ lấy điểm $C$ không trùng $B$ sao cho $AC BC$. Các tiếp tuyến của đường tròn $(O)$ tại $A$ và tại $C$ cắt nhau tại $D$. Gọi $H$ là hình chiếu vuông góc của $C$ trên $AB$, $E$ là giao điểm của hai đường thẳng $OD$ và $AC$.
a. Chứng minh $OECH$ là tứ giác nội tiếp.
b. Gọi $F$ là giao điểm của hai đường thẳng $CD$ và $AB$. Chứng minh $2widehat{BCF} + widehat{CFB} 90^{circ}$.
c. Gọi $M$ là giao điểm của hai đư...
Đọc tiếp
(Thừa Thiên Huế - 2020)
Cho đường tròn tâm $O$ đường kính $AB$. Trên đường tròn $(O)$ lấy điểm $C$ không trùng $B$ sao cho $AC > BC$. Các tiếp tuyến của đường tròn $(O)$ tại $A$ và tại $C$ cắt nhau tại $D$. Gọi $H$ là hình chiếu vuông góc của $C$ trên $AB$, $E$ là giao điểm của hai đường thẳng $OD$ và $AC$.
a. Chứng minh $OECH$ là tứ giác nội tiếp.
b. Gọi $F$ là giao điểm của hai đường thẳng $CD$ và $AB$. Chứng minh $2\widehat{BCF} + \widehat{CFB} = 90^{\circ}$.
c. Gọi $M$ là giao điểm của hai đường thẳng $BD$ và $CH$. Chứng minh hai đường thẳng $EM$ và $AB$ song song với nhau.
DC = DA
OA = OC
Do đó OD là trung trực của đoạn thẳng AC : suy ra OD vuông góc với AC
Tứ giác OECH có góc CEO + góc CHO = 180 độ
Suy ra tứ giác OECH là tứ giác nội tiếp
Cho nửa đường tròn tâm O đường kính AB. d là tiếp tuyến tại A của (O). D là điểm thay đổi trên d, BD cắt (O) tại điểm C. Gọi M là trung điểm AD. Gọi E là hình chiếu vuông góc của A trên OD.
a/ CM : \(\widehat{CEB}=2\widehat{CAB}\)
b/ AE cắt MC tại N. CM : N thuộc 1 đường thẳng cố định
Cho tứ giác ABCD. Có G là trung điểm của đoạn nối các trung điểm của hai đường chéo AC và BD. Gọi m là một đường thẳng không cắt cạnh nào của hình thang ABCD; Gọi A, B, C’, D’, G lần lượt là hình chiếu của A, B, C, D, G lên đường thẳng m. Chứng minh GG 0.5(AA+BB+CC+DD’)
Đọc tiếp
Cho tứ giác ABCD. Có G là trung điểm của đoạn nối các trung điểm của hai đường chéo AC và BD. Gọi m là một đường thẳng không cắt cạnh nào của hình thang ABCD; Gọi A', B', C’, D’, G' lần lượt là hình chiếu của A, B, C, D, G lên đường thẳng m. Chứng minh GG' = 0.5(AA'+BB'+CC'+DD’)
Gọi E và F lần lượt là trung điểm của AC và BD; E' và F' lần lượt là hình chiếu của E, F trên đường thẳng m.
Khi đó, GG' là đường trung bình của hình thang EE'F'F

⇒ G G ' = 1 2 EE' +FF').
Mà EE' và FF' lần lượt là đường trung bình của hình thang AA'C'C và BB'D'D.
⇒ EE ' = 1 2 (AA' +CC') và FF ' = 1 2 (BB' +DD')
Thay vào (1) ta được ĐPCM
Đúng 0
Bình luận (0)
Gọi d là đường thẳng đi qua A(2;0) có hệ số góc m cắt đồ thị
C
:
y
−
x
3
+
6
x
2
−
9
x
+
2
tại ba điểm phân biệt A,B,C Gọi B,C lần lượt là hình chiếu vuông góc của B,C lên trục tung. Tìm giá trị dương của m để hình thang BBCC có diện tích A. m1 B.
m
1
2...
Đọc tiếp
Gọi d là đường thẳng đi qua A(2;0) có hệ số góc m cắt đồ thị C : y = − x 3 + 6 x 2 − 9 x + 2 tại ba điểm phân biệt A,B,C Gọi B',C' lần lượt là hình chiếu vuông góc của B,C lên trục tung. Tìm giá trị dương của m để hình thang BB'C'C có diện tích
A. m=1
B. m = 1 2
C.m=2
D. m = 3 2
Đáp án là C.
Không mất tính tổng quát, giả sử
x C > x B .
Ta có: d có phương trình
y = m x − 2 .
Phương trình hoành độ giao điểm:
m x − 2 = − x 3 + 6 x 2 − 9 x + 2
⇔ x = 2 x 2 − 4 x + 1 + m = 0
Để tồn tại A, B, thì phương trình x 2 − 4 x + m + 1 = 0 phải có 2 nghiệm phân biệt khác 2
⇔ m < 3 ⇒ x A = 2 ; x B + x C = 4 ; x B x C = m + 1 ; y C − y B = m x C − x B .
Trường hợp 1: ⇒ x B x C = m + 1 > 0 ⇔ − 1 < m < 3 * .
Ta có .
S B B ' C ' C = B B ' + C C ' . B ' C ' 2 = x B + x C . m x C − x B 2 = 8 ⇔ 4 m 16 − 4 m + 1 2 = 8
.
Đối chiếu điều kiện (*) ta được m=2.
Trường hợp 2:
x C > 0 > x B ⇒ x B x C = m + 1 < 0 ⇔ m < − 1 < 0
(Loại vì m > 0 ).
Đúng 0
Bình luận (0)