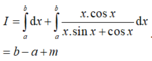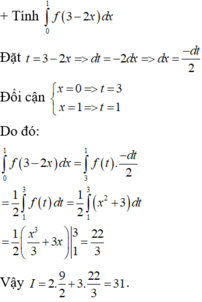Tìm (sin x + 1)⅓ cosxdx

Những câu hỏi liên quan
Cho hàm số yf(x) liên tục trên R thỏa mãn
∫
1
9
f
(
x
)
x
d
x
4
,
∫
0
π
2
f
(
sin
x
)
c
o
s
x...
Đọc tiếp
Cho hàm số y=f(x) liên tục trên R thỏa mãn ∫ 1 9 f ( x ) x d x = 4 , ∫ 0 π 2 f ( sin x ) c o s x d x = 2 . Tích phân ∫ 0 3 f ( x ) d x bằng
A. 8
B. 4
C. 6
D. 10
Tính nguyên hàm các hàm số sau:
1. \(I=\int\dfrac{cos^2x}{sin^8x}dx\)
2. \(I=\int\left(e^{sinx}+cosx\right)cosxdx\)
1.
\(I=\int\dfrac{cot^2x}{sin^6x}dx=\int\dfrac{cot^2x}{sin^4x}.\dfrac{1}{sin^2x}=\int cot^2x\left(1+cot^2x\right)^2.\dfrac{1}{sin^2x}dx\)
Đặt \(u=cotx\Rightarrow du=-\dfrac{1}{sin^2x}dx\)
\(I=-\int u^2\left(1+u^2\right)^2du=-\int\left(u^6+2u^4+u^2\right)du\)
\(=-\dfrac{1}{7}u^7+\dfrac{2}{5}u^5+\dfrac{1}{3}u^3+C\)
\(=-\dfrac{1}{7}cot^7x+\dfrac{2}{5}cot^5x+\dfrac{1}{3}cot^3x+C\)
Đúng 1
Bình luận (0)
2.
\(I=\int\left(e^{sinx}+cosx\right).cosxdx=\int e^{sinx}.cosxdx+\int cos^2xdx\)
\(=\int e^{sinx}.d\left(sinx\right)+\dfrac{1}{2}\int\left(1+cos2x\right)dx\)
\(=e^{sinx}+\dfrac{1}{2}x+\dfrac{1}{4}sin2x+C\)
Đúng 1
Bình luận (0)
Cho
∫
a
b
x
.
cos
x
x
.
sin
x
+
cos
x
d
x
m
Tính
∫
a
b...
Đọc tiếp
Cho ∫ a b x . cos x x . sin x + cos x d x = m Tính ∫ a b x . sin x + ( x + 1 ) cos x x . sin x + cos x d x
A. I = a+b+m
B. I = a-b+m
C. I = a+b-m
D. I = b-a+m
Tính các tích phân sau:
∫
0
π
4
x
sin
x
+
(
x
+
1
)
cos
x
xsinx
+
cosx...
Đọc tiếp
Tính các tích phân sau: ∫ 0 π 4 x sin x + ( x + 1 ) cos x xsinx + cosx d x
Tìm
F
x
∫
e
x
+
cos
x
d
x
A.
F
x
e
x
+
sin
x
+
C
B.
F
x
x...
Đọc tiếp
Tìm F x = ∫ e x + cos x d x
A. F x = e x + sin x + C
B. F x = x e x + sin x + C
C. F x = e x - sin x + C
D. F x = e x x - sin x + C
Cho hàm số
y
f
(
x
)
π
x
2
+
3
khi
x
≥
1
5
-
x...
Đọc tiếp
Cho hàm số y = f ( x ) = π x 2 + 3 khi x ≥ 1 5 - x khi x < 1 . Tính I = 2 ∫ 0 π 2 f ( sin x ) cos x d x + 3 ∫ 0 1 f ( 3 - 2 x ) d x
A. I= 32 3
B. I=31
C. 71 6
D. 32
Tìm họ nguyên hàm của hàm số sau
J
∫
cos
x
d
x
(
sin
x
+
2
cos
x
)
3
A.
J...
Đọc tiếp
Tìm họ nguyên hàm của hàm số sau J = ∫ cos x d x ( sin x + 2 cos x ) 3
A. J = 1 2 1 ( tan x + 2 ) 2 + C
B. J = - 1 2 1 ( tan x + 2 ) 2 + C
C. J = - 1 ( tan x + 2 ) 2 + C
D. J = - 1 2 1 ( tan 2 x + 2 ) 2 + C
Chọn B
I = ∫ cos x d x cos 3 x ( tan x + 2 ) 3 = ∫ d x cos 2 x ( tan x + 2 ) 3
Đặt t = tan x ⇒ d t = 1 cos 2 x d x
Do đó J = - 1 2 1 ( tan x + 2 ) 2 + C
Đúng 0
Bình luận (0)
\( \)Cho hàm số
\( f(x)=\begin{cases}x^2-1&\text{khi }x\geq2\\ x^2-2x+3&\text{khi }x<2\end{cases} \)
Tích phân 0ʃπ/2 f(2sinx + 1 )cosxdx bằng ?
Đặt \(I=\dfrac{1}{2}\int\limits^{\dfrac{\pi}{2}}_0f\left(2sinx+1\right)d\left(2sinx+1\right)\)
Đặt \(2sinx+1=t\Rightarrow I=\dfrac{1}{2}\int\limits^3_1f\left(t\right)sint=\dfrac{1}{2}\int\limits^2_1f\left(t\right)dt+\dfrac{1}{2}\int\limits^3_2f\left(t\right)dt\)
\(=\dfrac{1}{2}\int\limits^2_1\left(t^2-2t+3\right)dt+\dfrac{1}{2}\int\limits^3_2\left(t^2-1\right)dt=\dfrac{23}{6}\)
Đúng 1
Bình luận (0)
Bài tập 2: a, Tìm giá trị lớn nhất, giá trị nhỏ nhất f = \(3-\dfrac{10}{x+3}\) / [-2 : 5]
b, Tính I = \(\int\limits^{\pi}_0\left(2x-3\right)cosxdx\)
a.
\(f'\left(x\right)=\dfrac{10}{\left(x+3\right)^2}>0\Rightarrow f\left(x\right)\) đồng biến
\(\Rightarrow\min\limits_{\left[-2;5\right]}f\left(x\right)=f\left(-2\right)=-7\)
\(\max\limits_{\left[-2;5\right]}f\left(x\right)=f\left(5\right)=\dfrac{7}{4}\)
b.
Đặt \(\left\{{}\begin{matrix}u=2x-3\\dv=cosxdx\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}du=2dx\\v=sinx\end{matrix}\right.\)
\(\Rightarrow I=\left(2x-3\right)sinx|^{\pi}_0-2\int\limits^{\pi}_0sinxdx=-2\int\limits^{\pi}_0sinxdx=-4\)
Đúng 0
Bình luận (0)