Cho 2 tia đối nhau Ox và Oy ,vẽ các tia Oz, Ot nằm trên cùng 1 nửa mặt phẳng có bờ là đường thẳng xy sao cho \(\widehat{xOz}=\dfrac{1}{2}\widehat{zOy}\),\(\widehat{xOt}=2\widehat{tOy}\). Tính \(\widehat{zOt}\)
bn tự vẽ hình ik rồi mình làm cho miễn sao bn vẽ lên trên này nè tiện thể mình giảng cho lun chứ ko giảng bn thì gậy ông đập lưng ông mất
Đúng 0
Bình luận (0)
Trên nửa mặt phẳng bờ chứa tia Ox.Vẽ tia Oy và Oz sao cho widehat{xOy} 30^o,widehat{xOz}.Vẽ tia Ot trong widehat{yOz} sao cho widehat{yOt} 20^o .a)Tính widehat{yOz} .b)Tia Ot có phải là tia phân giác của widehat{yOz} không,vì sao.c)Giải thích vì sao tia Ot là tia phân giác của widehat{xOz}
Đọc tiếp
Trên nửa mặt phẳng bờ chứa tia \(O\)\(x\).Vẽ tia \(Oy\) và \(Oz\) sao cho \(\widehat{xOy}\) \(=30^o\),\(\widehat{xOz}\).Vẽ tia \(Ot\) trong \(\widehat{yOz}\) sao cho \(\widehat{yOt}\) \(=20^o\) .
a)Tính \(\widehat{yOz}\) .
b)Tia \(Ot\) có phải là tia phân giác của \(\widehat{yOz}\) không,vì sao.
c)Giải thích vì sao tia \(Ot\) là tia phân giác của \(\widehat{xOz}\)
góc xOz bao nhiêu độ vậy bạn?
Đúng 0
Bình luận (1)
Trên nửa mặt phẳng bờ tia Ox.Vẽ tia Oy và Oz sao cho widehat{xOy}30^o ,widehat{xOz}100^o.Vẽ tia Ot trong widehat{yOz} sao cho widehat{yOt}20^o.a)Tính widehat{yOz}b)Tia Ot có phải là tia phân giác của widehat{yOz} không.Vì sao?c)Giải thích vì sao tia Ot là tia phân giác của widehat{xOz}
Đọc tiếp
Trên nửa mặt phẳng bờ tia \(O\)\(x\).Vẽ tia \(Oy\) và \(Oz\) sao cho \(\widehat{xOy}\)\(=30^o\) ,\(\widehat{xOz}\)\(=100^o\).Vẽ tia \(Ot\) trong \(\widehat{yOz}\) sao cho \(\widehat{yOt}\)\(=20^o\).
a)Tính \(\widehat{yOz}\)
b)Tia \(Ot\) có phải là tia phân giác của \(\widehat{yOz}\) không.Vì sao?
c)Giải thích vì sao tia \(Ot\) là tia phân giác của \(\widehat{xOz}\)
Cho hai tia Ox,Oy đối nhau . Trên cùng nửa mặt phẳng có bờ chứa tia Ox . Vẽ các tia Oz,Ot sao cho widehat{xOz} 30o ; widehat{yOt} 75o .a) Tính widehat{zOt} b) Tính widehat{zOt} nếu widehat{xOz} a , widehat{yOt} b ( a+b ne 180o )
Đọc tiếp
Cho hai tia Ox,Oy đối nhau . Trên cùng nửa mặt phẳng có bờ chứa tia Ox . Vẽ các tia Oz,Ot sao cho \(\widehat{xOz}\) = 30o ; \(\widehat{yOt}\) = 75o .
a) Tính \(\widehat{zOt}\)
b) Tính \(\widehat{zOt}\) nếu \(\widehat{xOz}\) = a , \(\widehat{yOt}\) = b ( a+b \(\ne\) 180o )
Trên nửa mặt phẳng bờ tia chứ tia Ox.Vẽ tia Oyvà Ozsao cho widehat{xOy}30^o ,widehat{xOz}100^o.Vẽ tia Ot trong widehat{yOz} sao cho widehat{yOt}20^o.a)Tính widehat{yOz}b)Tia Ot có phải là tia phân giác của widehat{yOz} không.Vì sao?c)Giải thích vì sao tia Ot là tia phân giác của widehat{xOz}
Đọc tiếp
Trên nửa mặt phẳng bờ tia chứ tia \(O\)\(x\).Vẽ tia \(Oy\)và \(Oz\)sao cho \(\widehat{xOy}\)\(=30^o\) ,\(\widehat{xOz}\)\(=100^o\).Vẽ tia \(Ot\) trong \(\widehat{yOz}\) sao cho \(\widehat{yOt}\)\(=20^o\).
a)Tính \(\widehat{yOz}\)
b)Tia \(Ot\) có phải là tia phân giác của \(\widehat{yOz}\) không.Vì sao?
c)Giải thích vì sao tia \(Ot\) là tia phân giác của \(\widehat{xOz}\)
a)
vì \(\widehat{xoy}< \widehat{xoz}\left(30^o< 100^o\right)\) nên tia Oy nằm giữ 2 tia Ox và Oz, ta có :
\(\widehat{xoz}=\widehat{xoy}+\widehat{yoz}\)
\(\Rightarrow\widehat{yoz}=\widehat{xoz}-\widehat{xoy}=100^o-30^o=70^o\)
vậy \(\widehat{yoz}=70^o\)
b)
ta có tia ot nằm giữa 2 tia Oy và Oz nên ta có :
\(\widehat{yoz}=\widehat{yot}+\widehat{toz}\)
\(\Rightarrow\widehat{toz}=\widehat{yoz}-\widehat{yot}=70^o-20^o=50^o\)
ta có Ot nằm giữa 2 tia Oy và Oz
vì \(\widehat{toz}=50^o\) nên \(\widehat{toz}\ne\widehat{yot}\left(50^o\ne70^o\right)\) ⇒ tia ot không phải là phân giác của \(\widehat{yoz}\)
c)
ta có tia Ot nằm giữa 2 tia Ox và Oz nên
\(\widehat{xoz}=\widehat{xot}+\widehat{toz}\)
\(\Rightarrow\widehat{xot}=\widehat{xoz}-\widehat{toz}=100^o-50^o=50^o\)
vì tia Ot nằm giữa 2 tia Ox và Oz
và \(\widehat{xot}=\widehat{toz}\left(=50^o\right)\) nên tia Ot là phân giác của \(\widehat{xoz}\)
Đúng 3
Bình luận (0)
a) Trên cùng một nửa mặt phẳng bờ chứa tia Ox, ta có: \(\widehat{xOy}< \widehat{xOz}\left(30^0< 100^0\right)\)
nên tia Oy nằm giữa hai tia Ox và Oz
\(\Leftrightarrow\widehat{xOy}+\widehat{yOz}=\widehat{xOz}\)
\(\Leftrightarrow\widehat{yOz}+30^0=100^0\)
hay \(\widehat{yOz}=70^0\)
Vậy: \(\widehat{yOz}=70^0\)
Đúng 2
Bình luận (1)
+)Trên nửa mặt phẳng bờ chứa tia Ox có:∠xOy<∠xOz(30o<100o)
=>Oy là tia phân giác của Ox và Oz
+)Oy là tia phân giác của Ox và Oz
=>∠xOy+∠yOz=∠xOz
=>30o+∠yOz=100o
=>∠yOz=100o-30o=70o
Vậy ∠yOz=70o
b)+)Trên nửa mặt phẳng bờ chứa tia Oy có:∠yOt<∠yOz(20o<70o)
=>Ot nằm giữa 2 tia Oy và Oz
+)Ot nằm giữa 2 tia Oy và Oz
=>∠yOt+∠tOz=∠yOz
=>20o+∠tOz=70o
=>∠tOz=70o-20o=50o
=>∠tOz\(\ne\)∠tOy
=>Ot không phải tia phân giác của ∠yOz
c)+)Oy nằm giữa 2 tia Ox và Oz
Ot nằm giữa 2 tia Oy và Oz
=>Oy nằm giữa 2 tia Ot và Ox
+)Oy nằm giữa 2 tia Ot và Ox
=>∠xOy+∠yOt=∠xOt
=>30o+20o=∠xOt
=>50o=∠xOt
+)Ta có:∠xOt=∠tOz(=50o)(1)
+)Ot nằm giữa 2 tia Oy và Oz
Oy nằm giữa 2 tia Ox và Oz
=>Ot nằm giữa 2 tia Ox và Oz(2)
+)Từ (1) và (2)
=>Ot là tia phân giác của ∠xOz
Chúc bn học tốt
Đúng 1
Bình luận (1)
Cho 2 tia đối nhau Ox và Oy ,vẽ các tia Oz, Ot nằm trên cùng 1 nửa mặt phẳng có bờ là đường thẳng xy sao cho \(\widehat{xOz}=\dfrac{1}{2}\widehat{zOy}\),\(\widehat{xOt}=2\widehat{tOy}\). Tính \(\widehat{zOt}\)
Vì hai tia Ox, Oy đối nhau.
\(\Rightarrow\widehat{xOy}=180^o\)
Ta có: \(\widehat{xOz}\) và \(\widehat{zOy}\) kề bù.
\(\Rightarrow\widehat{xOz}+\widehat{zOy}=180^o\) (1)
Mà \(\widehat{xOz}=\dfrac{1}{2}\widehat{zOy}\) (2)
Từ (1) và (2) suy ra:
\(\dfrac{1}{2}\widehat{zOy}+\widehat{zOy}=180^o\)
\(\dfrac{3}{2}\widehat{zOy}=180^o\)
\(\widehat{zOy}=120^o\)
\(\Rightarrow\widehat{xOz}=60^o\)
Ta có: \(\widehat{xOt}\) và \(\widehat{tOy}\) kề bù.
\(\Rightarrow\widehat{xOt}+\widehat{tOy}=180^o\) (1)
Mà \(\widehat{xOt}=2\widehat{tOy}\) (2)
Từ (1) và (2) suy ra:
\(2\widehat{tOy}+\widehat{tOy}=180^o\)
\(3\widehat{tOy}=180^o\)
\(\widehat{tOy}=60^o\)
\(\Rightarrow\widehat{xOt}=120^o\)
Trên nửa mặt phằng bờ Ox, có \(\widehat{xOz}< \widehat{xOt}\left(60^o< 120^o\right)\).
\(\Rightarrow\) Tia Oz nàm giữa hai tia Ox, Ot.
\(\Rightarrow\widehat{xOz}+\widehat{zOt}=\widehat{xOt}\)
\(60^o+\widehat{zOt}=120^o\)
\(\widehat{zOt}=60^o\)
Vậy \(\widehat{zOt}=60^o\).
Đúng 0
Bình luận (0)
Trên cùng 1 nửa mặt phẳng bờ chứa tia Ox vẽ 3 tia Oy, Oz, Ot sao cho \(\widehat{xOy}=30^o,\widehat{xOz}=70^o,\widehat{xOt}=110^o\)
a) Tính số đo \(\widehat{yOz}\) và \(\widehat{zOt}\)
b) Trong 3 tia Oy, Oz, Ot tia nào nằm giữa tia còn lại? Vì sao
c) Chứng minh: Oz là tia phân giác của \(\widehat{yOt}\)

a) Vì \(\widehat{xOy}< \widehat{xOz}\left(30^o< 70^o\right)\)
\(\Rightarrow\) Tia Oy nằm giữa 2 tia Ox và Oz
\(\Rightarrow\widehat{yOz}=70^o-30^o=40^o\)
Vì \(\widehat{xOz}< \widehat{xOt}\left(70^o< 110^o\right)\)
\(\Rightarrow\) Tia Oz nằm giữa 2 tia Ox và Ot
\(\Rightarrow\widehat{zOt}=110^o-70^o=40^o\)
b) Vì \(\widehat{xOy}< \widehat{xOt}\left(30^o< 110^o\right)\)
\(\Rightarrow\) Tia Oy nằm giữa 2 tia Ox và Ot
\(\Rightarrow\widehat{yOt}=110^o-30^o=80^o\)
Theo a, ta có:
\(\widehat{yOz}=40^o\\ \Rightarrow\widehat{yOz}< \widehat{yOt}\left(40^o< 80^o\right)\)
\(\Rightarrow\) Tia Oz nằm giữa 2 tia Oy và Ot
c) Theo b, Tia Oz nằm giữa 2 tia Oy và Ot và có:
\(\widehat{yOz}=40^o,\widehat{zOt}=40^o\)
\(\Rightarrow\) Oz là tia phân giác của \(\widehat{yOt}\)
Trên cùng một nửa mặt phẳng bờ chứa tia Ox vẽ 2 tia Ot và Oy sao cho widehat{xOt}30^o,widehat{xOy}60^o.a)Tia Ot có nằm giữa 2 tia còn lại không b)So sánh widehat{tOy} và widehat{xOt}c)tia Ot có là tia phân giác của widehat{xOy} không,vì sao.
Đọc tiếp
Trên cùng một nửa mặt phẳng bờ chứa tia \(O\)\(x\) vẽ 2 tia \(Ot\) và \(Oy\) sao cho \(\widehat{xOt}\)\(=30^o\),\(\widehat{xOy}\)\(=60^o\).
a)Tia \(Ot\) có nằm giữa 2 tia còn lại không
b)So sánh \(\widehat{tOy}\) và \(\widehat{xOt}\)
c)tia \(Ot\) có là tia phân giác của \(\widehat{xOy}\) không,vì sao.
Vì xOt = 30 , xOy = 60
=> xOt < xOy Mà Ot, Oy cùng nằm trên nửa mặt phẳng bờ Ox
=> Ot nằm giữa Ox và Oy.
Vì Ot nằm giữa Ox và Oy
=> tOx + tOy = xOy
=> 30 + tOy=60
=> tOy=30 Mà tOx=30
=> tOy= tOx
Vì tOy = tOx ; Ot nằm giữa Ox và Oy
=> Ot là tia phân giác góc xOy
Đúng 2
Bình luận (0)
a) Trên cùng một nửa mặt phẳng bờ chứa tia Ox, ta có: \(\widehat{xOt}< \widehat{xOy}\left(30^0< 60^0\right)\)
nên tia Ot nằm giữa hai tia Ox và Oy
Đúng 1
Bình luận (0)
a) tia Ot nàm giữa 2 tia còn lại vì \(\widehat{xot}< \widehat{xoy}\left(30^o< 60^o\right)\)
b)ta có tia Ot nàm giưa 2 tia Ox và Oy nên:
\(\widehat{xoy}=\widehat{xot}+\widehat{toy}\)
\(\Rightarrow\widehat{toy}=\widehat{xoy}-\widehat{xot}=60^o-30^o=30^o\)
ta có \(\widehat{xot}=30^o\) và \(\widehat{toy}=30^o\)
\(\Rightarrow\widehat{xot}=\widehat{toy}\left(30^o=30^o\right)\)
vậy \(\widehat{xot}=\widehat{toy}\)
c) Ot là phân giác của \(\widehat{xoy}\) vì :\(\widehat{toy}=\widehat{xot}\left(30^o=30^o\right)\) (theo câu a)
và Ot nàm giữa 2 tia Ox và Oy (theo câu b)
Đúng 3
Bình luận (0)
Cho đường thẳng xy đi qua điểm O. Vẽ tia Oz sao cho \(\widehat {xOz} = 135^\circ \). Vẽ tia Ot sao cho \(\widehat {yOt} = 90^\circ \) và \(\widehat {zOt} = 135^\circ \). Gọi Ov là tia phân giác của \(\widehat {xOt}\). Các góc \(\widehat {xOv}\) và \(\widehat {yOz}\) có phải là hai góc đối đỉnh không? Vì sao?
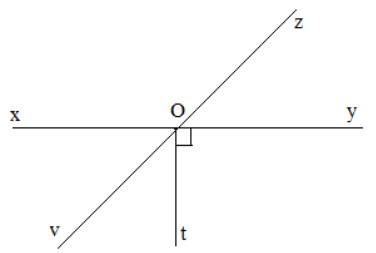
Vì \(\widehat {yOt} = 90^\circ \Rightarrow Oy \bot Ot \Rightarrow Ox \bot Ot\) nên \(\widehat {xOt} = 90^\circ \)
Vì Ov là tia phân giác của \(\widehat {xOt}\) nên \(\widehat {xOv} = \widehat {vOt} = \frac{1}{2}.\widehat {xOt} = \frac{1}{2}.90^\circ = 45^\circ \)
Vì \(\widehat {vOz} =\widehat {vOx} + \widehat {xOz} = 45^\circ + 135^\circ = 180^\circ \) nên Ov và Oz là hai tia đối nhau
Như vậy, các góc \(\widehat {xOv}\) và \(\widehat {yOz}\) là hai góc đối đỉnh vì Ox là tia đối của tia Oy, tia Ov là tia đối của tia Oz
Đúng 1
Bình luận (0)
trên 1 nửa mặt phẳng bờ chứa tia Ox vẽ Oy và Oz sao cho \(\widehat{xOy}=30^o;\widehat{xOz}=100^o\)
a) tính \(\widehat{yOz}\)
b) gọi Ot là tia phân giác của \(\widehat{xOz}\) . tính \(\widehat{tOy}\)
c) vẽ tia Oy, là tia đối của tia oy, kể tên các cặp góc kề bù
a, Ta có : \(\widehat{yOz}=\widehat{xOz}-\widehat{xOy}=100^o-30^o=70^o\)
b, Vì Ot là phân giác góc xOz nên :
\(\widehat{zOt}=\frac{1}{2}\widehat{xOz}=50^o\)
=> \(\widehat{yOt}=\widehat{yOz}-\widehat{zOt}=70^o-50^o=20^o\)
c, Các cặp góc kề bù : yOt và tOy' ; yOz và y'Oz ; xOy và xOy' .
Đúng 0
Bình luận (0)


























