Lập phương trình tính tổng :
A=1+1/2+1/3+...+1/n
Những câu hỏi liên quan
trong mp oxy, cho điểm a (1;-3). b (0,1): vectơ n= (3;1) a) lập phương trình tổng quát của đường thẳng d đi qua điểm a và có vtpt là n b) lập phương trình thăm số của đường thẳng ab c) tính khoảng cách từ điểm b đến đường thẳng d d) tính góc giữa 2 đường thẳng d và có phương trình 5x-y+1=0
a: Phương trình tổng quát là:
3(x-1)+1(y+3)=0
=>3x-3+y+3=0
=>3x+y=0
b: vecto AB=(-1;4)
Phương trình tham số của AB là:
\(\left\{{}\begin{matrix}x=1-t\\y=-3+4t\end{matrix}\right.\)
c: \(d\left(B;d\right)=\dfrac{\left|0\cdot3+1\cdot1\right|}{\sqrt{3^2+1^2}}=\dfrac{1}{\sqrt{10}}\)
Đúng 0
Bình luận (0)
Lập phương trình tổng quát của mặt phẳng (MNP) với M(1; 1; 1), N(4; 3; 2), P(5; 2; 1).
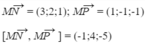
⇒ Một vecto pháp tuyến của mặt phẳng (MNP) là n → (1;-4;5)
Phương trình tổng quát của mặt phẳng (MNP) với M(1; 1; 1), N(4; 3; 2), P(5; 2; 1)là : (x-1)-4(y-1)+5(z-1)=0
Hay x - 4y + 5z - 2 = 0
Đúng 0
Bình luận (0)
cho ∆ABC có A(1;5), B(0;3), C(-2;-1) a, lập phương trình tham số AB,BC,AC b, lập phương trình tổng quát của trung tuyến AM c, lập phương trình tổng quát của BC d, tính khoảng cách từ A đến BC
a: vecto AB=(-1;-2)
Phương trình tham số của AB là:
\(\left\{{}\begin{matrix}x=1-t\\y=5-2t\end{matrix}\right.\)
vecto AC=(-3;-6)=(-1;-2)=(1;2)
Phương trình tham số của AC là:
\(\left\{{}\begin{matrix}x=1+t\\y=5+2t\end{matrix}\right.\)
vecto BC=(-2;-4)=(1;2)
Phương trình tham số của BC là:
\(\left\{{}\begin{matrix}x=0+t=t\\y=2+3t\end{matrix}\right.\)
c: vetco BC=(1;2)
=>VTPT là (-2;1)
Phương trình BC là:
-2(x+2)+1(y+1)=0
=>-2x-4+y+1=0
=>-2x+y-3=0
=>2x-y+3=0
b: Tọa độ M là:
x=(0-2)/2=-1 và y=(3-1)/2=1
M(-1;1); A(1;5)
vecto AM=(-2;-4)=(1;2)
=>VTPT là (-2;1)
Phương trình AM là:
-2(x+1)+1(y-1)=0
=>-2x-2+y-1=0
=>-2x+y-3=0
=>2x-y+3=0
d: \(d\left(A;BC\right)=\dfrac{\left|1\cdot2+5\cdot\left(-1\right)+3\right|}{\sqrt{2^2+1^2}}=0\)
Đúng 1
Bình luận (0)
Cứu tớ với ạ
Câu 2 là 1 phần 2, 1 phần 3, 1 phần 20 í ạ không phải chia đâu ạ
Câu 1: Lập trình tổng: A=1+2+3+...+n Ở đây n là số tự nhiên được nhập từ bàn phím. ( Viết bằng lệch for...to...do)
Câu 2: Lập trình tính tổng nghịch đảo của 20 số tự nhiên đầu tiên 1+1/2+1/3+...1/20
Câu 1:
uses crt;
var i,n,t:integer;
begin
clrscr;
readln(n);
t:=0;
for i:=1 to n do
t:=t+i;
writeln(t);
readln;
end.
Đúng 0
Bình luận (0)
Cho số tự nhiên n Hãy lập trình tính tổng sau s =1+1/2+1/3+...+1/n
Tham khảo:
Uses Crt ;
Var i , n : Integer ;
tong: Real ;
BEGIN
Clrscr ;
Write (‘ Cho so tu nhien n : ‘) ; Readln (n) ;
tong :=0 ;
i :=1 ;
While i <= n Do
Begin
tong := tong + 1/i ;
i := i + 1 ;
End ;
Writeln (‘ Tong can tim la : ‘, tong:12:6 ) ;
Readln ;
END .
Đúng 0
Bình luận (0)
Cho số tự nhiên n Hãy lập trình tính tổng sau
S= 1+1/2+1/3+...+1/n
Xem chi tiết
Cho tam giác ABC biết A(1; 4), B(3; -1) và C(6; 2).
a, Lập phương trình tổng quát của các đường thẳng AB, BC và CA.
b, Lập phương trình tổng quát của đường cao AH và trung tuyến AM.
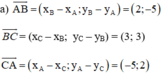
+ Lập phương trình đường thẳng AB:
Đường thẳng AB nhận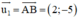 
là 1 vtcp ⇒ AB nhận 
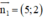là 1 vtpt
Mà A(1; 4) thuộc AB
⇒ PT đường thẳng AB: 5(x- 1) + 2(y – 4) = 0 hay 5x + 2y – 13 = 0.
+ Lập phương trình đường thẳng BC:
Đường thẳng BC nhận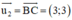 
là 1 vtcp ⇒ BC nhận 
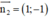là 1 vtpt
Mà B(3; –1) thuộc BC
⇒ Phương trình đường thẳng BC: 1(x - 3) – 1(y + 1) = 0 hay x – y – 4 = 0.
+ Lập phương trình đường thẳng CA:
Đường thẳng CA nhận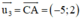 
là 1 vtcp ⇒ CA nhận 
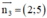là 1 vtpt
Mà C(6; 2) thuộc CA
⇒ Phương trình đường thẳng AC: 2(x – 6) + 5(y - 2) = 0 hay 2x + 5y – 22 = 0.
b) + AH là đường cao của tam giác ABC ⇒ AH ⊥ BC
⇒ Đường thẳng AH nhận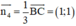 
là 1 vec tơ pháp tuyến
Mà A(1; 4) thuộc AH
⇒ Phương trình đường thẳng AH: 1(x - 1) + 1(y - 4) = 0 hay x + y – 5 = 0.
+ Trung điểm M của BC có tọa độ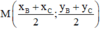 
hay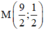 
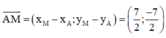
Đường thẳng AM nhận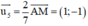 
là 1 vtcp
⇒ AM nhận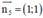 
là 1 vtpt
Mà A(1; 4) thuộc AM
⇒ Phương trình đường thẳng AM: 1(x - 1) + 1(y – 4) = 0 hay x + y – 5 = 0.
Đúng 1
Bình luận (0)
Không giải phương trình \(x^2-11x+5=0\) (1)
a, Tính tổng bình phương các nghiệm của phương trình (1)
b, Lập phương trình bậc 2 có nghiệm là nghịch đảo các nghiệm của phương trình (1)
giúp 2 câu này với:
1/Giải phương trình: (x2-20162)2-8064x-1
2/CM trong 4 số tn liên tiếp, tổng của lập phương ba số đầu bằng lập phương số thứ tư: n3+(n+1)3+(n+2)3=(n+3)3
Trong mặt phẳng toạ độ, chovec n left( {2;{rm{ }}1} right),{rm{ }}vec v{rm{ }} {rm{ }}left( {3,{rm{ }}2} right),{rm{ }}Aleft( {1,{rm{ }}3} right),{rm{ }}Bleft( { - 2;{rm{ }}1} right) .a) Lập phương trình tổng quát của đường thẳng {Delta _1} đi qua A và có vectơ pháp tuyến overrightarrow n .b) Lập phương trình tham số của đường thẳng {Delta _2}, đi qua B và có vectơ chỉ phương overrightarrow v .c) Lập phương trình tham số của đường thẳng AB.
Đọc tiếp
Trong mặt phẳng toạ độ, cho\(\vec n = \left( {2;{\rm{ }}1} \right),{\rm{ }}\vec v{\rm{ }} = {\rm{ }}\left( {3,{\rm{ }}2} \right),{\rm{ }}A\left( {1,{\rm{ }}3} \right),{\rm{ }}B\left( { - 2;{\rm{ }}1} \right)\) .
a) Lập phương trình tổng quát của đường thẳng \({\Delta _1}\) đi qua A và có vectơ pháp tuyến \(\overrightarrow n \).
b) Lập phương trình tham số của đường thẳng \({\Delta _2}\), đi qua B và có vectơ chỉ phương \(\overrightarrow v \).
c) Lập phương trình tham số của đường thẳng AB.
a) Phương trình tổng quát của đường thẳng \({\Delta _1}\) là: \(2\left( {x - 1} \right) + 1\left( {y - 3} \right) = 0 \Leftrightarrow 2x + y - 5 = 0\).
b) Phương trình tham số của đường thẳng \({\Delta _2}\) là:\(\left\{ \begin{array}{l}x = - 2 + 3t\\y = 1 + 2t\end{array} \right.\)
c) Phương trình đường thẳng AB đi qua điểm \(A\left( {1;3} \right)\) nhận \(\overrightarrow {AB} = \left( { - 3; - 2} \right)\) là vectơ chỉ phương nên phương trình tham số của AB là \(\left\{ \begin{array}{l}x = 1 - 3t\\y = 3 - 2t\end{array} \right.\)
Đúng 0
Bình luận (0)