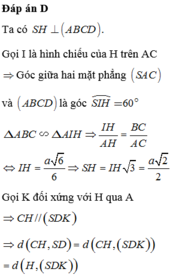Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật ,AB=a,AD=a√3 , mp(SAB)vuông góc với đáy và tam giác SAB cân tại S , I là trung điểm AB , K là trung điểm CD góc giữa SB và mp đáy là 45 độ . a) chứng minh SI vuông vs (ABCD) b)chứng minh rằng (SIK)vuông (SCD) c) tính góc giữa SC và (SAB)

Những câu hỏi liên quan
Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật ,AB=a,AD=a√3 , mp(SAB)vuông góc với đáy và tam giác SAB cân tại S , I là trung điểm AB , K là trung điểm CD góc giữa SB và mp đáy là 45 độ . a) chứng minh SI vuông vs (ABCD) b)chứng minh rằng (SIK)vuông (SCD) c) tính góc giữa SC và (SAB)
a: (SAB) vuông góc (ABCD)
(SAB) giao (ABCD)=AB
SI vuông góc AB
=>SI vuông góc (ABCD)
b: CD vuông góc SI
CD vuông góc IK
=>CD vuông góc (SIK)
=>(SCD) vuông góc (SIK)
Đúng 0
Bình luận (0)
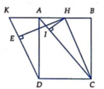
Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật, mặt phẳng (SAB) vuông góc với mặt đáy, tam giác SAB vuông cân tại S. Gọi M là trung điểm của AB. Chứng minh rằng:
a) SM⊥(ABCD);
b) AD⊥(SAB);
c) (SAD)⊥(SBC).
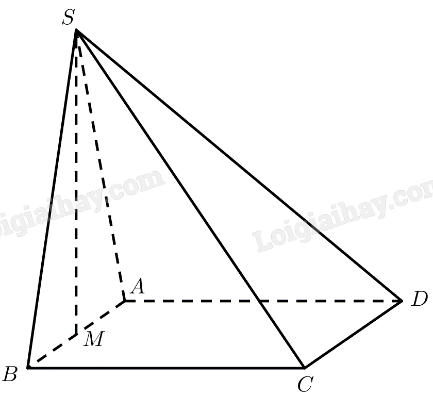
a, Tam giác \(SAB\) vuông cân tại \(S\), có \(M\) là trung điểm của \(AB\)
\(\left. \begin{array}{l} \Rightarrow SM \bot AB\\\left( {SAB} \right) \bot \left( {ABCD} \right)\\\left( {SAB} \right) \cap \left( {ABCD} \right) = AB\end{array} \right\} \Rightarrow SM \bot \left( {ABCD} \right)\)
b) \(ABCD\) là hình chữ nhật \( \Rightarrow AB \bot A{\rm{D}}\)
\(SM \bot \left( {ABCD} \right) \Rightarrow SM \bot A{\rm{D}}\)
\( \Rightarrow A{\rm{D}} \bot \left( {SAB} \right)\)
c) \(A{\rm{D}} \bot \left( {SAB} \right) \Rightarrow A{\rm{D}} \bot SB\)
Tam giác \(SAB\) vuông cân tại \(S\)\( \Rightarrow SA \bot SB\)
\(\left. \begin{array}{l} \Rightarrow SB \bot \left( {SA{\rm{D}}} \right)\\SB \subset \left( {SBC} \right)\end{array} \right\} \Rightarrow \left( {SBC} \right) \bot \left( {SA{\rm{D}}} \right)\)
Tam giác \(SAB\) vuông cân tại \(S\), có \(M\) là trung điểm của \(AB\)
\(\left. \begin{array}{l} \Rightarrow SM \bot AB\\\left( {SAB} \right) \bot \left( {ABCD} \right)\\\left( {SAB} \right) \cap \left( {ABCD} \right) = AB\end{array} \right\} \Rightarrow SM \bot \left( {ABCD} \right)\)
b) \(ABCD\) là hình chữ nhật \( \Rightarrow AB \bot A{\rm{D}}\)
\(SM \bot \left( {ABCD} \right) \Rightarrow SM \bot A{\rm{D}}\)
\( \Rightarrow A{\rm{D}} \bot \left( {SAB} \right)\)
c) \(A{\rm{D}} \bot \left( {SAB} \right) \Rightarrow A{\rm{D}} \bot SB\)
Tam giác \(SAB\) vuông cân tại \(S\)\( \Rightarrow SA \bot SB\)
\(\left. \begin{array}{l} \Rightarrow SB \bot \left( {SA{\rm{D}}} \right)\\SB \subset \left( {SBC} \right)\end{array} \right\} \Rightarrow \left( {SBC} \right) \bot \left( {SA{\rm{D}}} \right)\)
Đúng 0
Bình luận (0)
Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật với
A
B
a
,
A
D
a
2
. Gọi H là trung điểm của cạnh AB. Tam giác SAB cân tại S và nằm trong mặt phẳng vuông góc với đáy. Góc giữa hai mặt phẳng (SAC) và (ABCD) là
60
°
. Tính khoảng cách giữa hai đường thẳng CH và SD A.
2
a
5...
Đọc tiếp
Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật với A B = a , A D = a 2 . Gọi H là trung điểm của cạnh AB. Tam giác SAB cân tại S và nằm trong mặt phẳng vuông góc với đáy. Góc giữa hai mặt phẳng (SAC) và (ABCD) là 60 ° . Tính khoảng cách giữa hai đường thẳng CH và SD
A. 2 a 5 5
B. 2 a 10 5
C. a 5 5
D. 2 a 2 5
Cho hình chóp S.ABCD có đáy ABCD là hình thang vuông tại A và D, SA=AD=DC=a, AB=2a; SA vuông góc voi đáy. E trung điểm AB.
a) chứng minh các mặt bên chóp là tam giác vuông
b) tính góc giữa (SBC) và (ABCD); SC và (SAB)
c) tính khoảng cách từ A đến mp(SBC) và khoảng cách giữa 2 đt SC và AC?
Bạn kiểm tra lại đề,
1. ABCD là hình thang vuông tại A và B hay A và D? Theo dữ liệu này thì ko thể vuông tại B được (cạnh huyền DC nhỏ hơn cạnh góc vuông AB là cực kì vô lý)
2. SC và AC cắt nhau tại C nên giữa chúng không có khoảng cách. (khoảng cách bằng 0)
Đúng 0
Bình luận (1)
Hình chóp S.ABCD, ABCD là hình vuông và tam giác SAB đều cạnh a. I là trung điểm AB. SI vuông góc với đáy. Tính góc giữa SC và mp(SAD)
Trong mp(SAD) kẻ DF//SA
SA⊥AD => DF⊥AD mà AD⊥DC => AD⊥(DCF)
Kẻ CH⊥DF => CH⊥AD => CH⊥(SAD)
=> H là hình chiếu của C lên (SAD)
=> \(\widehat{\left(SC,\left(SAD\right)\right)}=\widehat{\left(SC,SH\right)}=\widehat{CSH}\)
ΔCFD=ΔSAB => ΔCFD đều cạnh a => CH= \(\dfrac{\sqrt{3}}{2}a\)
SC= \(\sqrt{2}a\)
Xét tam giác SCH vuông ở H ta có:
sin CSH= \(\dfrac{HC}{SC}\)=\(\dfrac{\sqrt{6}}{4}\)
=> \(\widehat{CSH}\)= arcsin\(\dfrac{\sqrt{6}}{4}\)
Đúng 0
Bình luận (0)
Cho hình chóp S.ABCD, đáy ABCD là hình thang vuông tại A và D. SA=a căn (3), AB=2a, AD=DC=a. Gọi I là trung điểm AB a. Tính góc giữa mp (SDC) và mp (ABCD) b. Tính góc giữa mp (SDI) và mp (ABCD) c. CM (SCI) vuông góc với (SAB) d. CM (SBC) vuông góc với (SAC)
Đề bài thiếu chi tiết định dạng điểm S nên không giải được (ví dụ phải thêm SA vuông góc mặt đáy hoặc gì đó tương tự)
Đúng 0
Bình luận (1)
Cho hình chóp S.ABCD có đáy là hình chữ nhật,
A
B
a
,
A
D
2
a
.
Tam giác SAB cân tại S và nằm trong mặt phẳng vuông góc với đáy. Góc giữa đường thẳng SC và mặt phẳng (ABCD) bằng
45
°
.Gọi M là trung điểm của SD. Tính theo a khoảng cách d từ điểm M đến mặt phẳng (SAC). A.
d
a
1315...
Đọc tiếp
Cho hình chóp S.ABCD có đáy là hình chữ nhật, A B = a , A D = 2 a . Tam giác SAB cân tại S và nằm trong mặt phẳng vuông góc với đáy. Góc giữa đường thẳng SC và mặt phẳng (ABCD) bằng 45 ° .Gọi M là trung điểm của SD. Tính theo a khoảng cách d từ điểm M đến mặt phẳng (SAC).
A. d = a 1315 89
B. d = a 1513 89
C. d = 2 a 1315 89
D. d = 2 a 1513 89
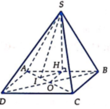
Đáp án B
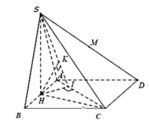
Dễ thấy: S C H ^ = 45 ∘ Gọi H là trung điểm của AB ta có S H ⊥ A B ⇒ S H ⊥ A B C D .
Ta có: S H = H C = a 17 2 .
Ta có: d = d M , S A C = 1 2 d D , S A C
Mà 1 2 d D , S A C = 1 2 d B , S A C nên d = d H , S A C
Kẻ H I ⊥ A C , H K ⊥ S I ⇒ d H , S A C = H K
Ta có: H I = A B . A D 2 A C = a 5 5
Từ đó suy ra: d = H K = S H . H I S I = a 1513 89 .
Đúng 0
Bình luận (0)
Cho hình chóp S.ABCD có đáy là hình chữ nhật với AB2a, ADa. Tam giác SAB là tam giác cân tại S và nằm trong mặt phẳng vuông góc với đáy. Góc giữa mặt phẳng (SBC) và (ABCD) bằng
45
°
. Khi đó thể tích khối chóp S.ABCD là A.
2
a
3
B.
2
3
a
3
C.
3...
Đọc tiếp
Cho hình chóp S.ABCD có đáy là hình chữ nhật với AB=2a, AD=a. Tam giác SAB là tam giác cân tại S và nằm trong mặt phẳng vuông góc với đáy. Góc giữa mặt phẳng (SBC) và (ABCD) bằng 45 ° . Khi đó thể tích khối chóp S.ABCD là
A. 2 a 3
B. 2 3 a 3
C. 3 3 a 3
D. 1 3 a 3
Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật,
A
B
a
,
A
D
2
a
góc giữa hai mặt phẳng (SAC) và (ABCD) bằng 60°. Gọi H là trung điểm của AB. Biết rằng tam giác SAB cân tại S và nằm trong mặt phẳng vuông góc với đáy. Tính theo a bán kính mặt cầu ngoại tiếp hình chóp S.HAC. A.
9
2
a
8
B....
Đọc tiếp
Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật, A B = a , A D = 2 a góc giữa hai mặt phẳng (SAC) và (ABCD) bằng 60°. Gọi H là trung điểm của AB. Biết rằng tam giác SAB cân tại S và nằm trong mặt phẳng vuông góc với đáy. Tính theo a bán kính mặt cầu ngoại tiếp hình chóp S.HAC.
A. 9 2 a 8
B. 62 a 16
C. 62 a 8
D. 31 a 32
Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật biết AB=a; AD= 2a; SA vuông góc với đáy, SA=a√2. Xác định và tính góc giữa. a) Các đường thẳng SB, SC, SD với mp đáy. b) SC với các mp (SAD) và ( SAB). c) SA với mp (SCD). d) SB và (SAC).