\(A+A_1+B+B_1+C+C_1=3.180\)

Mà A+B+C=180=> \(A_1+B_1+C_1=360\)

Câu hỏi tương tự nha ! Kéo xuống là thấy !!! 

tích nha

vì một góc ngoài bằng tổng 2 góc trong cộng lại thì 3 góc ngoài nhân lên bằng 360⁰(tick nha) 

Gọi A^1, B^1, C^1 là 3 góc trong của tam giác ABC. A^2, B^2,C^2 là 3 góc ngoài của tam giác ABC.
Ta có:
A^1 + A^2 = 180⁰
B^1 + B^2 = 180⁰
C^1 + C^2 = 180⁰
---------------------
Cộng vế theo vế được:
A^1 +B^1 +C^1 +A^2 +B^2 +C^2 = 3.180⁰
mà A^1 +B^1 +C^1 = 180⁰ (tổng 3 góc trong của tam giác)
=> A^2 +B^2 +C^2 = 3.180⁰ - 180⁰ = 2.180⁰ = 360⁰

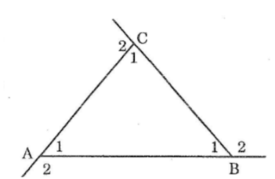
Ta có: ∠(A1 ) +∠(A2 ) =180o(hai góc kề bù)

∠(B1 ) +∠(B2 ) =180o(hai góc kề bù)

∠(C1 ) +∠(C2 )=180o(hai góc kề bù)

Suy ra: ∠(A1 ) +∠(A2 ) +∠(B1) +∠(B2 ) +∠(C1 ) +∠(C2 ) = 180º + 180º + 180º =540o

⇒∠(A2 ) + ∠( B2 ) +∠(C2 ) =540o-(∠(A1 ) +∠(B1 ) +∠(C1 ) ) (1)

Trong ΔABC, ta có:

∠(A1 ) +∠(B1 ) +∠(C1 ) =180o (tổng ba góc trong tam giác) (2)

Từ (1) và (2) suy ra: ∠(A2 ) +∠(B2 ) +∠(C2 ) =540o-180o=360o

Gọi 3 góc ngoài ở 3 đỉnh của 1 tam giác lần lượt là A₁;B₁;C₁ còn A₂;B₂;C₂ là góc trong của tam giác.

Ta có:

A₁ + A₂ = 180^o

B₁ + B₂ = 180^o

C₁ + C₂ = 180^o

=> A₁+B₁+C₁+A₂+B₂+C₂ = 360^o

Mà A₂ + B₂ + C₂ = 180^o (tổng 3 góc trong của tam giác)

=> A₁+B₁+C₁ = 360^o-180^o=180^o.2 = 360^o

Chẳng những đối với tam giác mà đối với mọi đa giác lồi,tổng số đo các góc ngoài luôn luôn bằng 360 độ 
Ở cuối chương tứ giác (lớp 8),em sẽ học công thức tổng quát tính tổng số đo các góc trong của n-giác lồi (n>=3) là: (n-2).180độ 
Góc ngoài tại mỗi đỉnh là góc kề bù với góc trong tại đỉnh đó 
Tại n- đỉnh ta có n-góc bẹt là tổng số đo của n-góc TRONG và NGOÀI của n-giác lồi 
Vậy tổng số đo n- góc ngoài của n-giác lồi là 
n.180độ - (n-2).180độ=2.180độ=360độ 
----------------- 

Lời giải:
Gọi $\widehat{A}, \widehat{B}, \widehat{C}$ là 3 góc trong tam giác $ABC$ và $\widehat{A_1}, \widehat{B_1}, \widehat{C_1}$ tương ứng là 3 góc ngoài 3 đỉnh.

Ta có:

$\widehat{A_1}+\widehat{B_1}+\widehat{C_1}=(180^0-\widehat{A})+(180^0-\widehat{B})+(180^0-\widehat{C})$

$=540^0-(\widehat{A}+\widehat{B}+\widehat{C})$

$=540^0-180^0=360^0$

theo tinh chat goc ngoai cua tam giac , ta lan luo co :

goc ngoai cua a=goc b+goc c

goc ngoai cua b=goc a+goc c

goc ngoai cua c=goc a+goc b

cong theo tung ve cua cac dang thuc tren ta duoc:

goc ngoai cua a +goc ngoai cua b+goc ngoai cua c=goc b+gocc+goca+goc c+goca+goc b=2(goc a+goc b+goc c)=2.180 do =360 do 

minh lam vay chu trong bai ban ghi goc ngoai cua a la a1 ,goc ngoai cua b la b1, goc ngoai cua c=c1 nhe de cho de lam  

sai đề rồi

nhầm. Bài này dựa vào tính chất góc trong là ra mế