cho tam giác ABC có A(0;1),B (2;0),C (- 2;- 5) . Tính diện tích S của tam giác ABC

Những câu hỏi liên quan
Trong không gian Oxyz cho tam giác ABC có tọa độ các đỉnh là:
A(a; 0; 0), B(0; b; 0), C(0; 0; c)
Chứng minh rằng tam giác ABC có ba góc nhọn.
Ta có: AB → = (−a; b; 0) và AC → = (−a; 0; c)
Vì AB → . AC → = a 2 > 0 nên góc ∠ BAC là góc nhọn.
Lập luận tương tự ta chứng minh được các góc ∠ B và ∠ C cũng là góc nhọn.
Đúng 0
Bình luận (0)
Cho tam giác ABC có \(\widehat A = \)\({100^0}\),\(\widehat B\)\( = {40^o}\).
a) Tìm cạnh lớn nhất của tam giác ABC.
b) Tam giác ABC là tam giác gì? Vì sao?
a) Do \(\widehat{A}=100^0>90^0\) nên là góc tù, do đó, \(\widehat{A}\) là góc lớn nhất trong tam giác ABC.
\( \Rightarrow \) BC là cạnh lớn nhất của tam giác ABC (do BC đối diện với góc A trong tam giác ABC)
b)
Theo định lí tổng 3 góc trong tam giác ABC, ta có:
\( \Rightarrow \widehat A + \widehat B + \widehat C = {180^o}\)
\( \Rightarrow \widehat C = {180^o} - {100^o} - {40^o} = {40^o}\)
\( \Rightarrow\widehat C = \widehat B = {40^o}\)
\( \Rightarrow \) ABC là tam giác cân tại A.
Đúng 2
Bình luận (0)
BÀI TẬP
Bài 1. Cho tam giác ABC có AB=5cm; AC=7cm. So sánh <B và <C
Bài 2. Cho tam giác ABC có AB=3cm; AC= 4cm;BC = 5cm. So sánh các góc của
tam giác
Bài 3.Cho tam giác có <B=60 0 ; <C =40 0 . So sánh các cạnh của tam giác ABC
Bài 4. Cho tam giác ABC vuông ở A có AB= 6cm; BC = 10 cm
1/ Tính AC
2/ So sánh các góc của tam giác ABC
Cho tam giác ABC có A(-1;0),B(4;0),C(0;m), m≠0. Gọi G là trọng tâm của tam giác ABC. Xác định m để tam giác GAB vuông tại G
Cho tam giác ABC có A(-1;0) , B(4;0) , C(0;m) và m khác 0. Gọi G là trọng tâm của tam giác ABC. Xđ m để tam giác GAB vuông tại G
Tọa độ trọng tâm G của ΔABC là \(G\left(1;\dfrac{m}{3}\right)\)
⇒ \(\left\{{}\begin{matrix}\overrightarrow{AG}=\left(2;\dfrac{m}{3}\right)\\\overrightarrow{BG}=\left(-3;\dfrac{m}{3}\right)\end{matrix}\right.\)
Để ΔGAB vuông tại G
⇒ GA ⊥ GB
⇒ \(\overrightarrow{GA}\) ⊥ \(\overrightarrow{GB}\)
⇒ \(\overrightarrow{GA}.\overrightarrow{GB}=0\)
⇒ 2 . (-3) + \(\dfrac{m^2}{9}\) = 0
⇒ m2 = 6 . 9 = 54
⇒ m = \(\pm\sqrt{54}\)
Mình chắc chắn cách làm của mình là đúng còn về tính toán thì chưa chắc nên bạn tự kiểm tra nhá ![]()
Đúng 1
Bình luận (0)
Cho tam giác ABC có A(-1; 1), B(0; 2), C(1; 1). Trực tâm của tam giác ABC có tọa độ là
A.(0; 2)
B. (0; 1)
C. (1; 0)
D. (1; 1)
Gọi tọa độ điểm H(a;b)
Ta có: A H → = a + 1 ; b − 1 , B H → = a ; b − 2 , B C → = 1 ; − 1 , A C → 2 ; 0
Do H là trực tâm tam giác ABC nên:
A C → . B H → = 0 B C → . A H → = 0 ⇒ 2. a + 0. b − 2 = 0 1. a + 1 − 1. b − 1 = 0 ⇒ a = 0 b = 2
Vậy H (0; 2).
Chọn A
Đúng 0
Bình luận (0)
B1. Cho tam giác ABC có góc A =90, BX=a(a>0),Ab=a/2. Tính BC
B2. Tam giácgiác ABC có AB=a(a>0), BC=\(\sqrt{2}\) .a.CMR tam giác ABC vuông
cho tam giác ABC có AB= a căn 5, BC= a căn 3, AC= a căn 2( a>0)
a) tam giác ABC là tg gì
Ta có: \(AC^2+BC^2=\left(a\sqrt{2}\right)^2+\left(a\sqrt{3}\right)^2=2a^2+3a^2=5a^2\)
\(AB^2=\left(a\sqrt{5}\right)^2=5a^2\)
=> \(AB^2=AC^2+BC^2\)
=> Tam giác ABC vuông tại C (định lí Pytago đảo)
Đúng 1
Bình luận (0)
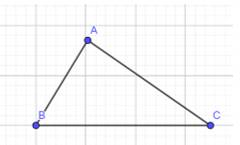
Cho tam giác ABC có A(1; -1) ; B(3; -3) và C(6; 0). Diện tích tam giác ABC là:
A. 12
B. 6
C. 6 2
D. 9
Chọn B.
Ta có:
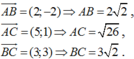
Mặt khác ![]()
Suy ra diện tích tam giác ABC là 1/2.AB.BC = 6.
Đúng 0
Bình luận (0)
Cho tam giác ABC có A( -1; 3) ; B( -2; 0) và C( 5;1). Trực tâm H của tam giác ABC có toạ độ là:
A. (3 ; -1)
B. (-1 ; 3)
C. (2 ; -1)
D. (2 ; -3)
Ta có:
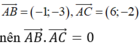
Suy ra tam giác ABC vuông tại A do đó trực tâm H trùng với A
Vậy H( -1 ; 3)
Chọn B.
Đúng 0
Bình luận (0)

















