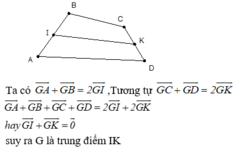
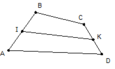
Vị trí của gd và đt

Những câu hỏi liên quan
Đề thi HSG toán 6 phòng GD&ĐT Hoằng HóaĐáp án và đề thi HSG toán 6 phòng GD&ĐT Hoằng Hóa 2014-2015Đáp án đề thi HSG toán 6 phòng GD&ĐT Hoằng HóaĐáp án và đề thi HSG toán 6 phòng GD&ĐT Hoằng Hóa 2014-2015Đáp án và đề thi HSG toán 6 phòng GD&ĐT Hoằng Hóa 2014-2015
Đọc tiếp
Đề thi HSG toán 6 phòng GD&ĐT Hoằng Hóa

Đáp án và đề thi HSG toán 6 phòng GD&ĐT Hoằng Hóa 2014-2015
Đáp án đề thi HSG toán 6 phòng GD&ĐT Hoằng Hóa

Đáp án và đề thi HSG toán 6 phòng GD&ĐT Hoằng Hóa 2014-2015

Đáp án và đề thi HSG toán 6 phòng GD&ĐT Hoằng Hóa 2014-2015
Để chuẩn bị cho cuộc thi olympic khối lớp 8 cấp thành phố , phòng GD—ĐT đã đưa ra 2 phương án :_Phương án 1: bố trí 10 địa điểm thi , các địa điểm thi có số thí sinh bằng nhau ._ Phương án 2: bố trí 12 địa điểm , các địa điểm thi có số thí sinh bằng nhau.Biết rằng số thí sinh trên mỗi địa điểm của phương án 1 nhiều hơn số thí sinh trên mỗi địa điểm của phương án 2 là 7 thí sinh .Tính tổng số thí sinh dự thi olympic của khối 8.
Đọc tiếp
Để chuẩn bị cho cuộc thi olympic khối lớp 8 cấp thành phố , phòng GD—ĐT đã đưa ra 2 phương án :
_Phương án 1: bố trí 10 địa điểm thi , các địa điểm thi có số thí sinh bằng nhau .
_ Phương án 2: bố trí 12 địa điểm , các địa điểm thi có số thí sinh bằng nhau.
Biết rằng số thí sinh trên mỗi địa điểm của phương án 1 nhiều hơn số thí sinh trên mỗi địa điểm của phương án 2 là 7 thí sinh .Tính tổng số thí sinh dự thi olympic của khối 8.
Để chuẩn bị cho cuộc thi olympic khối lớp 8 cấp thành phố , phòng GD—ĐT đã đưa ra 2 phương án :_Phương án 1: bố trí 10 địa điểm thi , các địa điểm thi có số thí sinh bằng nhau ._ Phương án 2: bố trí 12 địa điểm , các địa điểm thi có số thí sinh bằng nhau.Biết rằng số thí sinh trên mỗi địa điểm của phương án 1 nhiều hơn số thí sinh trên mỗi địa điểm của phương án 2 là 7 thí sinh .Tính tổng số thí sinh dự thi olympic của khối 8
Đọc tiếp
Để chuẩn bị cho cuộc thi olympic khối lớp 8 cấp thành phố , phòng GD—ĐT đã đưa ra 2 phương án :
_Phương án 1: bố trí 10 địa điểm thi , các địa điểm thi có số thí sinh bằng nhau .
_ Phương án 2: bố trí 12 địa điểm , các địa điểm thi có số thí sinh bằng nhau.
Biết rằng số thí sinh trên mỗi địa điểm của phương án 1 nhiều hơn số thí sinh trên mỗi địa điểm của phương án 2 là 7 thí sinh .Tính tổng số thí sinh dự thi olympic của khối 8
Cùng giải đề thi vào 10 môn Toán của Sở GD&ĐT Lào Cai nhé các em.
câu 4:
hệ pt: \(\left\{{}\begin{matrix}2x-y=1\\x+y=2\end{matrix}\right.\)\(< =>\left\{{}\begin{matrix}2x-y=1\\2x+2y=4\end{matrix}\right.< =>\left\{{}\begin{matrix}-3y=-3\\2x-y=1\end{matrix}\right.\)
\(< =>\left\{{}\begin{matrix}y=1\\x=1\end{matrix}\right.\) vậy hệ phương trình có nghiệm (x,y)=(1;1)
b,
gọi thời gian làm riêng của An là x(ngày)
thời gian làm riêng của Bình là y(ngày)
=>1 ngày An làm \(\dfrac{1}{x}\)(công việc)
1 ngày Bình làm \(\dfrac{1}{y}\)(công việc)
2 người làm chung mất 2 ngày
=>pt: \(\dfrac{1}{x}+\dfrac{1}{y}=\dfrac{1}{2}\left(1\right)\)
4 ngày An làm : \(\dfrac{4}{x}\)(công việc)
vì sau 4 ngày An làm việc rồi nghỉ thì Bình làm tiếp trong 1 ngày hoàn thành công việc
=>pt: \(\dfrac{4}{x}+\dfrac{1}{y}=1\left(2\right)\)
từ(1)(2)=>\(\left\{{}\begin{matrix}\dfrac{1}{x}+\dfrac{1}{y}=\dfrac{1}{2}\\\dfrac{4}{x}+\dfrac{1}{y}=1\end{matrix}\right.\)(\(x,y\ne0\)) Đặt \(\dfrac{1}{x}=a,\dfrac{1}{y}=b\)
=>\(\left\{{}\begin{matrix}a+b=0,5\\4a+b=1\end{matrix}\right.< =>\left\{{}\begin{matrix}a=\dfrac{1}{6}\\b=\dfrac{1}{3}\end{matrix}\right.\)=>\(\left\{{}\begin{matrix}\dfrac{1}{x}=\dfrac{1}{6}\\\dfrac{1}{y}=\dfrac{1}{3}\end{matrix}\right.< =>\left\{{}\begin{matrix}x=6\left(TM\right)\\y=3\left(TM\right)\end{matrix}\right.\)
vậy AN làm công việc riêng trong 6 ngày
Bình làm riêng trong 3 ngày
Đúng 2
Bình luận (0)
Câu 1.
a) `A=\sqrt49-3=\sqrt(7^2)-3=7-3=4`
b) `B=\sqrt((10-\sqrt5)^2)+\sqrt5`
`=10-\sqrt5+\sqrt5`
`=10`
Câu 2.
a) `P=(\sqrtx/(\sqrtx+2)+2/(\sqrtx-2)) : (x+4)/(\sqrtx+2)`
`= (\sqrtx(\sqrtx-2)+2(\sqrtx+2))/((\sqrtx+2)(\sqrtx-2)) . (\sqrtx-2)/(x+4)`
`=(x+4)/((\sqrtx+2)(\sqrtx-2)) . (\sqrtx+2)/(x+4)`
`=1/(\sqrtx-2)`
b) `P=1/6 <=> 1/(\sqrtx-2) = 1/6`
`<=> \sqrtx-2=6`
`<=> \sqrtx=8`
`<=> x=64`
Câu 3.
a) Đồ thị cắt trục hoành tại điểm có hoành độ là 3 `=> (3;0) \in y=2x+b`
`<=> 0=2.3+b <=> b=-6`
`=>y=2x-6`
b) Phương trình hoành độ giao điểm:
`x^2=(m-1)x+m+4`
`<=>x^2-(m-1)x-m-4=0` (1)
2 giao điểm của 2 đồ thị nằm về 2 phía của trục tung `<=>` PT (1) có 2 nghiệm trái dấu.
`<=> 1.(-m-4) <0`
`<=> m> -4`
Đúng 4
Bình luận (0)
Câu 4
a)
\(\left\{{}\begin{matrix}2x-y=1\\x+y=2\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}3x=3\\x+y=3\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}x=1\\1+y=3\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}x=1\\y=2\end{matrix}\right.\)
b)
Gọi thời gian 2 bạn An và Bình làm riêng lần lượt là `x,y` (ngày) `(x;y>0)`
- Trong 1 ngày mỗi bạn làm được:
An : `1/x` (công việc)
Bình: `1/y` (công việc)
Mà sau 2 ngày làm chung thì hoàn thành
`=> 2/x+2/y=1` (1)
- An làm trong 4 ngày rồi nghỉ, Bình làm tiếp trong 1 ngày thì hoàn thành.
`=> 4/x+1/y=1` (2)
Từ (1) và (2) ta có hệ: \(\left\{{}\begin{matrix}\dfrac{2}{x}+\dfrac{2}{y}=1\\\dfrac{4}{x}+\dfrac{1}{y}=1\end{matrix}\right.\)
Giải hệ ta được: \(\left\{{}\begin{matrix}x=6\\y=3\end{matrix}\right.\)
Vậy nếu làm riêng thì An mất 6 ngày, Bình mất 3 ngày để hoàn thành.
Câu 5.
a) `x^2+5x-6=0`
Ta có: `\Delta = 5^2-4.1.(-6)=49>0`
`=>` PT có 2 nghiệm phân biệt:
`x_1=(-5+\sqrt49)/2=1`
`x_2=(-5-\sqrt49)/2=-6`
Vậy `x_1=1;x_2=-6`.
b) PT có 2 nghiệm `<=> \Delta >=0`
`<=> m^2-4(m-2)>=0`
`<=> m^2-4m+8>=0`
`<=> (m^2-4m+4)+4>=0`
`<=>(m-2)^2+4>=0 forall m`
`=>` PT có 2 nghiệm với mọi `m`.
Theo hệ thức Viet: `x_1+x_2=m`
`x_1x_2=m-2`
Ta có: `x_1-x_2=2\sqrt5`
`<=>\sqrt((x_1+x_2)^2-4x_1x_2) =2\sqrt5`
`<=> (x_1+x_2)^2-4x_1x_2=20 (x_1>x_2)`
`<=> m^2-4(m-2)=20`
`<=>m^2-4m-12=0`
`<=>` \(\left[{}\begin{matrix}m=6\\m=-2\end{matrix}\right.\)
Vậy `m=6; m=-2`.
Đúng 3
Bình luận (0)
Xem thêm câu trả lời
Cho tứ giác ABCD. Gọi I ; K lần lượt là trung điểm của AB; CD. Xác định vị trí điểm G sao cho:
G
A
→
+
G
B
→
+
G
C
→
+
G
D
→
0
→
A. G là trung điểm của BI B. G là...
Đọc tiếp
Cho tứ giác ABCD. Gọi I ; K lần lượt là trung điểm của AB; CD. Xác định vị trí điểm G sao cho: G A → + G B → + G C → + G D → = 0 →
A. G là trung điểm của BI
B. G là trung điểm của KD
C. G là trung điểm của BD
D. G là trung điểm của IK
Cho tứ giác ABCD. Gọi I ; K lần lượt là trung điểm của AB; CD. Xác định vị trí điểm G sao cho
G
A
→
+
G
B
→
+
G
C
→
+
G
D
→
0...
Đọc tiếp
Cho tứ giác ABCD. Gọi I ; K lần lượt là trung điểm của AB; CD. Xác định vị trí điểm G sao cho G A → + G B → + G C → + G D → = 0 →
A. G là trung điểm của BI
B. G là trung điểm của KD
C. G là trung điểm của BD
D. G là trung điểm của IK
(Sở GD – ĐT Ninh Bình – lần 2 2019): Phân tử ADN của một loài động vật gồm 30 chu kỳ xoắn và có X50. số nuclêôtit loại T của phân tử ADN này là: A. 300 B. 250 C. 600 D. 50
Đọc tiếp
(Sở GD – ĐT Ninh Bình – lần 2 2019): Phân tử ADN của một loài động vật gồm 30 chu kỳ xoắn và có X=50. số nuclêôtit loại T của phân tử ADN này là:
A. 300
B. 250
C. 600
D. 50
Đáp án B
N = 30×20=600 =2X + 2T ; X=50 → T= 250
Đúng 0
Bình luận (0)
Các bạn cùng thử sức với đề thi vào 10 THPT chuyên của Sở GD&ĐT Hà Nam nhé.
Câu 1
1) \(A=\sqrt{20}-\sqrt{45}+\sqrt{6+2\sqrt{5}}\)
\(=2\sqrt{5}-3\sqrt{5}+\sqrt{\left(\sqrt{5}\right)^2+2\sqrt{5}+1}\)
\(=-\sqrt{5}+\sqrt{\left(\sqrt{5}+1\right)^2}\)
\(=-\sqrt{5}+\sqrt{5}+1\)
\(=1\)
2) ĐKXĐ: \(x>0;x\ne1\)
\(B=\left(\dfrac{1}{x-\sqrt{x}}+\dfrac{1}{\sqrt{x}-1}\right):\dfrac{\sqrt{x}+1}{\left(\sqrt{x}-1\right)^2}\)
\(=\left(\dfrac{1}{\sqrt{x}\left(\sqrt{x}-1\right)}+\dfrac{1}{\sqrt{x}-1}\right).\dfrac{\left(\sqrt{x}-1\right)^2}{\sqrt{x}+1}\)
\(=\dfrac{1+\sqrt{x}}{\sqrt{x}\left(\sqrt{x}-1\right)}.\dfrac{\left(\sqrt{x}-1\right)^2}{\sqrt{x}+1}\)
\(=\dfrac{\sqrt{x}-1}{\sqrt{x}}\)
\(\Rightarrow B=\dfrac{\sqrt{x}-1}{\sqrt{x}}=\dfrac{1}{2}\)
\(\Leftrightarrow2\left(\sqrt{x}-1\right)=\sqrt{x}\)
\(\Leftrightarrow2\sqrt{x}-2=\sqrt{x}\)
\(\Leftrightarrow2\sqrt{x}-\sqrt{x}=2\)
\(\Leftrightarrow\sqrt{x}=2\)
\(\Rightarrow x=4\left(tmđk\right)\)
Đúng 5
Bình luận (0)
Câu 5 :
Ta có : \(6a+3b+2c=abc\) \(\Rightarrow\dfrac{6}{bc}+\dfrac{3}{ac}+\dfrac{2}{ab}=1\)
Đặt : \(\left\{{}\begin{matrix}\dfrac{1}{a}=x\\\dfrac{2}{b}=y\\\dfrac{3}{c}=z\end{matrix}\right.\) với \(x,y,z>0\) \(\Rightarrow xy+yz+zx=1\)
Ta biến đổi : \(\dfrac{1}{\sqrt{a^2+1}}=\sqrt{\dfrac{\dfrac{1}{a^2}}{1+\dfrac{1}{a^2}}}=\sqrt{\dfrac{x^2}{1+x^2}}=\sqrt{\dfrac{x^2}{xy+xz+yz+x^2}}=\sqrt{\dfrac{x^2}{\left(x+y\right)\left(x+z\right)}}\)
Chứng minh tương tự ta có :
\(\dfrac{1}{\sqrt{b^2+4}}=\sqrt{\dfrac{y^2}{\left(y+z\right)\left(y+x\right)}}\) ; \(\dfrac{1}{\sqrt{c^2+9}}=\sqrt{\dfrac{z^2}{\left(z+x\right)\left(z+y\right)}}\)
Do đó : \(Q=\sqrt{\dfrac{x^2}{\left(x+z\right)\left(x+y\right)}}+\sqrt{\dfrac{y^2}{\left(y+z\right)\left(y+x\right)}}+\sqrt{\dfrac{z^2}{\left(z+x\right)\left(z+y\right)}}\)
Áp dụng BĐT Cô - si ta được :
\(Q=\sqrt{\dfrac{x^2}{\left(x+z\right)\left(x+y\right)}}+\sqrt{\dfrac{y^2}{\left(y+z\right)\left(y+x\right)}}+\sqrt{\dfrac{z^2}{\left(z+x\right)\left(z+y\right)}}\)
\(\le\dfrac{1}{2}\left(\dfrac{x}{x+z}+\dfrac{x}{x+y}+\dfrac{y}{y+z}+\dfrac{y}{y+x}+\dfrac{z}{z+x}+\dfrac{z}{z+y}\right)\)
\(=\dfrac{1}{2}\left(\dfrac{x+z}{x+z}+\dfrac{x+y}{x+y}+\dfrac{z+y}{z+y}\right)=\dfrac{1}{2}\cdot3=\dfrac{3}{2}\)
Dấu "=" xảy ra khi \(\left\{{}\begin{matrix}a=\sqrt{3}\\b=2\sqrt{3}\\c=3\sqrt{3}\end{matrix}\right.\)
Vậy Max \(P=\dfrac{3}{2}\) khi \(\left\{{}\begin{matrix}a=\sqrt{3}\\b=2\sqrt{3}\\c=3\sqrt{3}\end{matrix}\right.\)
Đúng 3
Bình luận (0)
Câu 2
1) Phương trình \(x^2-6x+5=0\) có:
\(a+b+c=1-6+5=0\)
\(\Rightarrow\) Phương trình có hai nghiệm phân biệt \(x_1=1\) và \(x_2=\dfrac{c}{a}=5\)
2) \(\left\{{}\begin{matrix}2\left(x+2\right)=3\left(y-1\right)\\3x+y=6\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}2x+4=3y-3\\3x+y=6\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}2x-3y=-7\\3x+y=6\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}2x-3y=-7\\9x+3y=18\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}11x=11\\3x+y=6\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x=1\\3+y=6\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x=1\\y=3\end{matrix}\right.\)
Đúng 6
Bình luận (0)
Xem thêm câu trả lời
(Sở GD và ĐT Hà Nội – Hà Nội 2017). Số dân nước ta ít hơn số dân những quốc gia nào sau đây?
A. Malaixia, Thái Lan
B. Inđônêxia, Philipin
C. Inđônêxia, Lào
D. Philippin, Mianma
Hướng dẫn: SGK/67, địa lí 12 cơ bản.
Chọn: C
Đúng 0
Bình luận (0)