Các câu hỏi tương tự
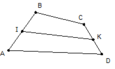
Cho hình chóp s.abcd , có đáy ABCD là hbh. Gọi H, K lần lượt là trung điểm SA, SC. Gọi G là trọng tâm tam giác ABC.
a) GHK và ABCD
b) Tìm giao điểm M của SD và GHK
c) Gọi E là trung điểm của HK. C/m G, E, M thẳng hàng
Cho hình chóp s.abcd đáy là hbh. Gọi H K lần lượt là trung điểm SA SC. G là trọng tâm tam giác ABC a)GHK và ABCD b) Tìm giao điểm M của SD và GHK c) Gọi E là trung điểm của HK.C/m G E M thẳng hàng
Cho hình chóp S.ABCD, ABCD là hình thang, đáy lớn AD=2BC. Gọi M, N lần lượt là trung điểm của AD, CD. a/. Chứng minh: MN//(SAC). b/. Gọi K SB sao cho KB 2KS . Xác định giao điểm của đường thẳng SA và (MNK). c/. Gọi G là trọng tâm tam giác CDM. Chứng minh KG//SD.
Cho tứ diện ABCD. Gọi M,N,P lần lượt là trung điểm của các cạnh BC, BD,CD.
a. Xác định giao tuyến của hai mặt phẳng (AMN) và (ACD).
b. Chứng minh rằng đường thẳng BC song song với mặt phẳng (ANP)
c. Gọi G, H lần lượt là trọng tâm của tam giác ABC và ACD. Chứng minh GH // BD.
Cho hình hộp ABCD.A’B’C’D’. Gọi M, N lần lượt là trung điểm của CD và DD’; G và G’ lần lượt là trọng tâm của hai tứ diện A’D’NM và BCC’D’. Đặt
A
B
→
a
→
;
A
A
→
b
→
;
...
Đọc tiếp
Cho hình hộp ABCD.A’B’C’D’. Gọi M, N lần lượt là trung điểm của CD và DD’; G và G’ lần lượt là trọng tâm của hai tứ diện A’D’NM và BCC’D’. Đặt A B → = a → ; A A ' → = b → ; A D → = c → .
Vecto M N → bằng:
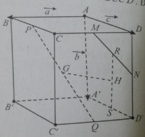
A. 1 2 c → - a →
B. 1 2 c → - b →
C. 1 2 b → - a →
D. 1 2 a → - b →
Cho tứ diện ABCD. Gọi M, N lần lượt là trung điểm của các cạnh AB, CD và G là trung điểm của đoạn MN.
a) Tìm giao điểm A’ của đường thẳng AG và mp(BCD).
b) Qua M kẻ đường thẳng Mx song song với AA’ và Mx cắt (BCD) tại M’.
c) Chứng minh GA = 3GA’
Cho tứ diện ABCD với G là trọng tâm và các điểm M, N, P, Q, I, J lần lượt là trung điểm của các cạnh AB, BC, CD, AD, AC, BD.
A
B
→
+
A
C
→
+
A
D
→
bằng: A.
4
A
G...
Đọc tiếp
Cho tứ diện ABCD với G là trọng tâm và các điểm M, N, P, Q, I, J lần lượt là trung điểm của các cạnh AB, BC, CD, AD, AC, BD.
A B → + A C → + A D → bằng:
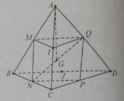
A. 4 A G →
B. 2 A G →
C. A G →
D. 1 / 2 A G →
Cho hình hộp ABCD.A’B’C’D’. Gọi M, N lần lượt là trung điểm của CD và DD’; G và G’ lần lượt là trọng tâm của hai tứ diện A’D’NM và BCC’D’. Đặt
A
B
→
a
→
;
A
A
→
b
→
;
...
Đọc tiếp
Cho hình hộp ABCD.A’B’C’D’. Gọi M, N lần lượt là trung điểm của CD và DD’; G và G’ lần lượt là trọng tâm của hai tứ diện A’D’NM và BCC’D’. Đặt A B → = a → ; A A ' → = b → ; A D → = c → .
Đường thẳng GG’ song song với mặt phẳng (AA’B’B) vì:
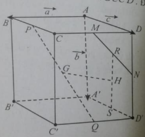
A. Vecto G G ' → cùng phương với vecto C D →
B. Vecto G G ' → cùng phương với vecto M N →
C. Vecto G G ' → đồng phẳng với hai vecto a → v à b →
D. Vecto G G ' → đồng phẳng với hai vecto b → v à c → .
Cho tứ diện ABCD có E và F lần lượt là trung điểm của AB và CD; G là trọng tâm tam giác BCD. Giao điểm của đường thẳng EG và mp (ACD) là
A. điểm F
B. giao điểm của EG và AF
C. Giao điểm của EG và AC
D. giao điểm của EG và CD