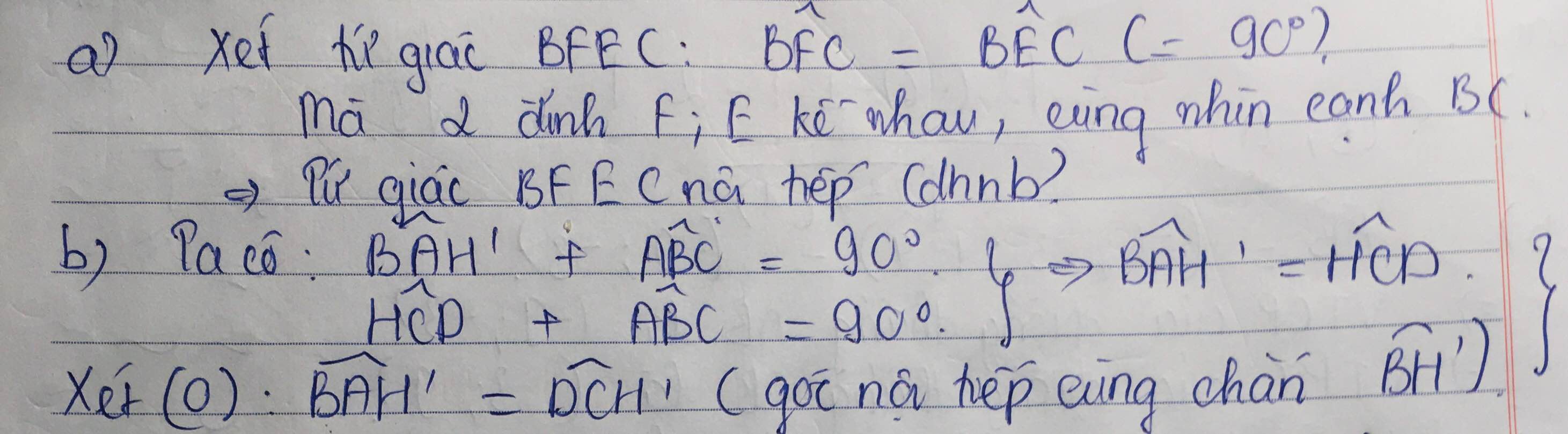giúp mình câu b với c với
giúp mình câu b với c với

Những câu hỏi liên quan
giúp mình bài 6 với ạ trừ câu a còn các câu b,c,d, giúp mình với ạ
Đọc tiếp
giúp mình bài 6 với ạ trừ câu a còn các câu b,c,d, giúp mình với ạ
\(b,N=\left(2x-1\right)^2-4\ge-4\\ N_{min}=-4\Leftrightarrow x=\dfrac{1}{2}\\ c,P=\left(2x-5\right)^2+6\left(2x-5\right)+9-4\\ P=\left(2x-5+3\right)^2-4=\left(2x-2\right)^2-4\ge-4\\ P_{min}=-4\Leftrightarrow x=1\\ d,Q=\left(x^2-2x+1\right)+\left(y^2+4y+4\right)+1\\ Q=\left(x-1\right)^2+\left(y+2\right)^2+1\ge1\\ Q_{min}=1\Leftrightarrow\left\{{}\begin{matrix}x=1\\y=-2\end{matrix}\right.\)
Đúng 4
Bình luận (0)
6a.
$M=x^2-x+1=(x^2-x+\frac{1}{4})+\frac{3}{4}$
$=(x-\frac{1}{2})^2+\frac{3}{4}\geq \frac{3}{4}$
Vậy $M_{\min}=\frac{3}{4}$ khi $x-\frac{1}{2}=0\Leftrightarrow x=\frac{1}{2}$
Đúng 1
Bình luận (0)
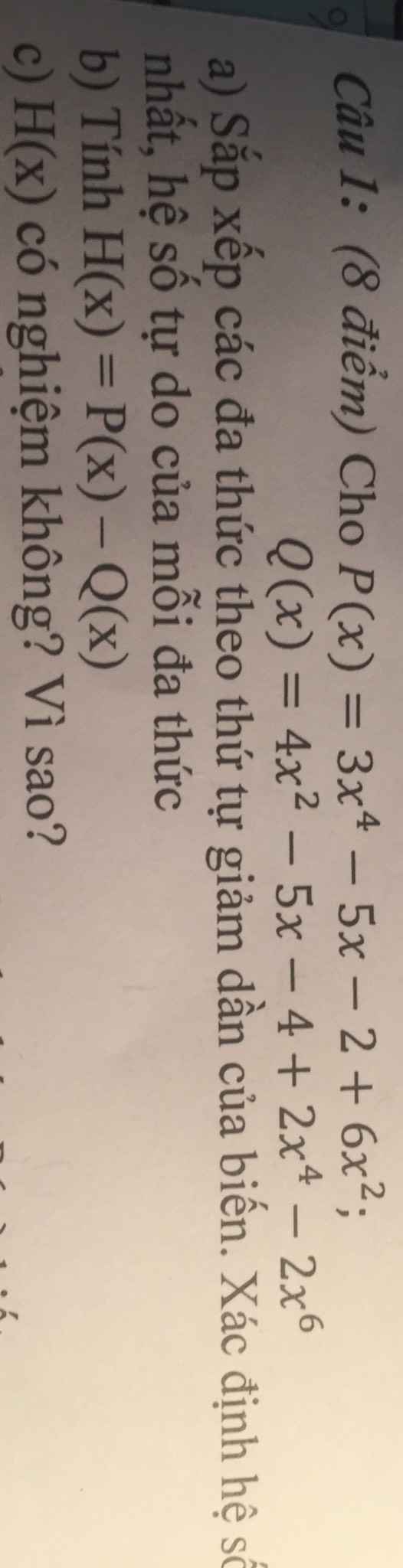
Làm giúp mình câu b với câu c với
a: P(x)=3x^4+6x^2-5x-2
Q(x)=-2x^6+2x^4+4x^2-5x-4
b: H(x)=P(x)-Q(x)
=3x^4+6x^2-5x-2+2x^6-2x^4-4x^2+5x+4
=2x^6+x^4+2x^2+2
c: H(x)=x^2(2x^4+x^2+2)+2>=2>0 với mọi x
=>H(x) ko có nghiệm
Đúng 0
Bình luận (0)
Giúp mình câu b và câu c với 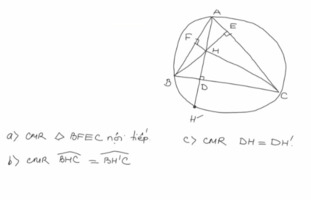
![]() giúp mình câu b,c câu 38 với mọi người
giúp mình câu b,c câu 38 với mọi người![]()

Giúp mình phần câu b,c với ạ mình cần gấp 



Giúp mình câu b và c với

Giúp mình câu b, c với ạ
Mn giúp mình câu b,c với 
giúp mình câu b và c với