Chứng minh rằng
\(\dfrac{1}{2020.2021}=\dfrac{1}{2020-2021}\)
Những câu hỏi liên quan
Cho B = 1.2.3.....2020.(\(1+\dfrac{1}2+\frac{1}{3}+.......+\frac{1}{2020}\) Chứng minh rằng B chia hết cho 2021.
chứng minh bất đẳng thức sau: \(\dfrac{2020}{\sqrt{2021}}+\dfrac{\sqrt{2021}}{2020}>\sqrt{2020}+\sqrt{2021}\)
13 tháng 12 2022 lúc 20:44
Cho \(\dfrac{x}{2020}+\dfrac{y}{2021}+\dfrac{z}{2022}=1\) và \(\dfrac{2020}{x}+\dfrac{2021}{y}+\dfrac{2022}{z}=0\) \(\left(x,y,z\ne0\right)\)
Chứng minh rằng \(\dfrac{x^2}{2020^2}+\dfrac{y^2}{2021^2}+\dfrac{z^2}{2022^2}=1\)
cho A=\(\dfrac{1}{2^2}\)+\(\dfrac{1}{2^3}\)+\(\dfrac{1}{2^4}\)+.....+\(\dfrac{1}{2^{2020}}\)+\(\dfrac{1}{2^{2021}}\). Chứng tỏ rằng A<\(\dfrac{1}{2}\)
Giúp vs ạ cần gấp
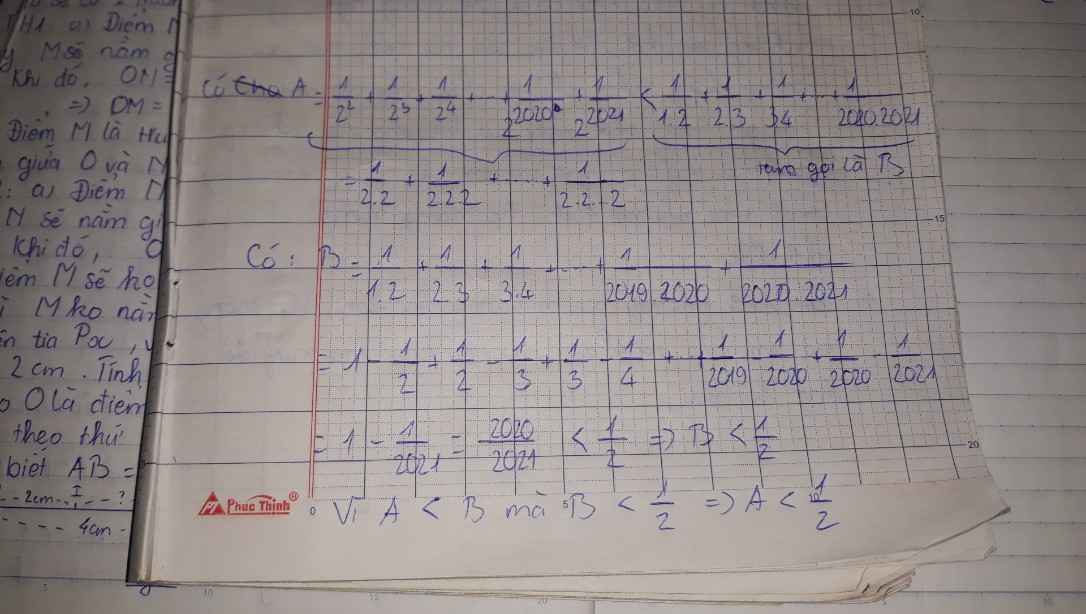
làm vào bài đừng có dùng ngoặc kép như tui nha,tui làm minh họa cho bạn hiểu
Đúng 0
Bình luận (0)
Chứng minh rằng :
\(2021-\left(1+\dfrac{1}{2}+\dfrac{1}{3}+...+\dfrac{1}{2021}\right)=\dfrac{1}{2}+\dfrac{2}{3}+\dfrac{3}{4}+...+\dfrac{2020}{2021}\)
\(2021-\left(1+\dfrac{1}{2}+\dfrac{1}{3}+...+\dfrac{1}{2021}\right)\)
\(=\left(1-1\right)+\left(1-\dfrac{1}{2}\right)+\left(1-\dfrac{1}{3}\right)+...+\left(1-\dfrac{1}{2021}\right)\)
\(=\dfrac{1}{2}+\dfrac{2}{3}+\dfrac{3}{4}+...+\dfrac{2020}{2021}\)
Đúng 1
Bình luận (0)
Giải:
\(2021-\left(1+\dfrac{1}{2}+\dfrac{1}{3}+...+\dfrac{1}{2021}\right)=\dfrac{1}{2}+\dfrac{2}{3}+\dfrac{3}{4}+...+\dfrac{2020}{2021}\)
Ta có:
\(2021-\left(1+\dfrac{1}{2}+\dfrac{1}{3}+...+\dfrac{1}{2021}\right)\)
\(=\left(1-1\right)+\left(1-\dfrac{1}{2}\right)+\left(1-\dfrac{1}{3}\right)+...+\left(1-\dfrac{1}{2021}\right)\)
\(=0+\dfrac{1}{2}+\dfrac{2}{3}+...+\dfrac{2020}{2021}\)
\(=\dfrac{1}{2}+\dfrac{2}{3}+...+\dfrac{2020}{2021}\)
Mà \(\dfrac{1}{2}+\dfrac{2}{3}+...+\dfrac{2020}{2021}=\dfrac{1}{2}+\dfrac{2}{3}+\dfrac{3}{4}+...+\dfrac{2020}{2021}\)
\(\Rightarrow2021-\left(1+\dfrac{1}{2}+\dfrac{1}{3}+...+\dfrac{1}{2021}\right)=\dfrac{1}{2}+\dfrac{2}{3}+\dfrac{3}{4}+...+\dfrac{2020}{2021}\left(đpcm\right)\)
Đúng 0
Bình luận (0)
cho 3 số a,b,c thoả mãn \(\dfrac{a}{2020}=\dfrac{b}{2021}=\dfrac{c}{2022}\)
Chứng minh rằng (a-c)3+8(a-b)2.(c-b)=0
Bài này xuất hiện trong câu cuối đề GKI năm ngoái của mình :v
-Áp dụng tính chất của dãy tỉ số bằng nhau ta có:
\(\left\{{}\begin{matrix}\dfrac{a}{2020}=\dfrac{c}{2022}=\dfrac{a-c}{2020-2022}=\dfrac{a-c}{-2}\\\dfrac{a}{2020}=\dfrac{b}{2021}=\dfrac{a-b}{2020-2021}=\dfrac{a-b}{-1}\\\dfrac{c}{2022}=\dfrac{b}{2021}=\dfrac{c-b}{2022-2021}=c-b\end{matrix}\right.\)
\(\Rightarrow c-b=-\left(a-b\right)=\dfrac{a-c}{-2}\)
\(\Rightarrow\left\{{}\begin{matrix}a-c=-2\left(c-b\right)\\a-b=-\left(c-b\right)\end{matrix}\right.\)
\(\left(a-c\right)^3+8\left(a-b\right)^2.\left(c-b\right)=\left[-2\left(c-b\right)\right]^3+8\left[-\left(c-b\right)\right]^2.\left(c-b\right)=-8\left(c-b\right)^3+8\left(c-b\right)^3=0\left(đpcm\right)\)
Đúng 0
Bình luận (0)
a) Tìm số tự nhiên n biết:
\(\dfrac{4}{3\cdot5}+\dfrac{8}{5\cdot9}+\dfrac{12}{9\cdot15}+....+\dfrac{32}{n\cdot\left(n+16\right)}=\dfrac{16}{25}\)
b) Chứng tỏ rằng:
\(\dfrac{2018}{2019}+\dfrac{2019}{2020}+\dfrac{2020}{2021}+\dfrac{2021}{2018}>4\)
a) \(2\left(\dfrac{2}{3.5}+\dfrac{4}{5.9}+...+\dfrac{16}{n\left(n+16\right)}\right)=\dfrac{16}{25}\)
\(\dfrac{1}{3}-\dfrac{1}{5}+\dfrac{1}{5}-\dfrac{1}{9}+...+\dfrac{1}{n}-\dfrac{1}{n+16}=\dfrac{8}{25}\)
\(\dfrac{1}{3}-\dfrac{1}{n+16}=\dfrac{8}{25}\)
\(\dfrac{n+13}{3\left(n+16\right)}=\dfrac{8}{25}\)
\(24n+384=25n+325\)
\(25n-24n=384-325\)
\(n=59\)
Đúng 0
Bình luận (0)
b) Sai đề nha
\(\left\{{}\begin{matrix}\dfrac{2018}{2019}< 1\\\dfrac{2019}{2020}< 1\\\dfrac{2020}{2021}< 1\\\dfrac{2021}{2022}< 1\end{matrix}\right.\)
\(\Rightarrow\dfrac{2018}{2019}+\dfrac{2019}{2020}+\dfrac{2020}{2021}+\dfrac{2021}{2022}< 4\)
Đúng 0
Bình luận (0)
chị ơi hình như chị nhầm rồi P/s cuối phải là 1/n.(n+6)thì phải
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
B=\(\dfrac{\dfrac{1}{2020}+\dfrac{1}{2021}-\dfrac{1}{2022}}{\dfrac{3}{2020}+\dfrac{3}{2021}-\dfrac{3}{2022}}-1\)
\(B=\dfrac{\dfrac{1}{2020}+\dfrac{1}{2021}-\dfrac{1}{2022}}{\dfrac{3}{2020}+\dfrac{3}{2021}-\dfrac{3}{2022}}-1=\dfrac{\dfrac{1}{2020}+\dfrac{1}{2021}-\dfrac{1}{2022}}{3\left(\dfrac{1}{2020}+\dfrac{1}{2021}-\dfrac{1}{2022}\right)}-1=\dfrac{1}{3}-1=-\dfrac{2}{3}\)
Đúng 2
Bình luận (0)
\(B=\dfrac{\dfrac{1}{2021}+\dfrac{1}{2021}-\dfrac{1}{2022}}{\dfrac{3}{2020}+\dfrac{3}{2021}-\dfrac{3}{2022}}-1=\dfrac{\dfrac{1}{2021}+\dfrac{1}{2021}-\dfrac{1}{2022}}{3\left(\dfrac{1}{2020}+\dfrac{1}{2021}-\dfrac{1}{2022}\right)}-1=\dfrac{1}{3}-1=\dfrac{1}{3}-\dfrac{3}{3}=-\dfrac{2}{3}\)
Đúng 1
Bình luận (0)
Xem thêm câu trả lời
a)Cho A dfrac{2015}{2016}+dfrac{2016}{2017}+dfrac{2017}{2018}+dfrac{2018}{2019}+dfrac{2019}{2020}+dfrac{2021}{2015}
Chứng minh A6
b)Cho Cdfrac{1}{3}+dfrac{1}{3^2}+dfrac{1}{3^3}+....+dfrac{1}{3^{2010}}
Chứng minh rằng C1
Cho Ddfrac{1}{1^2.2^3}+dfrac{5}{2^2.3^3}+dfrac{7}{3^2.4^2}+.....+dfrac{4019}{2009^2.2010^2}
Chứng minh rằng D1
mấy bạn giúp mình nha. Mình cần gấp lắm TT^TT
Đọc tiếp
a)Cho A= \(\dfrac{2015}{2016}+\dfrac{2016}{2017}+\dfrac{2017}{2018}+\dfrac{2018}{2019}+\dfrac{2019}{2020}+\dfrac{2021}{2015}\)
Chứng minh A>6
b)Cho C=\(\dfrac{1}{3}+\dfrac{1}{3^2}+\dfrac{1}{3^3}+....+\dfrac{1}{3^{2010}}\)
Chứng minh rằng C<1
Cho D=\(\dfrac{1}{1^2.2^3}+\dfrac{5}{2^2.3^3}+\dfrac{7}{3^2.4^2}+.....+\dfrac{4019}{2009^2.2010^2}\)
Chứng minh rằng D<1
mấy bạn giúp mình nha. Mình cần gấp lắm TT^TT
mấy bạn ơi câu b) là chứng minh C<\(\dfrac{1}{2}\)nha
Đúng 0
Bình luận (0)