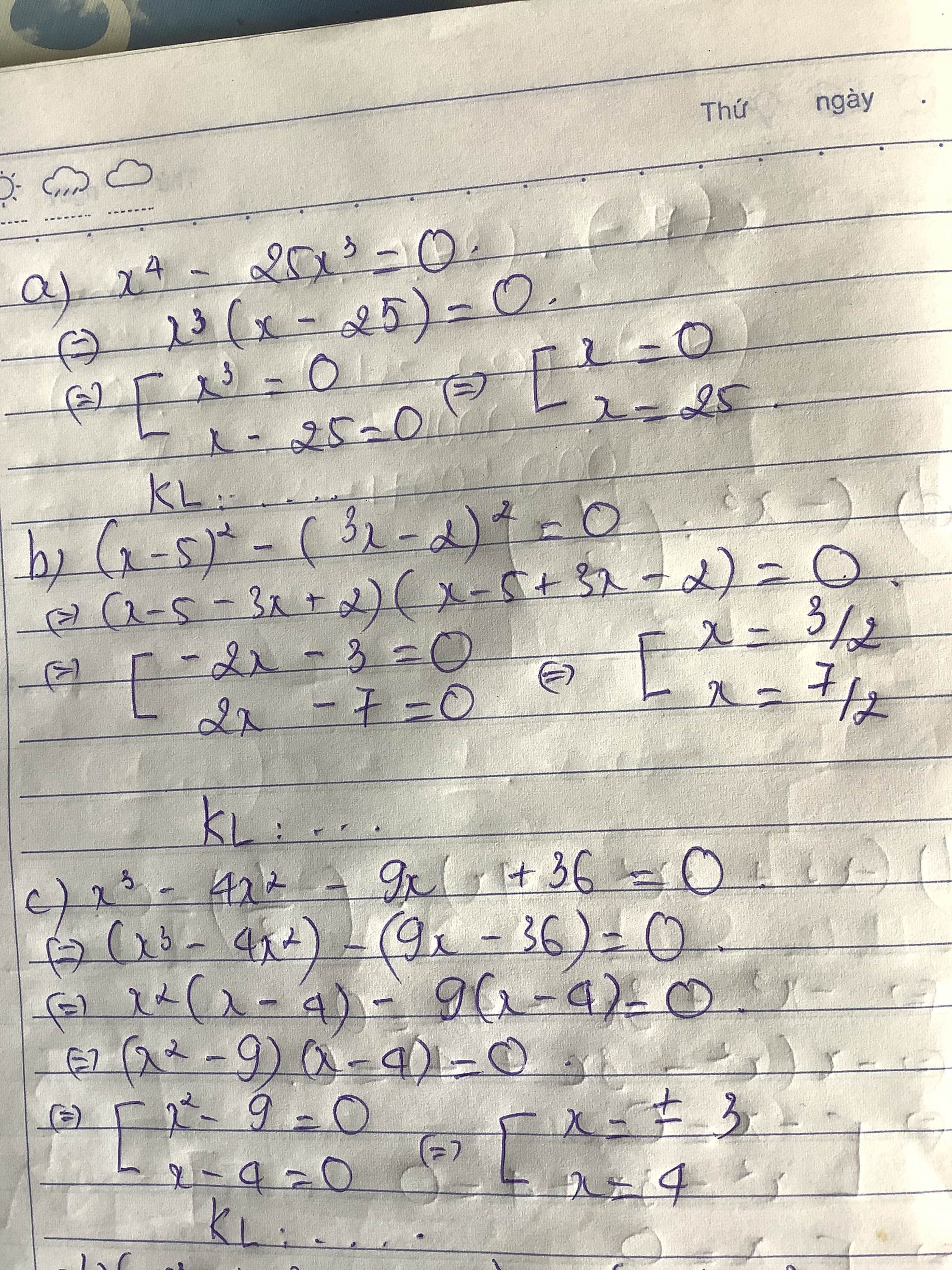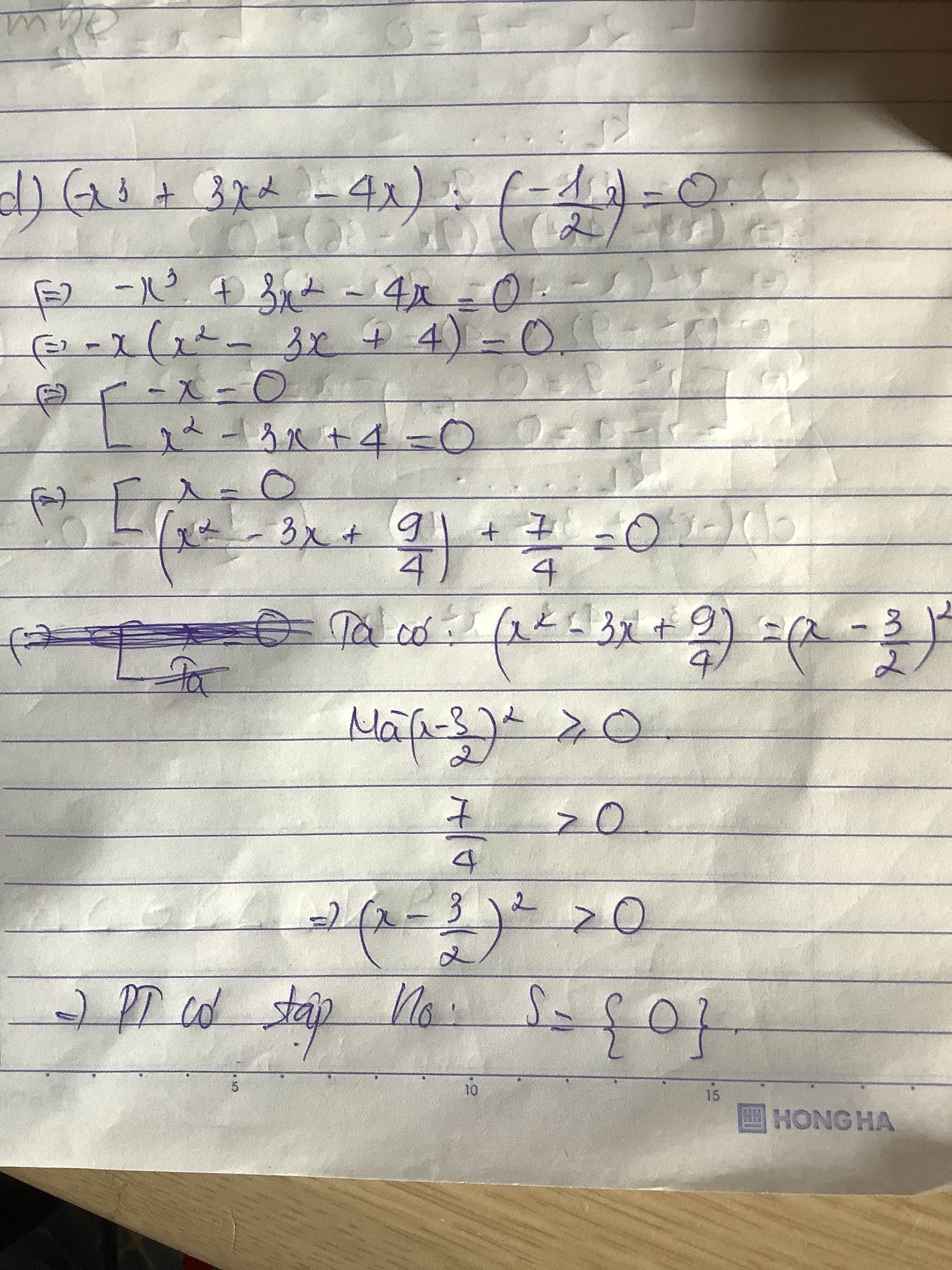x3- 4x =0 tìm x

Những câu hỏi liên quan
Tìm x biết: a. x3 – 25x 0 b. 3x(x- 2) – x + 2 0 c. x2 – 4x - 5 0 d.x3 – x2 + 3x – 3 0 e. x3 + 27 + ( x + 3)( x – 9) 0
Đọc tiếp
Tìm x biết:
a. x3 – 25x = 0 b. 3x(x- 2) – x + 2 = 0
c. x2 – 4x - 5 = 0 d.x3 – x2 + 3x – 3 = 0
e. x3 + 27 + ( x + 3)( x – 9) = 0
a: \(\Leftrightarrow x\left(x-5\right)\left(x+5\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=0\\x=5\\x=-5\end{matrix}\right.\)
Đúng 0
Bình luận (0)
Bài 2: Tìm x, biết:
a) 4x(x + 1) = 8( x + 1) c) x2 – 6x + 8 = 0
b) x3 + x2 + x + 1 = 0 d) x3 – 7x – 6 = 0
\(a,\Leftrightarrow\left(4x-8\right)\left(x+1\right)=0\\ \Leftrightarrow4\left(x-2\right)\left(x+1\right)=0\Leftrightarrow\left[{}\begin{matrix}x=2\\x=-1\end{matrix}\right.\\ b,\Leftrightarrow\left(x+1\right)\left(x^2+1\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}x=-1\\x^2=-1\left(vô.lí\right)\end{matrix}\right.\Leftrightarrow x=-1\\ c,\Leftrightarrow x^2-2x-4x+8=0\\ \Leftrightarrow\left(x-2\right)\left(x-4\right)=0\Leftrightarrow\left[{}\begin{matrix}x=2\\x=4\end{matrix}\right.\\ d,\Leftrightarrow x^3-3x^2+3x-9x+2x-6=0\\ \Leftrightarrow\left(x-3\right)\left(x^2+3x+2\right)=0\\ \Leftrightarrow\left(x-3\right)\left(x^2+x+2x+2\right)=0\\ \Leftrightarrow\left(x-3\right)\left(x+1\right)\left(x+2\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}x=3\\x=-1\\x=-2\end{matrix}\right.\)
Đúng 1
Bình luận (0)
a) \(\Rightarrow4\left(x+1\right)\left(x-2\right)=0\)
\(\Rightarrow\left[{}\begin{matrix}x=-1\\x=2\end{matrix}\right.\)
b) \(\Rightarrow x^2\left(x+1\right)+\left(x+1\right)=0\)
\(\Rightarrow\left(x+1\right)\left(x^2+1\right)=0\)
\(\Rightarrow x=-1\left(do.x^2+1\ge1>0\right)\)
c) \(\Rightarrow x\left(x-4\right)-2\left(x-4\right)=0\)
\(\Rightarrow\left(x-4\right)\left(x-2\right)=0\)
\(\Rightarrow\left[{}\begin{matrix}x=4\\x=2\end{matrix}\right.\)
d) \(\Rightarrow x^2\left(x-3\right)+3x\left(x-3\right)+2\left(x-3\right)\)
\(\Rightarrow\left(x-3\right)\left(x^2+3x+2\right)=0\)
\(\Rightarrow\left(x-3\right)\left(x+1\right)\left(x+2\right)=0\)
\(\Rightarrow\left[{}\begin{matrix}x=3\\x=-2\\x=-1\end{matrix}\right.\)
Đúng 1
Bình luận (0)
Tìm x
a) 4x(x+1)-x-1 = 0
b) x3-4x2+4x =0
c) x2-3x + 2 =0
tham khảo: https://hoc24.vn/cau-hoi/.2256230161739
Đúng 0
Bình luận (0)
a) ⇔ \(4x^2+4x-x-1=0\)
⇔ \(4x^2+3x-1=0\)
⇔ \(4x(x+1)-(x+1)=0\)
⇔ \((x+1)(4x-1)=0\)
⇒ \(\left[{}\begin{matrix}x=-1\\x=\dfrac{1}{4}\end{matrix}\right.\)
Vậy...
b) \(x^3-4x^2+4x=0\)
⇔ \(x^2(x-2)-2x(x-2)=0\)
⇔ \((x-2)(x^2-2x)=0\)
⇒ \(\left[{}\begin{matrix}x=2\\x=0\end{matrix}\right.\)
Vậy...
c) \(x^2-3x+2=0\)
⇔ \(x(x-2)-(x-2)=0\)
⇔ \((x-1)(x-2)=0\)
⇒ \(\left[{}\begin{matrix}x=1\\x=2\end{matrix}\right.\)
Vậy...
Đúng 1
Bình luận (0)
Tìm x, biết rằng: x 3 - 4 x = 0
Phân tích ra: x ( x – 2 ) ( x + 2 ) = 0
⇒ x = 0 , x = ± 2
Đúng 0
Bình luận (0)
Tìm x, biết:a) 2-x 2
(
x
-
2
)
3
; b) 8
x
3
- 72x 0;c)
(
x
-
1
,
5
)
6
+
...
Đọc tiếp
Tìm x, biết:
a) 2-x = 2 ( x - 2 ) 3 ; b) 8 x 3 - 72x = 0;
c) ( x - 1 , 5 ) 6 + 2 ( 1 , 5 - x ) 2 = 0; d) 2 x 3 +3 x 2 +3 + 2x = 0;
e) x 3 - 4x- 14x(x - 2) = 0; g) x 2 (x + 1)- x(x + 1) + x(x - 1) = 0.
Phân tích các đa thức sau thành nhân tử
a, 3xy2 – 6x2y
b, 3x – 3y + x2 – y2
c, x3 + 4x2 + 4x – xy2
d. Tìm x biết x3 – 4x = 0
\(a,=3xy\left(x-2y\right)\\ b,=3\left(x-y\right)+\left(x-y\right)\left(x+y\right)=\left(x+y+3\right)\left(x-y\right)\\ c,=x\left[\left(x+2\right)^2-y^2\right]=x\left(x+y+2\right)\left(x-y+2\right)\\ d,\Leftrightarrow x\left(x^2-4\right)=0\Leftrightarrow x\left(x-2\right)\left(x+2\right)=0\Leftrightarrow\left[{}\begin{matrix}x=0\\x=2\\x=-2\end{matrix}\right.\)
Đúng 1
Bình luận (0)
Tìm x biết:a)
x
6
+ 2
x
3
+1 0; b) x(x - 5) 4x - 20;c)
x
4
-2
x
2
8-4
x
2
; d) (
x
3
-
x
2
) - 4
x
2
+ 8x-4 0.
Đọc tiếp
Tìm x biết:
a) x 6 + 2 x 3 +1 = 0; b) x(x - 5) = 4x - 20;
c) x 4 -2 x 2 =8-4 x 2 ; d) ( x 3 - x 2 ) - 4 x 2 + 8x-4 = 0.
a) x = -1. b) x = 4 hoặc x = 5.
c) x = ± 2 . d) x = 1 hoặc x = 2.
Đúng 0
Bình luận (0)
Tìm x:
a) x4-25x3=0
b) (x-5)2-(3x-2)2=0
c) x3-4x2-9x+36=0
d) (-x3+3x2-4x) : (\(-\dfrac{1}{2}\)x)=0
a.
$x^4-25x^3=0$
$\Leftrightarrow x^3(x-25)=0$
\(\Leftrightarrow \left[\begin{matrix} x^3=0\\ x-25=0\end{matrix}\right.\Leftrightarrow \left[\begin{matrix} x=0\\ x=25\end{matrix}\right.\)
b.
$(x-5)^2-(3x-2)^2=0$
$\Leftrightarrow (x-5-3x+2)(x-5+3x-2)=0$
$\Leftrightarrow (-2x-3)(4x-7)=0$
\(\Leftrightarrow \left[\begin{matrix}
-2x-3=0\\
4x-7=0\end{matrix}\right.\Leftrightarrow \left[\begin{matrix}
x=\frac{-3}{2}\\
x=\frac{7}{4}\end{matrix}\right.\)
Đúng 1
Bình luận (0)
c.
$x^3-4x^2-9x+36=0$
$\Leftrightarrow x^2(x-4)-9(x-4)=0$
$\Leftrightarrow (x-4)(x^2-9)=0$
$\Leftrightarrow (x-4)(x-3)(x+3)=0$
\(\Leftrightarrow \left[\begin{matrix} x-4=0\\ x-3=0\\ x+3=0\end{matrix}\right.\Leftrightarrow \left[\begin{matrix} x=4\\ x=3\\ x=-3\end{matrix}\right.\)
d. ĐK: $x\neq 0$
$(-x^3+3x^2-4x):(\frac{-1}{2}x)=0$
$\Leftrightarrow x(-x^2+3x-4):(\frac{-1}{2}x)=0$
$\Leftrightarrow -2(-x^2+3x-4)=0$
$\Leftrightarrow x^2-3x+4=0$
$\Leftrightarrow (x-1,5)^2=-1,75< 0$ (vô lý)
Vậy pt vô nghiệm.
Đúng 1
Bình luận (0)
Xem thêm câu trả lời
Tìm x
a) 4x(x + 1) = 8(x + 1)
b) x(x – 1) – 2(1 – x) = 0
c) 5x(x – 2) – (2 – x) = 0
d) 5x(x – 200) – x + 200 = 0
e) x3 + 4x = 0
f) (x + 1) = (x + 1)2
a) 4x(x+1)=8(x+1)
<=>4x(x+1)-8(x+1)=0
<=>(4x-8)(x+1)=0
<=>\(\left[\begin{array}{} 4x-8=0\\ x+1=0 \end{array} \right.\)
<=>\(\left[\begin{array}{} x=2\\ x=-1 \end{array} \right.\)
Vậy...
b)x(x-1)-2(1-x)=0
<=>(x+2)(x-1)=0
<=>\(\left[\begin{array}{} x+2=0\\ x-1=0 \end{array} \right.\)
<=>\(\left[\begin{array}{} x=-2\\ x=1 \end{array} \right.\)
Vậy...
c)5x(x-2)-(2-x)=0
<=>(5x+1)(x-2)=0
<=>\(\left[\begin{array}{} 5x+1=0\\ x-2 \end{array} \right.\)
<=>\(\left[\begin{array}{} x=-1/5\\ x=2 \end{array} \right.\)
d)5x(x-200)-x+200=0
<=>(5x-1)(x-200)=0
<=>\(\left[\begin{array}{} 5x-1=0\\ x-200=0 \end{array} \right.\)
<=>\(\left[\begin{array}{} x=1/5\\ x=200 \end{array} \right.\)
e)\(x^3+4x=0 \)
\(\Leftrightarrow x(x^2+4)=0 \)
\(\Leftrightarrow \left[\begin{array}{} x=0\\ x^2+4=0 (loại vì x^2+4>=0 với mọi x) \end{array} \right.\)
Vậy x=0
f)\((x+1)=(x+1)^2\)
\(\Leftrightarrow (x+1)-(x+1)^2=0\)
\(\Leftrightarrow (x+1)(1-x-1)=0\)
\(\Leftrightarrow (x+1)(-x)=0\)
\(\Leftrightarrow \left[\begin{array}{} x=-1\\ x=0 \end{array} \right.\)
Vậy....
Đúng 1
Bình luận (0)
Bài 5. Tìm x, biết:
a) x (2x - 7) + 4x -14 = 0
b) x3 - 9x = 0
c) 4x2 -1 - 2(2x -1)2 = 0
d) (x3 - x2 ) - 4x2 + 8x - 4 = 0
\(a,\Leftrightarrow x\left(2x-7\right)+2\left(2x-7\right)=0\\ \Leftrightarrow\left(x+2\right)\left(2x-7\right)=0\Leftrightarrow\left[{}\begin{matrix}x=-2\\x=\dfrac{7}{2}\end{matrix}\right.\\ b,\Leftrightarrow x\left(x^2-9\right)=0\\ \Leftrightarrow x\left(x-3\right)\left(x+3\right)=0\Leftrightarrow\left[{}\begin{matrix}x=0\\x=3\\x=-3\end{matrix}\right.\\ c,\Leftrightarrow\left(2x-1\right)\left(2x+1\right)-2\left(2x-1\right)^2=0\\ \Leftrightarrow\left(2x-1\right)\left(2x+1-4x+2\right)=0\\ \Leftrightarrow\left(2x-1\right)\left(-2x+3\right)=0\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{1}{2}\\x=\dfrac{3}{2}\end{matrix}\right.\\ d,\Leftrightarrow x^2\left(x-1\right)-4\left(x-1\right)^2=0\\ \Leftrightarrow\left(x-1\right)\left(x^2-4x+4\right)=0\\ \Leftrightarrow\left(x-1\right)\left(x-2\right)^2=0\Leftrightarrow\left[{}\begin{matrix}x=1\\x=2\end{matrix}\right.\)
Đúng 3
Bình luận (0)