Phương trình đường thẳng d: y = kx − 3

Phương trình hoành độ giao điểm của (P) và  d : - x 2 + 4 x - 3 = k x - 3

⇔ - x 2 + 4 - k x = 0 ⇔ x - x + 4 - k = 0 1

d cắt đồ thị (P) tại 2 điểm phân biệt khi (1) có 2 nghiệm phân biệt ⇔ 4 - k ≠ 0 ⇔ k ≠ 4

Ta có E x 1 ; k x 1 − 3 ,   F x 2 ; k x 2 − 3 với x 1 ,   x 2 là nghiệm phương trình (1)

Δ O E F  vuông tại O ⇒ O E → .   O F → = 0 ⇔ x 1 . x 2 + k x 1 − 3 k x 2 − 3 = 0

⇔ x 1 . x 2 1 + k 2 − 3 k x 1 + x 2 + 9 = 0 ⇔ 0. 1 + k 2 − 3 k ( 4 − k ) + 9 = 0

⇔ k 2 − 4 k + 3 = 0 ⇔ k = 1 k = 3

Đáp án cần chọn là: D

Đường thẳng d đi qua A và có hệ số góc k nên có dạng y= k( x+ 1)   hay

Kx- y+k=0 .

Phương trình hoành độ giao điểm của C  và  d là:

x 3 - 3 x 2 + 4 = k x + k ⇔ ( x + 1 ) ( x 2 - 4 x + 4 - k ) = 0

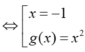
D cắt tại ba điểm phân biệt khi phương trình (*) có hai nghiệm phân biệt khác -1

⇔ ∆ ' > 0 g ( - 1 ) ≠ 0 ⇔ k > 0 k ≠   9

Khi đó g( x) =0 khi x=2- k ;   x = 2 + k    Vậy các giao điểm của hai đồ thị lần lượt là

A ( - 1 ;   0 ) ; B ( 2 - k ;   3 k - k k ) ; C ( 2 + k ;   3 k + k k ) .

Tính được

B C = 2 k 1 + k 2 , d ( O , B C ) = d ( O , d ) = k 1 + k 2 .

Khi đó 

S ∆ O B C = 1 2 . k k 2 + 1 . 2 k . k 2 + 1 = 1 ⇔ k k = 1 ⇔ k 3 = 1 ⇔ k = 1 .

Vậy k= 1 thỏa yêu cầu bài toán.

Chọn C.

Đường thẳng (d) có dạng \(y=kx+m\)

\(A\left(0;2\right)\in\left(d\right)\Rightarrow m=2\)

\(\Rightarrow y=kx+2\left(d\right)\)

\(\left(d\right)\) cắt \(\left(P\right)\) tại hai điểm phân biệt khi phương trình \(x^2+\left(4-k\right)x+1=0\) có hai nghiệm phân biệt

\(\Leftrightarrow\Delta=\left(k-2\right)\left(k-6\right)>0\)

\(\Leftrightarrow\left[{}\begin{matrix}k>6\\k< 2\end{matrix}\right.\)

Ta có \(x_1=\dfrac{k-4+\sqrt{k^2-8k+12}}{2}\Rightarrow y_1=\dfrac{k^2-4k+4+k\sqrt{k^2-8k+12}}{2}\)

\(\Rightarrow E\left(\dfrac{k-4+\sqrt{k^2-8k+12}}{2};\dfrac{k^2-4k+4+k\sqrt{k^2-8k+12}}{2}\right)\)

\(x_1=\dfrac{k-4-\sqrt{k^2-8k+12}}{2}\Rightarrow y_1=\dfrac{k^2-4k+4-k\sqrt{k^2-8k+12}}{2}\)

\(\Rightarrow F\left(\dfrac{k-4-\sqrt{k^2-8k+12}}{2};\dfrac{k^2-4k+4-k\sqrt{k^2-8k+12}}{2}\right)\)

Tọa độ trung điểm \(I\left(\dfrac{k-4}{2};\dfrac{k^2-4k+4}{2}\right)\)

\(x-2y+3=0\left(d'\right)\)

\(I\left(\dfrac{k-4}{2};\dfrac{k^2-4k+4}{2}\right)\in\left(d'\right)\Rightarrow\dfrac{k-4}{2}-\left(k^2-4k+4\right)+3=0\)

\(\Leftrightarrow2k^2-9k+6=0\)

\(\Leftrightarrow\left[{}\begin{matrix}k=\dfrac{9+\sqrt{33}}{2}\left(l\right)\\k=\dfrac{9-\sqrt{33}}{2}\left(tm\right)\end{matrix}\right.\)

\(\Leftrightarrow k=\dfrac{9-\sqrt{33}}{2}\)

P/s: Không biết đúng kh.

tự làm

a: Hệ số góc là a=2

Tung độ góc là b=2

c: Thay x=3 vào y=2x+2, ta được:

y=2x3+2=8

Vậy: A(3;8) có thuộc (d)