Giải phương trình sau và biểu diễn tập nghiệm trên trục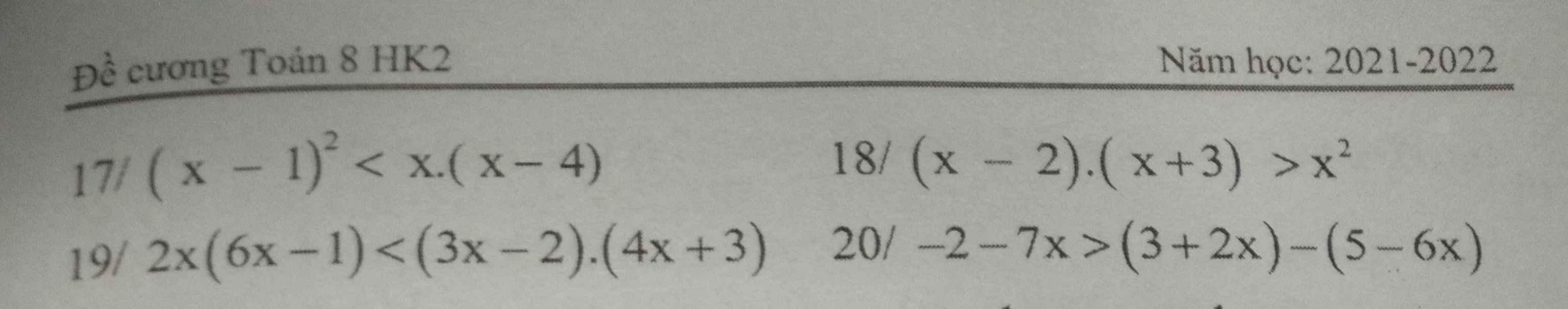

Những câu hỏi liên quan
Giải các bất phương trình sau và biểu diễn tập nghiệm trên trục số:
x^2<9
Ta có: \(x^2< 9\)
\(\Leftrightarrow\left\{{}\begin{matrix}-3< x\\x< 3\end{matrix}\right.\Leftrightarrow-3< x< 3\)
Đúng 1
Bình luận (1)
giải bất phương trình sau và biểu diễn tập nghiệm trên trục số x + 3 > 6
\(x+3>6\)
\(\Leftrightarrow x>6-3\)
\(\Leftrightarrow x>3\)
Biểu diễn trên trục số:
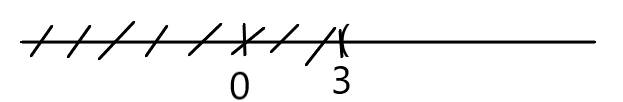
Đúng 0
Bình luận (0)
Giải phương trình sau và biểu diễn tập nghiệm trên trục
GIÚP EM VỚI PLEASE 😢😭😭
\(\dfrac{3x-1}{4}>2\)
\(\Leftrightarrow\dfrac{3x-1}{4}-2>0\)
\(\Leftrightarrow3x-1-8>0\)
\(\Leftrightarrow3x-9>0\)
\(\Leftrightarrow3x>9\)
\(\Leftrightarrow x>3\)
Vậy \(S=\left\{x|x>3\right\}\)
Đúng 1
Bình luận (0)
giải bất phương trình sau và biểu diễn tập hợp nghiệm trên trục số
Giải các bất phương trình sau và biểu diễn tập nghiệm trên trục số: a, 3x -11 >5 -x
\(a,3x-11>5-x\\ \Leftrightarrow3x+x>5+11\\ \Leftrightarrow4x< 16\\ \Leftrightarrow x>4\)
Vậy bất phương trình có nghiệm là: \(S=\left\{x|x>4\right\}\)
biểu diễn
Đúng 1
Bình luận (0)
Bài 2: ( 1 điểm) Giải bất phương trình sau và biểu diễn tập nghiệm trên trục số. 3x + 5 - 1
Giải bất phương trình sau đây và biểu diễn tập nghiệm trên trục số : x - 1 3 - 3 x + 5 2 ≥ 1 - 4 x + 5 6
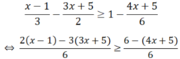
⇔ 2x - 2 - 9x - 15 ≥ 6 - 4x - 5
⇔ 2x - 9x + 4x ≥ 6 - 5 + 2 + 15
⇔ -3x ≥ 18
⇔ x ≤ -6
Vậy tập nghiệm của phương trình là S= {x|x ≤ -6}
Biểu diễn nghiệm trên trục số:
![]()
Đúng 0
Bình luận (0)
giải các bất phương trình sau và biểu diễn tập nghiệm trên trục số
a) 2x-8≥≥0.
b)10+10x>0
Giải các bất phương trình và biểu diễn tập nghiệm trên trục số:
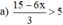
⇔ 15 – 6x > 15 (Nhân cả hai vế với 3 > 0, BPT không đổi chiều)
⇔ -6x > 15 – 15 (Chuyển vế và đổi dấu hạng tử 15)
⇔ -6x > 0
⇔ x < 0 (Chia cả hai vế với -6 < 0, BPT đổi chiều)
Vậy nghiệm của bất phương trình là x < 0.

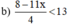
⇔ 8 – 11x < 13.4 (Nhân cả hai vế với 4 > 0, BPT không đổi chiều)
⇔ 8 – 11x < 52
⇔ -11x < 52 – 8 (Chuyển vế và đổi dấu hạng tử 8)
⇔ -11x < 44
⇔ x > 44 : (-11) (Chia cả hai vế cho -11 < 0, BPT đổi chiều
⇔ x > -4.
Vậy bất phương trình có nghiệm x > -4.

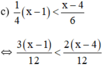
⇔ 3(x – 1) < 2(x – 4) (Nhân cả hai vế với 12 > 0, BPT không đổi chiều)
⇔ 3x – 3 < 2x – 8
⇔ 3x – 2x < -8 + 3 (Chuyển vế và đổi dấu 2x và -3)
⇔ x < -5
Vậy bất phương trình có tập nghiệm x < -5.

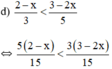
⇔ 5(2 – x) < 3(3 – 2x) (Nhân cả hai vế với 15 > 0, BPT không đổi chiều)
⇔ 10 – 5x < 9 – 6x
⇔ 6x – 5x < 9 – 10 (Chuyển vế và đổi dấu -6x và 10)
⇔ x < -1.
Vậy bất phương trình có tập nghiệm x < -1.

Đúng 0
Bình luận (0)




















