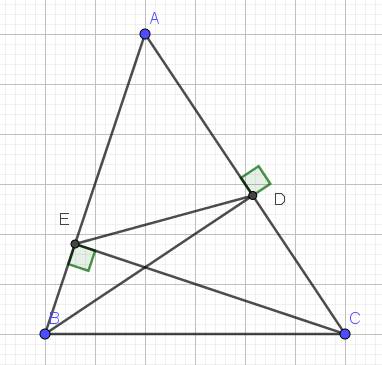
cho tam giác ABC đều , 2 đường cao BD và CE . a : chứng minh 4 điểm B;C;D;E cùng thuộc 1 đường tròn b: Gọi G là giao điểm của BD và CE . Chứng minh : 4 điểm A , E , D , G cùng thuộc 1 đường tròn . Tính Bán kính của đường tròn biết AB = 8 cm

Những câu hỏi liên quan
cho tam giác ABC nhọn, BD là đường trung tuyến, CE là đường cao. Sao cho BD = CE và góc BDC = góc ECA. BD cắt CE tại H. Chứng minh a) HE*HC = HB*HD
b) chứng minh tam giác ABC đều
Cho tam giác ABC đường cao BD và CE A) gọi y là giao điểm của BD và CE. Chứng minh 4 điểm BD CE cùng nằm trên 1 đường tròn
Lời giải:
Xét tứ giác $BEDC$ có:
$\widehat{BEC}=\widehat{BDC}=90^0$. Mà 2 góc này cùng nhìn cạnh $BC$ nên $BEDC$ là tứ giác nội tiếp.
$\Rightarrow B,C,E,D$ cùng nằm trên 1 đường tròn.
Đúng 0
Bình luận (0)
Cho tam giác ABC nhọn có ba đường cao AK,BD,CE a. Chứng minh rằng: tam giác ABC ~ tam giác ACE b. Gọi H là giao điểm của AK, BD, CE. Chứng minh rằng :CH. CE=BC.CK c. Chứng minh rằng: BH. BD+CH. CE=BC^2
a: Xét ΔABD vuông tại D và ΔACE vuông tại E có
góc CAE chung
Do đó; ΔABD đồng dạng với ΔACE
b: Xét ΔCKH vuông tại K và ΔCEB vuông tại E có
góc ECK chung
Do đó: ΔCKH\(\sim\)ΔCEB
Suy ra: CK/CE=CH/CB
hay \(CH\cdot CE=CB\cdot CK\)
Đúng 0
Bình luận (0)
Bài 2 : Cho tam giác ABC có 2 đường cao BD và CE
a, Chứng minh : tam giác ABD đồng dạng với tam giác ACE
b, Chứng minh tam giác ADE đồng dạng với tam giác ABC c , Gọi H là giao điểm của BD và CE , K là giao điểm của BD và CE
K là giao điểm của AH và BC
Chứng minh rằng : AH vuông góc với BC và CH*CE=BC*CK
d, Chứng minh rằng BH*BD+CH*CE=BC2
Cho tam giác ABC có góc A = 60 độ, đường cao BD và CE. Gọi M là trung điểm BC. Chứng minh tam giác MDE đều
cho tam giác ABC có ba góc đều nhọn nội tiếp đường tròn O hai đường cao BD và CE cắt đường tròn O theo thứ tự P vs Q
a, chứng minh tứ giác BCDE nội tiếp đường tròn
b, gọi H là giao điểm của BD và CE, chứng minh HB.HP=HC.HQ
c, chứng minh OA vuông góc với DE
VẼ HÌNH GIÚP MÌNH VỚI NHA!
a: góc BEC=góc BDC=90 độ
=>BEDC nội tiếp
b: Xét ΔHQB và ΔHPC có
góc HQB=góc HPC
góc QHB=góc PHC
=>ΔHQB đồng dạng với ΔHPC
=>HQ/HP=HB/HC
=>HQ*HC=HP*HB
c: kẻ tiếp tuyến Ax
=>góc xAC=góc ABC=góc ADE
=>Ax//ED
=>OA vuông góc DE
Đúng 0
Bình luận (0)
Cho tam giác ABC cân tại a có BD và CE là các đường cao a) chứng minh tam giác ABD = tam giác ACE và tam giác BDC = tam giác CEB b) gọi h là giao điểm của BD và CE .chứng minh AH đi qua trung điểm của BC
a) Xét ΔABD vuông tại D và ΔACE vuông tại E có
AB=AC(ΔABC cân tại A)
\(\widehat{BAD}\) chung
Do đó: ΔABD=ΔACE(cạnh huyền-góc nhọn)
Xét ΔBDC vuông tại D và ΔCEB vuông tại E có
BC chung
BD=CE(ΔABD=ΔACE)
Do đó: ΔBDC=ΔCEB(cạnh huyền-cạnh góc vuông)
Đúng 0
Bình luận (0)
Cho tam giác ABC đều có cạnh = a, các đường cao BD và CE cắt nhau tại H
a) Chứng minh: 4 điểm B,E,D,C thuộc cùng 1 đường tròn. Hãy xác định tâm và bán kính của đường tròn ấy
b) Chứng minh: Điểm H nắm trong đường tròn và điểm A nằm ngoài đường tròn đi qua 4 điểm B,E,D,C
a: Xét tứ giác BEDC có
\(\widehat{BEC}=\widehat{BDC}=90^0\)
Do đó: BEDC là tứ giác nội tiếp
Tâm là trung điểm của BC
Bán kính là \(\dfrac{BC}{2}=\dfrac{a}{2}\)
Đúng 0
Bình luận (0)
cho tam giác ABC có các góc đều nhọn. A=45 độ. vẽ các đương cao BD và Ce của tam giác ABC. gọi H là giao điểm của BD và CE
a/ chứng minh tứ giác ADHE nội tiếp
b/ chứng minh HD=DC
c/ gọi o là tâm đường tròn ngoại tiếp tam giác ABC. chưng minh OA vuong góc với DE












